高速铁路板式无砟轨道的结构分析模型对比

孙 璐 段雨芬 高培培

(1东南大学交通学院,南京210096)(2美国天主教大学土木工程系,华盛顿20064)

轨道结构作为高速铁路工程结构的上部结构,直接承受列车荷载并将荷载传递至线下基础结构,其力学特性直接关系到线下基础结构的受力以及列车行驶的舒适性和安全性.传统的有砟轨道分析方法经过一百多年的发展已经趋于成熟,而关于无砟轨道结构的研究尚不成熟.板式无砟轨道作为一种新型的无砟轨道结构,在我国快速形成的高速铁路网中得到了广泛的应用,但是由于高速铁路在我国尚处于起步阶段,对于板式无砟轨道结构,尚未得到统一的分析理论[1].翟婉明等[2]将板式无砟轨道作为2层梁体系进行分析研究,发展了车辆-轨道耦合动力学;向俊等[3-4]针对板式轨道结构特点,提出了一种横向有限条与无砟轨道板段单元分析模型.马学宁[5]在研究板式无砟轨道时将钢轨离散成梁单元,垫板和扣件采用弹簧-阻尼单元模拟,轨道板、水泥乳化沥青砂浆层、钢筋混凝土底座及以下介质(包括路基)均离散成四边形单元.罗震等[6]采用有限元方法建立了板式轨道结构力学分析模型.

现有研究中,研究者们往往是在车辆轨道整体研究的基础上选用一种已有的轨道结构理论,而专门针对无砟轨道结构理论进行的研究相对较少.本文根据我国高铁无砟轨道自身的特点,对CRTS Ⅱ和CRTS Ⅲ型板式无砟轨道的结构力学理论进行研究.

1 无砟轨道力学理论模型

传统轨道结构的力学分析理论以弹性基础梁理论为主,假设钢轨为置放在弹性基础上的连续梁.采用传统的轨道力学理论对板式无砟轨道结构进行受力分析时,将其视为受集中力作用的无限长连续支承梁[7-8](见图1).在集中荷载作用处建立局部坐标系,取钢轨纵向为x轴正方向,竖直向下为y轴正方向;P0为钢轨所承受的上部荷载;y为P0作用下钢轨的挠度.

图1 集中力作用的无限长梁

根据Winkler假设,结合材料力学基本公式及集中荷载作用下无限长梁的边界条件,计算得轨道钢轨的挠度y和弯矩M分别为

(1)

(2)

1.1 弹性地基叠合梁理论

弹性地基叠合梁理论是在传统轨道力学弹性地基梁理论的基础上结合无砟轨道结构特点提出的.无砟轨道结构主要由轨道板、扣件、CA砂浆、混凝土底座(或支承层)等构件组成.根据对称性,将无砟轨道结构分别从纵向板中截面和横向板中截面进行剖开,无砟轨道结构可以看成是由多根梁叠合而成.弹性地基叠合梁理论正是基于这种思想,忽略结构横向和纵向的协调变形关系,从结构纵向和横向分别进行计算[9-10].

轨道结构纵向可以视为弹性地基上的三重叠合梁,CA砂浆层等效为弹簧连接,下部基础设施采用等效Winkler地基模型,纵向力学分析模型如图2所示.根据纵向力学分析模型计算得到最大钢轨压力,将列车竖向荷载等效为作用在轨道板上的均布荷载,其他结构层的等效模型与纵向力学分析模型类似,由此可得横向力学分析模型(见图3).图中,P为施加的荷载；q为反力；E1,E2,E3分别为钢轨、轨道板、底座(或支承层)的弹性模量纵向抗弯刚度;I1,I2,I3分别为钢轨、轨道板、底座(或支承层)的截面惯性矩;I4,I5分别为轨道板和底座(或支承层)的横向截面惯性矩;x20,x11,x12,x13分别为L0，L1,L2,L3区段内钢轨的纵向位移;x21,x22,x23分别为L1,L2,L3区段内轨道板的纵向位移;x31,x32,x33分别为L1,L2,L3区段内底座(或支承层)的纵向位移;y11,y12,y13分别为L1,L2,L3区段内钢轨的挠度;y20，y21,y22,y23分别为L0，L1,L2,L3区段内轨道板的挠度;y31,y32,y33分别为L1,L2,L3区段内底座(或支承层)的挠度;k1,k2,k3分别为钢轨、轨道板、底座(或支承层)单位长度内的纵向支承弹性系数;k4,k5分别为轨道板和底座(或支承层)单位长度内的横向支承弹性系数.

基于弹性地基叠合梁理论分析模型,可求出无砟轨道在纵向和横向方向上各部件截面的挠度变形.再根据力学微小变形原理,对挠度y求导,便可得各梁的转角θ、弯矩M、剪力Q和反力q的函数关系为

图3 弹性地基叠合梁横向分析模型

(3)

1.2 弹性地基梁-板理论

无砟轨道各结构层在厚度方向上的尺寸远小于其他2个方向的尺寸，且荷载作用下的挠度远小于其厚度.鉴于此，在分析模型中，轨道板和混凝土底座(或支承层)采用板壳单元进行模拟；扣件、CA砂浆层和填充层采用弹簧单元进行模拟；下部基础采用Winkler弹性地基模型进行模拟.考虑到钢轨属于细长结构，采用弹性点支承梁单元对钢轨进行模拟(见图4)[11-12].图中,ER,ES,EU分别为R梁、S板、U板的弹性模量纵向抗弯刚度;IR,IS,IU分别为R梁、S板、U板的截面惯性矩;kCA,kRD,kZ分别为CA层、RD层、Z层的弹性系数.

图4 无砟轨道结构的弹性地基梁-板模型

1.3 梁-体有限元理论

在无砟轨道梁-体有限元理论中，将无砟轨道结构离散成有限单元，各单元通过变形连续条件和力的平衡条件连接，建立轨道结构的空间分析模型.在分析模型中，钢轨采用弹性点支承梁单元进行模拟；扣件采用线性弹簧单元或连接单元进行模拟；轨道板、CA砂浆层(或填充层)、混凝土底座(或支承层)及线下基础结构(路基、桥梁)采用实体单元进行模拟，其几何尺寸和材料参数按结构实际参数取值[13].

2 数值算法

采用弹性地基叠合梁理论分析模型对无砟轨道结构进行分析时,应用半解析法进行位移和弯矩计算,利用Matlab微分方程求解器的功能对微分方程进行求解;对于弹性地基梁-板理论分析模型和梁-体有限元理论分析模型,运用ABAQUS有限元软件建立具体分析模型,进行无砟轨道各结构层的位移和弯矩计算[14].将京沪高速铁路上所铺设的CRTS Ⅱ型以及武黄城际铁路上铺设的CRTS Ⅲ型板式无砟轨道结构作为有限元基准模型,计算过程中的轨道结构和线下基础结构的材料参数分别见表1和表2.

为了消除边界效应,在板式无砟轨道结构分析模型中,选取3块单元轨道板进行计算,以中间单元板作为研究对象.图5为梁-体有限元理论分析模型.

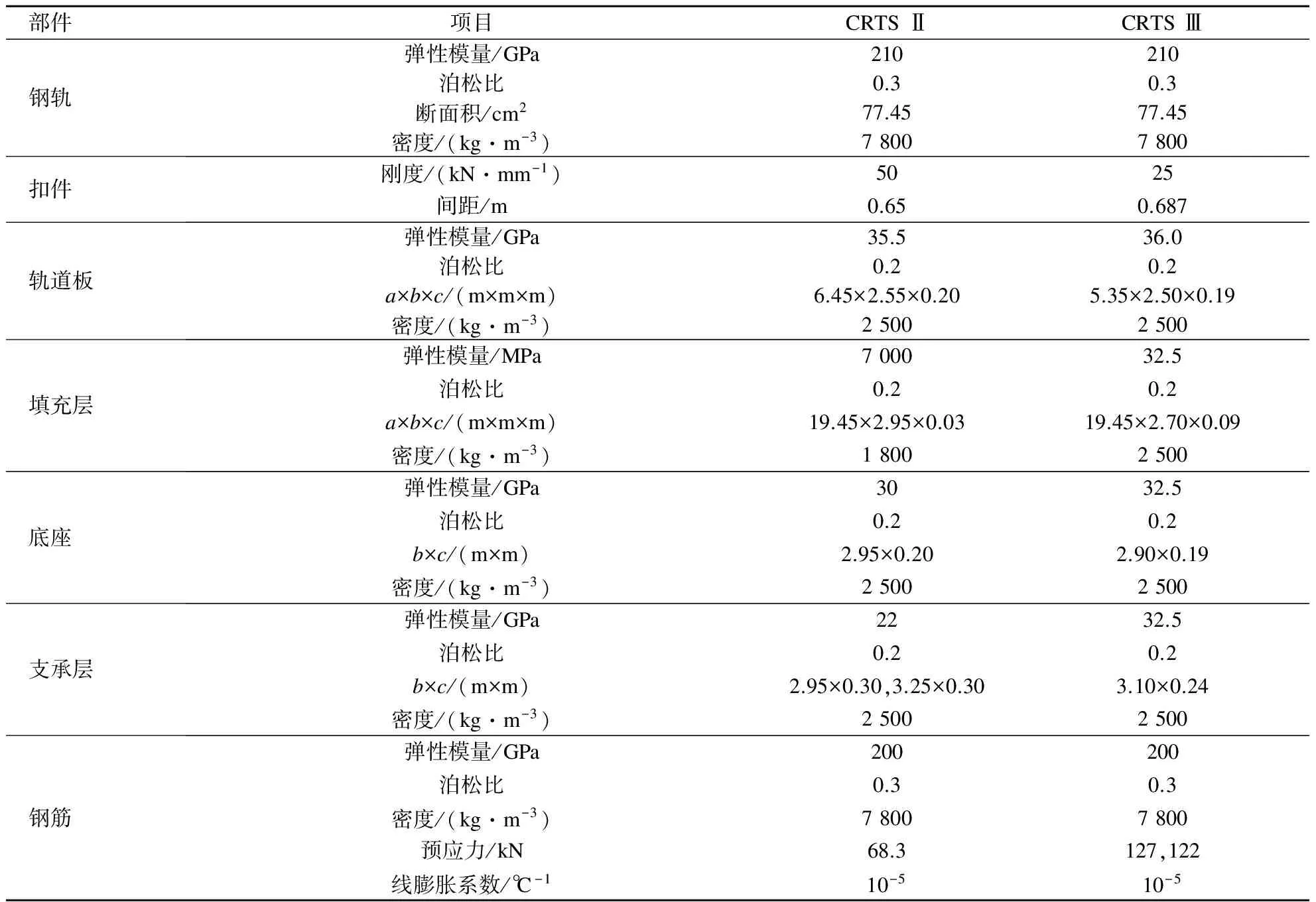
表1 板式无砟轨道结构模型的材料参数

表2 线下基础结构模型材料参数

图5 板式无砟轨道梁-体有限元分析模型

3 结果分析

利用3种理论分析模型计算得到不同线下基础结构上2种板式无砟轨道结构的竖向位移和弯矩,结果分别见表3和表4.

由表3和表4可知,对于钢轨而言,采用弹性地基叠合梁理论分析模型和梁-体有限元理论分析模型计算时,各力学指标相差不大;与弹性地基叠合梁理论分析模型和梁-体有限元理论分析模型的计算结果相比,采用弹性地基梁-板理论分析模型计算时,钢轨竖向位移偏大约30%,CRTS Ⅱ型板上钢轨弯矩计算值偏小约25%,CRTS Ⅲ型板上钢轨弯矩偏小约35%.

对于轨道结构而言,3种分析模型计算所得的竖向位移和横/纵向负弯矩相差不大,但正弯矩差异明显.相比于弹性地基叠合梁理论分析模型和梁-体有限元理论分析模型,采用弹性地基梁-板理论分析模型计算时,路基上CRTS Ⅱ和CRTS Ⅲ型板的纵向正弯矩计算值偏大约1倍,横向正弯矩偏大约23%；桥梁上CRTS Ⅱ和CRTS Ⅲ型板的纵向正弯矩计算值偏大约2倍,横向正弯矩偏大约20%.此外,采用弹性地基梁-板理论分析模型计算时,横向正/负弯矩均小于纵向正/负弯矩,这与另外2种理论的计算结果恰好相反,这是由于前者计算时横向仅取单个扣件间距范围内的结构进行分析,忽略了相邻范围内轨道结构对荷载的分担及约束.

表3 CRTS Ⅱ型板式无砟轨道结构的分析模型计算结果对比

表4 CRTS Ⅲ型板式无砟轨道结构的分析模型计算结果对比

对于底座(或支承层)而言,采用弹性地基叠合梁理论分析模型和弹性地基梁-板理论分析模型计算得到的竖向位移相差不大.相较于这2种分析模型的计算结果,采用梁-体有限元理论计算得到的竖向位移减小约50%.而弯矩计算结果与轨道版型有直接联系,对于CRTS Ⅱ型板,各弯矩指标差别不大;对于CRTS Ⅲ型板,采用3种理论分析模型计算路基上底座(或支承层)纵向正弯矩时,弹性地基梁-板理论分析模型计算得到的数值最大,较弹性地基叠合梁理论分析模型偏大约16%,较梁-体有限元理论分析模型偏大约44%.采用3种理论分析模型计算纵向负弯矩时，弹性地基叠合梁理论分析模型计算时得到的数值最大,较弹性地基梁-体理论分析模型偏大约7%,较梁-体有限元理论分析模型偏大约21%.采用弹性地基叠合梁理论分析模型和弹性地基梁-板理论分析模型计算横向正弯矩时，结果相差不大,均比采用梁-体有限元理论分析模型的计算结果偏小约13%.

采用3种理论分析模型计算桥梁上底座(或支承层)纵向正弯矩时,弹性地基梁-板理论分析模型时计算得到的数值最大,较弹性地基叠合梁理论分析模型偏大约171%,较梁-体有限元理论分析模型偏大约338%.采用3种理论分析模型计算横向正弯矩时,梁-体有限元理论分析模型计算得到的数值最大,较弹性地基叠合梁理论分析模型偏大约11%,较弹性地基梁-板理论分析模型偏大约13%.3种理论计算所得的纵向负弯矩相差不大.此外,路基上底座(或支承层)的弯矩值明显大于桥梁上底座(或支承层)的弯矩,这是由于路基的面支承刚度小于桥梁基础.

从工程应用角度而言,3种理论分析模型计算得到的结果均能满足工程设计要求.由于弹性地基叠合梁理论分析模型相对简单,且可以得到解析解,因而受到工程设计人员的青睐;然而,其模型纵向取半宽结构，横向取单个扣件范围内的结构,忽略了轨道结构整体的纵、横向变形协调,导致部分计算结果与实际情况存在一定差异.弹性地基梁-板理论分析模型能较好地模拟轨道板和底座(或支承层)的弯曲变形,计算结果较其他2种分析模型偏于安全.梁-体有限元理论分析模型可真实反映无砟轨道结构的受力和变形,但分析模型相对复杂,对工程设计人员要求较高,一般适用于无砟轨道结构的研发和设计验证.

4 结论

1) 采用3种理论分析模型计算不同线下基础结构上2种板式无砟轨道的结构受力时,基于弹性地基梁-板理论分析模型计算得到的钢轨竖向位移较其他2种分析模型的结果偏大约30%;利用弹性地基叠合梁理论模型计算得到的钢轨弯矩值较其他2种模型的结果大.

2) 采用3种理论分析模型计算得到的钢轨、轨道板和底座(或支承层)的正弯矩值均大于负弯矩值,即轨道板和底座(支承层)以板底受拉为主.

3) 弹性地基叠合梁理论分析模型相对简单,但计算结果需要进行适当修正;弹性地基梁-板理论分析模型可以较好地模拟轨道板和底座(或支承层)的弯曲变形,但相对其他2种分析模型计算结果偏大;梁-体有限元理论分析模型可以真实地反映无砟轨道结构的受力和变形,但分析模型相对复杂,一般适用于无砟轨道结构的研发和设计验证.

)

[1] 刘学毅,赵坪锐,杨荣山，等.客运专线无砟轨道设计理论与方法[M].成都:西南交通大学出版社,2010:9-11.

[2] 翟婉明,韩卫军.高速铁路板式轨道动力特性研究[J].铁道学报,1999,21(6): 64-69.

Zhai Wanming,Han Weijun.High speed railway slab track dynamic characteristics research[J].JournaloftheChinaRailwaySociety, 1999,21(6): 64-69.(in Chinese)

[3] 向俊,赫丹,曾庆元.横向有限条与无砟轨道板段单元的车轨系统竖向振动分析法[J].铁道学报,2007,29(4):64-69.

Xiang Jun,He Dan,Zeng Qingyuan.Analysis method of vertical vibration of train and ballastless track system with the lateral finite strip and slab segment element[J].JournaloftheChinaRailwaySociety,2007,29(4):64-69.(in Chinese)

[4] 向俊,曹晔,刘保钢,等.客运专线板式无碴轨道动力设计参数[J]. 中南大学学报:自然科学版,2007,38(5): 981-986.

Xiang Jun,Cao Ye,Liu Baogang,et al.Dynamic parameters of slab track of passenger transport line[J].JournalofCentralSouthUniversity:ScienceandTechnlogy,2007,38(5): 981-986.(in Chinese)

[5] 马学宁.高速铁路板式无砟轨道-路基结构动力特性研究[J].铁道学报,2011,33(2):72-78.

Ma Xuening.Study on the dynamic properties of slab ballastless track and subgrade structure on high-speed railway[J].JournaloftheChinaRailwaySociety,2011,33(2):72-78.(in Chinese)

[6] 罗震,翟婉明,蔡成标.车辆作用下板式轨道动力分析模型及验证[J].铁道学报,2010,32(4):70-73.

Luo Zheng,Zhai Wanming,Cai Chengbiao.Dynamics model of slab track subjected to moving vehicle and its verification[J].JournaloftheChinaRailwaySociety,2010,32(4):70-73.(in Chinese)

[7] Ando K,Horiike T,Kubomura K,et al.Present status on slab track and environmental counter measure [J].QuarterlyReportofRTRI,1996,37(4): 204-209.

[8] Dinh V N,Kim K D,Warnitchai P.Dynamic analysis of three-dimensional bridge-high-speed train interactions using a wheel rail contact model[J].EngineeringStructure,2009,31(12):3090-3106.

[9] Tanabe M,Wakui H,Okuda H.Dynamic interaction analysis of an unlimited number of Shinkansen cars running on the railway track [J].VehicleSystemDynamics,2004,40(Sl): 91-106.

[10] 赵坪锐,章元爱,刘学毅，等.无砟轨道弹性地基梁板模型[J].中国铁道科学,2009,30(3):1-4.

Zhao Pingrui,Zhang Yuanai,Liu Xueyi, et al. Beam-plate model on the elastic foundation of ballastless track[J].ChinaRailwayScience, 2009,30(3):1-4.(in Chinese)

[11] Spengler M,Duda H,Graubner C A. Stress on railway bridges by high speed rail traffic: influence of the type of “Solid Track” superstrueture on the structural dynamic properties and the dynamic load bearing truss reaction [J].VDIBerichte,2006,28(19):731-746.(in German)

[12] 徐庆元,李斌,周小林.高速列车作用下路基上板式无砟轨道动力系数[J].中南大学学报:自然科学版,2011,42(9):2831-2836.

Xu Qingyuan,Li Bin,Zhou Xiaolin.Dynamic coeffcient of slab track system on subgrade under high speed trains[J].JournalofCentralSouthUniversity:ScienceandTechnology,2011,42(9):2831-2836.(in Chinese)

[13] 娄平, 曾庆元.移动荷载作用下板式轨道的有限元分析[J].交通运输工程学报,2004,4(1): 29-33.

Lou Ping,Zeng Qingyuan.Finite element analysis of slab track subjected to moving load[J].JournalofTrafficandTransportationEngineering, 2004,4(1): 29-33.(in Chinese)

[14] Hibbitt K, Sorenson I.ABAQUSanalysisuser’smanual,version6.10[M].Providence Rhode Island,USA: ABAQUS Inc., 2010.