基于实测数据的润扬大桥悬索桥全寿命评估随机温度场模拟

周广东 李爱群 丁幼亮 王高新

(1东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)(2河海大学土木与交通学院, 南京 210098)

扁平钢箱梁具有整体性强、自重轻、刚度大、工厂化程度高等优点,逐渐成为大跨度桥梁主梁的主要结构形式．然而,由于钢材的热膨胀系数高、导热性能好,太阳辐射的不均匀性以及大气温度骤然变化引起的温度梯度应力对钢桥的影响十分显著.理论分析和实验研究均表明,超静定桥梁结构体系中的温度应力可以达到甚至超过汽车活载的应力[1]．因此,对桥梁结构的温度场及其应力分析是桥梁结构全寿命评估的重要内容．

对桥梁进行温度应力分析,合理的结构温度场取值是前提．目前,针对桥梁结构温度场的研究主要有3种方法:① 现场实测.文献[2-6]对混凝土箱梁桥或钢-混凝土组合箱梁的横截面温度场进行了现场实测,并获得了箱梁温度场分布的一些规律．② 理论分析．Mirambell等[7]利用热传导方程推导了混凝土箱梁的竖向温度场分布;葛耀君等[8]利用傅里叶热传导理论,建立了混凝土斜拉桥温度场计算的二维差分方法．③ 数值模拟．Tong等[9]编制了二维有限元程序,以模拟钢桥温度场,并将模拟结果与实测结果进行对比;孙国晨等[10]对一座钢-混凝土叠合梁桥在日照作用下的温度分布进行了时程仿真分析．在这3种方法中,现场实测最为准确,但不能满足全寿命评估对温度数据的需求;理论计算难度大,往往需要对实际情况进行简化,计算结果与实际情况存在一定的差距;数值模拟结果在很大程度上依赖于输入参数的取值,故无法准确反映实际桥梁结构内的温度场．综合现场实测和数值模拟的优点,利用现场实测数据的统计规律进行数值模拟,不仅能够反映实际桥梁的温度分布,还能弥补桥梁全寿命评估温度数据的不足;这是一种较好的解决方法,但目前未见报道．

鉴于此,本文提出了一种基于桥梁结构长期实测数据统计规律的温度场模拟方法．首先,根据润扬大桥悬索桥扁平钢箱梁的长期实测温度数据,建立扁平钢箱梁不同测点的温度以及不同测点与参考点之间温差的统计模型;进而利用数值逆变换抽样方法,模拟得出实测概率分布模型下的温度和温差样本序列;最后,建立扁平钢箱梁横截面的温度场．此方法可以根据需要,生成不同长度且符合钢箱梁桥实际温度场统计特征的全寿命评估随机温度场,为钢箱梁桥的全寿命评估奠定基础．

1 润扬大桥悬索桥温度监测子系统

润扬大桥悬索桥为主跨1490m的单跨双铰简支钢箱梁桥．钢箱梁全宽为38.7m,高3.0m．图1为润扬大桥悬索桥钢箱梁横截面温度监测传感器的布置示意图,重点对扁平钢箱梁顶板和底板的温度进行实时监测．图中,S1～S8为测点．5年多的使用表明,温度传感器性能稳定,能够对扁平钢箱梁的温度场进行精确测量．本文以跨中截面的温度监测结果作为研究对象进行分析．

图1 润扬大桥悬索桥横截面温度传感器布置图

2 实测温度的统计特性分析

图2为典型测点S7一年内的温度时程曲线．从图中可以看出,钢箱梁的温度变化具有典型的季节性:冬季温度较低,夏季温度较高．根据文献[11],通过对多个概率分布模型的拟合优度进行比较,最终选用2个正态分布的加权和来描述润扬大桥悬索桥扁平钢箱梁横截面长期监测温度数据的统计特性．此模型可表示为

(1)

式中,T为测点温度;f(T)为监测温度的概率密度函数;N1(σ1,μ1)和N2(σ2,μ2)为正态分布,其中,σ1,μ1,σ2,μ2为正态分布的待定参数;α和β为权重系数,且α+β=1．

利用参数估计,得出测点S7的温度概率密度函数,并与实测概率密度进行对比,结果见图3．从图中可以看出,估计的概率密度曲线与实测概率密度曲线具有良好的一致性,表明估计的概率密度函数能够准确反映测点处不同温度出现的概率．跨中截面所有测点温度的概率密度函数见表1,表中结果均能通过显著性水平为0.05的K-S检验．由表可知,顶板处于对称位置测点的温度概率密度函数十分接近,因此,可以认为S1与S5,S2与S4的温度分布相同,S6,S7,S8的温度分布相同．

表1 扁平钢箱梁上不同测点温度的概率密度函数

3 实测温差的统计特性分析

扁平钢箱梁是一个具有无限自由度的超静定结构,横截面的温度应力分布与其上各点之间的温差直接相关,因此还需要考虑不同测点之间温差的统计特性．通过分析比较,利用1个Weibull分布和1个正态分布的加权和来估计横截面测点之间温差的概率密度函数,即

(2)

式中,Tij=Ti-Tj为不同测点之间的温差,其中i,j=1,2,…,8,且i≠j;W(a,b)为Weibull分布函数;N(σ,μ)为正态分布函数,其中a,b,σ,μ为待定参数．由于Weibull分布只能描述正随机变量的分布,故首先在温差值上加上一个正数(此处取3),使温差值全部变成正数．

以测点S2为参考点,利用式(2)分别估计温差T21,T23和T27的概率密度函数,结果见表2．表中结果均能通过显著性水平为0.05的K-S检验．

另外，今年还新增了“最佳格鲁吉亚葡萄酒”奖杯项目，由Château Mukhrani Réserve Royale Red 获得。东欧的另一焦点地区是捷克共和国，今年无论是参赛或得奖数目均有一倍的上升。

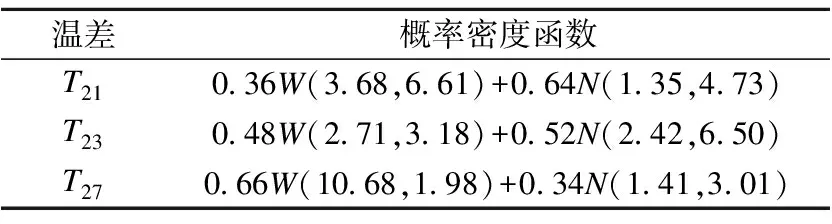
表2 温差的概率密度函数

4 随机温度场模拟

4.1 模拟方法

对某一概率密度函数下的样本序列进行模拟时,可以采用逆变换抽样方法．对于一个已知样本序列的随机变量X,假设其概率密度函数为f(x),另一个随机变量Y与X的关系为Y=Φ(X),则随机变量Y的概率分布函数为

(3)

令g(y)等于待模拟样本的概率密度函数,利用式(3)便可求出函数Φ(X)．在实际应用中,通常将随机变量X的概率分布取为均匀分布,利用X的已知样本即可求出服从概率密度函数g(y)的随机变量Y的样本序列．

采用逆变换抽样方法进行样本序列模拟的过程中,需要对目标概率密度函数g(y)进行积分和求反函数．扁平钢箱梁横截面温度场的概率密度函数较为复杂,无法得出其概率密度函数的积分和反函数的解析表达式．因此,本文根据逆变换抽样方法的思想,提出一种数值逆变换抽样方法．

设需要生成样本序列的总数为N,根据实测温度T的概率分布,采用极值分析法[12]得出需要生成的时间跨度范围内的最低温度Tmin和最高温度Tmax以及超过此范围的样本数N0,即随机温度的区间为[Tmin,Tmax],区间范围内的样本总数Np=N-N0．超过区间范围的样本一般较少,可选取随机生成的比较靠近区间端点的数据样本．将待模拟样本区间等间隔分为M个子区间,则每个子区间的温度增量δT为

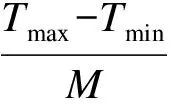
(4)

由此可知,第k个子区间的范围为 [(k-1)·δT,kδT],其中k=1,2,3,…,M．设第k个子区间的温度样本数量为Nk,则

(5)

(6)

根据各子区间的样本数量Nk,将ΔN按比例分配．设第k个子区间分配的多余样本数量为ΔNk,则第k个子区间最终的样本数量Npk为

Npk=Nk+ΔNk

(7)

由此便可将待模拟的概率密度分为M个子区间．当M足够大时,可近似认为每个子区间内的概率密度函数取值相等,即在子区间内有f(T)=C,其中C为常数．按照第k个子区间的样本数量Npk,生成[0, 1]之间均匀分布的随机数rand(Npk,0,1),则第k个区间的样本序列为 [(k-1)δT+T1+δT×rand(Npk,0,1)]．对所有子区间进行遍历,即可生成满足目标概率密度函数的序列．

图4 模拟温度样本的概率密度

图5 模拟温度样本的时程曲线

根据实测资料及当地气象记录,可以确定每年4个季节的日最高温度和日最低温度的范围,进而可以按照随机的原则从生成的样本中选取数据作为日最高温度和日最低温度．润扬大桥悬索桥实测的典型温度变化曲线以及国外研究结果[13]均表明,桥梁结构一天内的温度变化非常接近正弦曲线,故将每天的最高温度和最低温度作为正弦曲线的最大值和最小值,生成日温度的理想值．从生成的样本中选取与某时刻理想值最接近的样本,作为此时刻的模拟温度值,最终形成模拟温度时程．重排后的温度曲线见图6．由图可知,生成的样本时程曲线与实测结果的变化规律吻合良好,能够很好地反映扁平钢箱梁的日温度变化特性．

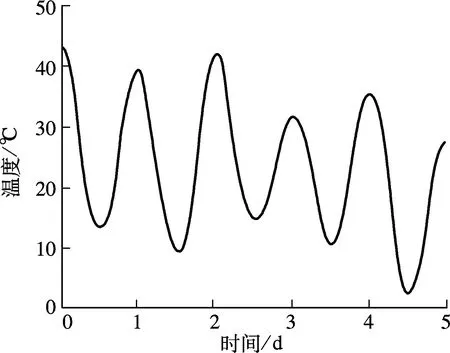
图6 重排后模拟温度样本的时程曲线

4.2 模拟结果

以润扬大桥悬索桥的实测温度结果为基础,生成为期5年的温度场数据．考虑到温差对扁平钢箱梁温度应力计算的重要性,要求模拟温度场的温差严格符合实测温差．因此,首先采用4.1节的方法生成参考点S2的随机温度样本序列以及各测点与参考点之间温差的随机样本序列,并从S2的样本序列中选取日最高温度和日最低温度．考虑到温差的随机性,根据模拟时间跨度的天数,从模拟温差样本序列中随机选取日最高温度的温差和日最低温度的温差．根据温差的定义,即可得出润扬大桥扁平钢箱梁横截面其他测点的日最高温度和日最低温度．对于其他测点的中间样本,同样可采用温差的定义获得．然后进行样本重排,即可获得润扬大桥扁平钢箱梁横截面温度场．测点S2和S7的模拟温度时程曲线见图7．由图可知,模拟温度时程曲线具有明显的四季变化特征,能很好地反映扁平钢箱梁横截面的年温度变化过程．

4.3 结果验证

对模拟样本进行概率密度函数估计,并与实测数据的概率密度函数进行比较,两者的最大误差见表3．此处,最大误差定义为概率密度最大差值除以最大差值对应点的实测数据概率密度．由表可知,概率密度值误差值最大不超过5%,说明采用本文方法能够准确模拟桥梁结构钢箱梁的温度场．

图7 测点S2和S7的模拟温度时程曲线

表3 模拟温度样本的概率密度最大误差

5 结论

1) 扁平钢箱梁横截面实测温度可采用2个正态分布的加权和组成的概率密度函数进行估计,估计结果能准确反映实测温度的统计特性．顶板上处于对称位置处的2个测点之间以及底板测点之间具有相同的温度分布特性．

2) 扁平钢箱梁横截面实测温差服从1个Weibull分布和1个正态分布的加权和.不同测点之间温差存在较大的差异,估计的概率密度函数与实测结果符合较好．

3) 数值逆变换抽样方法是对逆变换抽样方法的改进,使其可以应用于复杂概率密度函数下的样本生成,且可以根据需要生成不同长度的样本．重排后的基于数值逆变换抽样方法模拟的温度样本时程曲线符合桥梁结构的日温度变化规律．

4) 采用数值逆变换抽样方法和样本重排模拟的扁平钢箱梁横截面温度场时程具有明显的四季交替特征,其时程曲线和统计特性均与实测结果具有良好的一致性,证明了本文方法的有效性．模拟生成的温度场可为润扬大桥悬索桥全寿命评估提供数据支持．

)

[1] Xia Y, Chen B, Zhou X Q, et al. Field monitoring and numerical analysis of Tsing Ma suspension bridge temperature behavior[J].StructuralControlandHealthMonitoring, 2013,20(4): 560-575.

[2] Im C K, Chang S P. Estimating extreme thermal loads in composite bridge using long-term measured data[J].InternationalJournalofSteelStructures, 2004,4(1): 25-31.

[3] 雷笑, 叶见曙, 王毅. 日照作用下混凝土箱梁的温差代表值[J]. 东南大学学报:自然科学版, 2008, 38(6): 1105-1109.

Lei Xiao, Ye Jianshu, Wang Yi. Representative value of solar thermal difference effect on PC box-girder[J].JournalofSoutheastUniversity:NaturalScienceEdition, 2008,38(6): 1105-1109. (in Chinese)

[4] 王蕾, 赵雪峰, 欧进萍. 东营黄河刚构-连续梁桥长期监测的温度分布规律分析[J]. 防灾减灾工程学报, 2010, 30(S1): 206-211.

Wang Lei, Zhao Xuefeng, Ou Jinping. Research on temperature characteristics of the Dongying Yellow River bridge based on long-term monitoring[J].JournalofDisasterPreventionandMitigationEngineering, 2010,30(S1): 206-211. (in Chinese)

[5] Xu Y L, Chen B, Ng C L, et al. Monitoring temperature effect on a long suspension bridge[J].StructuralControlandHealthMonitoring, 2010,17(6): 632-653.

[6] Kullaa J. Distinguishing between sensor fault, structural damage, and environmental or operational effects in structural health monitoring[J].MechanicalSystemsandSignalProcessing, 2011,25(8): 2976-2989.

[7] Mirambell E, Aguado A. Temperature and stress distributions in concrete box girder bridges[J].JournalofStructuralEngineering,ASCE, 1990,116(9): 2388-2409.

[8] 葛耀君, 翟东, 张国泉. 混凝土斜拉桥温度场的试验研究[J]. 中国公路学报, 1996, 9(2): 76-83.

Ge Yaojun, Zhai Dong, Zhang Guoquan. Temperature gradient test and research of rc cable-stayed bridges[J].ChinaJournalofHighwayandTransport, 1996,9(2): 76-83. (in Chinese)

[9] Tong M, Tham L G, Au F T K, et al. Numerical modelling for temperature distribution in steel bridges[J].ComputersandStructures, 2001,79(6): 583-593.

[10] 孙国晨, 关荣财, 姜英民，等. 钢-混凝土叠合梁横截面日照温度分布研究[J]. 工程力学, 2006, 23(11): 122-128.

Sun Guochen, Guan Rongcai, Jiang Yingmin, et al. Sunshine-induced temperature distribution on cross section of steel-concrete composite beams[J].EngineeringMechanics, 2006,23(11): 122-128. (in Chinese)

[11] Ni Y Q, Ye X W, Ko J M. Monitoring-based fatigue reliability assessment of steel bridges: analytical model and application[J].JournalofStructuralEngineering,ASCE, 2010,136(12): 1563-1573.

[12] Castillo E, Hadi A S, Balakrishnan N, et al.Extremevalueandrelatedmodelswithapplicationsinengineeringandscience[M]. Hoboken,NJ, USA: Wiley, 2005.

[13] Backer H D, Outtier A, Bogaert P V. Numerical and experimental assessment of thermal stresses in steel box girders[C]//ProceedingsoftheEleventhNordicSteelConstructionConference. MalmÖ, Sweden, 2009:65-72.