方向导数的解法分析与探索＊

章丽娜，唐荣荣

（湖州师范学院 理学院，浙江 湖州313000）

方向导数是研究多元函数性态的有效手段［1～3］，在自然科学的许多领域中都有广泛的应用［4～6］.许多实际问题的探讨归结到数学上，往往不但要考虑函数沿各个轴向的变化率即偏导数，还必须研究函数沿任意指定方向的变化率，即对指定方向的方向导数.

在方向导数这部分内容的教学中我们发现，当指定方向以某一曲线的切线正方向、内法线方向以及外法线方向等形式给出时，学生屡屡因对公式中的方向向量表达式把握不准而造成计算失误，且求解方向导数的方法比较单一.因此探讨相关概念内涵、解决问题的不同方法和途径，提升学生的思维能力，提高解决问题的灵活性，是这部分内容课堂教学中的重点.

1 问题的提出

对于方向导数，高等数学课本上的相关例题通常是直接利用方向导数的公式进行计算［7］.一般来说，当方向向量的坐标已知时，利用公式直接计算的确方便.但在探讨具体问题时，方向往往通过某些条件来给定，相应的方向向量的坐标需要根据条件来确定.这种情况下，直接利用公式进行计算方向导数较容易出错.如文献［7］中有以下典型题目：

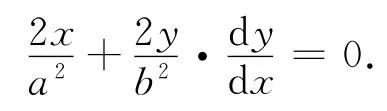
于是

法线斜率为：

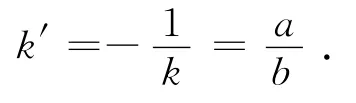
故内法线方向l＝（－b，－a）.于是由公式得到所求的方向导数为：

表面看来，此解答好像无误，但仔细推敲，却发现存在问题.事实上，在求方向导数的计算公式中，内法线方向的坐标表示是一个关键.从椭圆曲线的图像容易知道，当点P位于第一、三象限时，解法中的结论正确，此时l＝（－b，－a）；而当点P位于第二、四象限时，解法中的结论错误，此时内法线方向l应为（b，a），因此所得的方向导数错误.那么问题究竟出在哪里？思考上述解答过程，不难发现以上求得的k仅仅是切线的斜率，因此相应的k′仅是法线的斜率.斜率和方向向量确有关系，但当时，内法线的方向向量究竟是取（－b，－a）还是（b，a）？在上述解法中从直接将内法线的方向向量取为（－b，－a），显然缺少理论依据.事实上这需要根据点P所在象限进一步探讨，因此以上从法线斜率切入，直接应用方向导数公式进行计算容易出错.

2 问题的探讨

怎样避免上述错误的发生？从理论上说是要解决在点P处内法线方向向量的确定问题.

2.1 利用向量值函数的导向量求方向导数

向量值函数及其导向量是学生已经学过的内容，我们可利用这部分内容来解决以上问题.

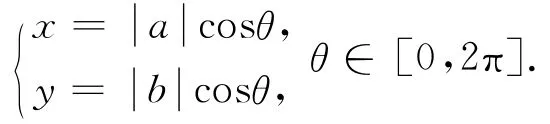
假设曲线Γ上的点

对应的参数，θ＝θ0，则向量函数（θ）在点P处的切向量为＝（－.

注意到如下事实：曲线方程在向量形式下，其切向量总是指向参数增大的方向，且例中曲线Γ的内法线l的方向向量为切向量逆时针旋转角（见图1）.由向量旋转公式，将向量绕点A逆时针旋转角θ，得到的向量

图1 内法线的方向向量与切向量的关系Fig. 1 The relationship between the direction vector of interior normal and the tangent vector.

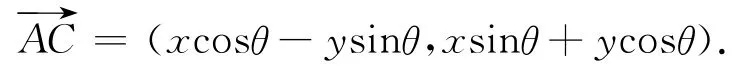
因此切向量逆时针旋转角得到的内法向量为.又由条件知：

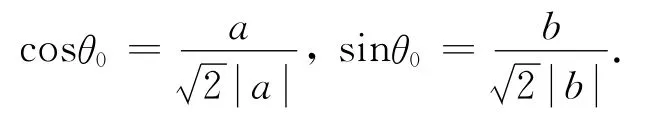
本方法利用向量值函数具有导向量总是指向参数增大方向的几何特性，先求得曲线在点P处的切向量，再借助向量旋转公式求得曲线在点P处的内法线的方向向量.无论是切向量，还是内法线方向向量，其方向都是唯一的.减少了利用切线斜率求解时还须借助曲线图形，根据点P所在的象限分类探讨切线的方向向量以及内法线的方向向量这一过程，避免了因中间讨论过程繁琐而发生错误.特别使我们感兴趣的是，以上给出的利用向量值函数的导向量来求方向导数的方法适用范围更宽泛，因无需借助曲线图形，所以对于更一般的曲线在定点处可顺利求得指定方向的方向导数.

2.2 利用函数在一点处的梯度求方向导数

回顾上述（1），我们利用向量值函数导向量的几何特性给出了求定点处方向导数的方法，这种解法思路简单，涉及的知识较浅显，学生易于接受.但是采用的仍然是迂回战术，即先对向量函数求导向量，再利用向量旋转公式求内法线的方向向量.仔细分析，这种方法虽然避免了按点P点所在的象限分类讨论，但在求解的过程中仍有一个问题需要判定，即需要判定曲线随着参数增加的方向，因为该方向确定了导向量的方向，从而确定了求内法线方向时到底是由切向量逆时针旋转角还是顺时针旋转角.为此我们给出如下一种求得方向导数更直接的方法.

由梯度定义知，如果函数f（x，y）在点P（x，y）可微＝（cosα，cosβ）是与方向l同向的单位向量，则其方向导数为：

这里▽f（x，y）＝（fx（x，y），fy（x，y））是函数z＝f（x，y）在点P（x，y）处的梯度，θ是梯度向量与方向l的夹角.由此不难得出如下结论：

函数f（x，y）在一点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值.

考虑曲面z＝f（x，y）上的曲线在xOy面上的投影曲线f（x，y）＝c，其中c为常数，于是得到了一族等值线.

易知，点P（x，y）处的法线的斜率为：

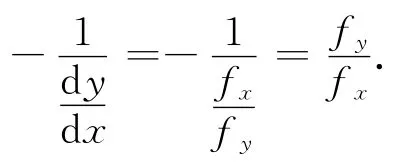
由梯度的定义可知，当函数f（x，y）在点P处可微时，函数f（x，y）在点P的梯度的方向即过点P的等值线f（x，y）＝c在这点处的法线的方向向量，且从数值较低的等值线指向数值较高的等值线，而梯度的模就等于函数在这个方向的方向导数（见图2）.因此，可利用函数在一点处的梯度方便地求得方向导数.

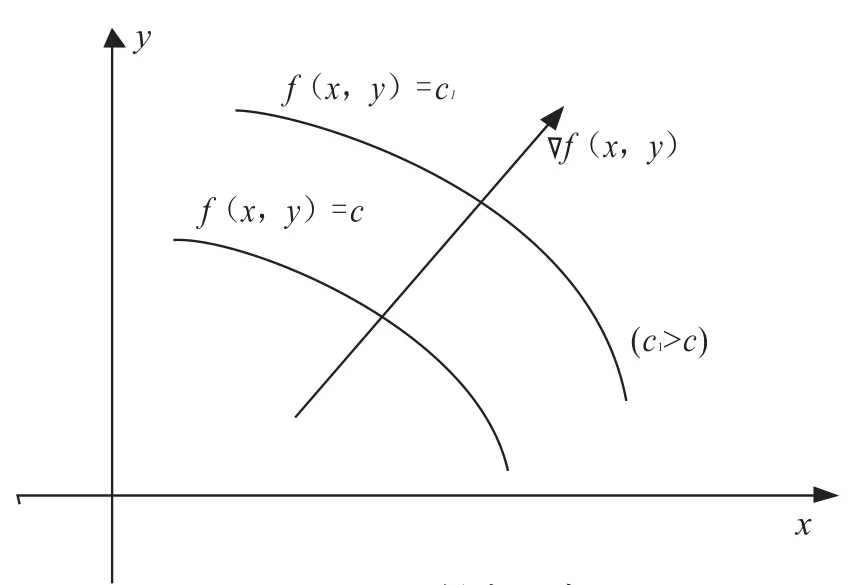
图2 梯度示意图Fig. 2 The gradient diagram

本方法利用梯度的几何解释以及梯度和方向导数之间的联系简捷地求得了曲线在定点处的方向导数.

综上所述，笔者给出了文献［2］之外的两种求方向导数的方法.从以上探讨，我们看到高等数学课程中概念和计算方法通常不是孤立的.在适当的前提下，从不同的切入点与应用知识点之间的联系往往能获得解决问题的有效途径，能巩固和加深对知识的掌握，从而能灵活地解决问题.因此，在教学中深化概念内涵、剖析知识点间的联系、提炼方法是值得我们不断探索的课堂教学环节.

［1］沈永红，高忠社.多元函数微分学中几个基本概念之间的关系［J］.高等数学研究，2009，12（2）：33－36.

［2］陈朝辉.利用方向导数探讨多元函数的单调性与极值［J］.宜宾学院学报，2010，10（6）：23－25.

［3］邵琛，陈东彦.非光滑函数的凸性［J］.数学的实践与认识，2002，32（1）：75－78.

［4］聂鹏飞，李月，曾谦，等.方向导数迹变换面波压制［J］.地球物理学报，2012，55（6）：2035－2043.

［5］余国林.方向导数和广义锥——预不变凸集值优化问题［J］.数学学报，2011（5）：875－880.

［6］陈武，靳海兵，吴政，等.基于方向导数的多光谱图像快速融合新算法［J］.计算机仿真，2009，10（26）：257－260.

［7］同济大学数学系.高等数学（下册）［M］.北京：高等教育出版社，2007：101－108.

［8］同济大学数学系.高等数学习题全解指南（下册）［M］.北京：高等教育出版社，2007：65－66.