Cn＋1filiform 李代数的左对称代数结构＊

吴明忠

（西华师范大学 数学与信息学院，四川 南充637009）

0 引 言

左对称代数是近年来从微分几何——李群的研究中提出的代数体系，而且当其基域变为任意域时，它与李群也有密切的联系［1］.

令A是域K上的向量空间，如果在A上有一个双线性的乘法

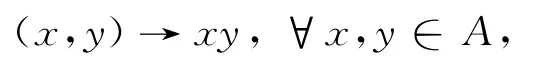
满足条件

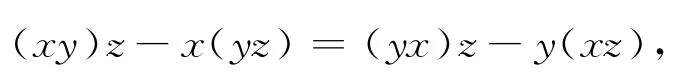
那么A就称为一个左对称代数.

如果在左对称代数A上定义一个括积如下：

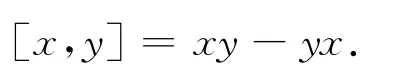
那么A构成一个李代数.称这个李代数与左对称代数A相邻，仍然用A来表示这个李代数，同时称这个李代数具有该左对称代数结构.

一个自然的问题是，哪些李代数具有左对称代数结构？我们知道，如果李代数A具有左对称代数结构，那么有［A，A］≠A.特别的，半单李代数不存在左对称代数结构［2］.

从上世纪60年代M.Vergne引入了filiform 李代数以来［3］，filiform 李代数，特别是Ln、Qn以及他们的形变一直是李理论研究的热点之一，其结果对rigid李代数的分类起到了重要作用［4］.而Cn＋1filiform李代数是一类重要的秩为1 的filiform 李代数.

本文通过求得Cn＋1filiform 李代数的极大环面证明了Cn＋1filiform 李代数具有左对称代数结构.

1 预备知识

定理1［5］如果N是一个幂零李代数，那么下面的说法等价：

（1）｛x1，x2，…，xn｝是一个极小生成元系（msg）；

（2）｛x1＋C1N，…，x2＋C1N，xn＋C1N｝是向量空间的N／C1N一组基.

在上述情况，我们称N是一个n型幂零李代数.

定义1［6］李代数N的一个环面是由可对角化线性变换组成的DerN的一个可交换的子代数.一个环面被称为是极大的，如果它不真正包含在任意一个环面子代数中.

引理1［7］如果H1和H2都是幂零李代数N的极大环面，那么存在N的自同构θ∈AutN，使得H2＝θH1θ－1.

由于一个幂零李代数N的所有极大环面都是相互共轭的，那么极大环面的维数就是幂零李代数N的一个不变量，我们称为N的秩，记为rank（N）.

引理2［8］令N是一个型幂零李代数，那么rank（N）≤n.当rank（N）＝n时，称N是极大秩幂零李代数.

定义2［3］令N是一个n维李代数，N被称为filiform李代数，如果满足条件dimCiN＝n－i－1，1≤i≤n－1.

定理2［9］任意一个秩为1的（n＋1）维filiform 李代数同构于以下的李代数之一，

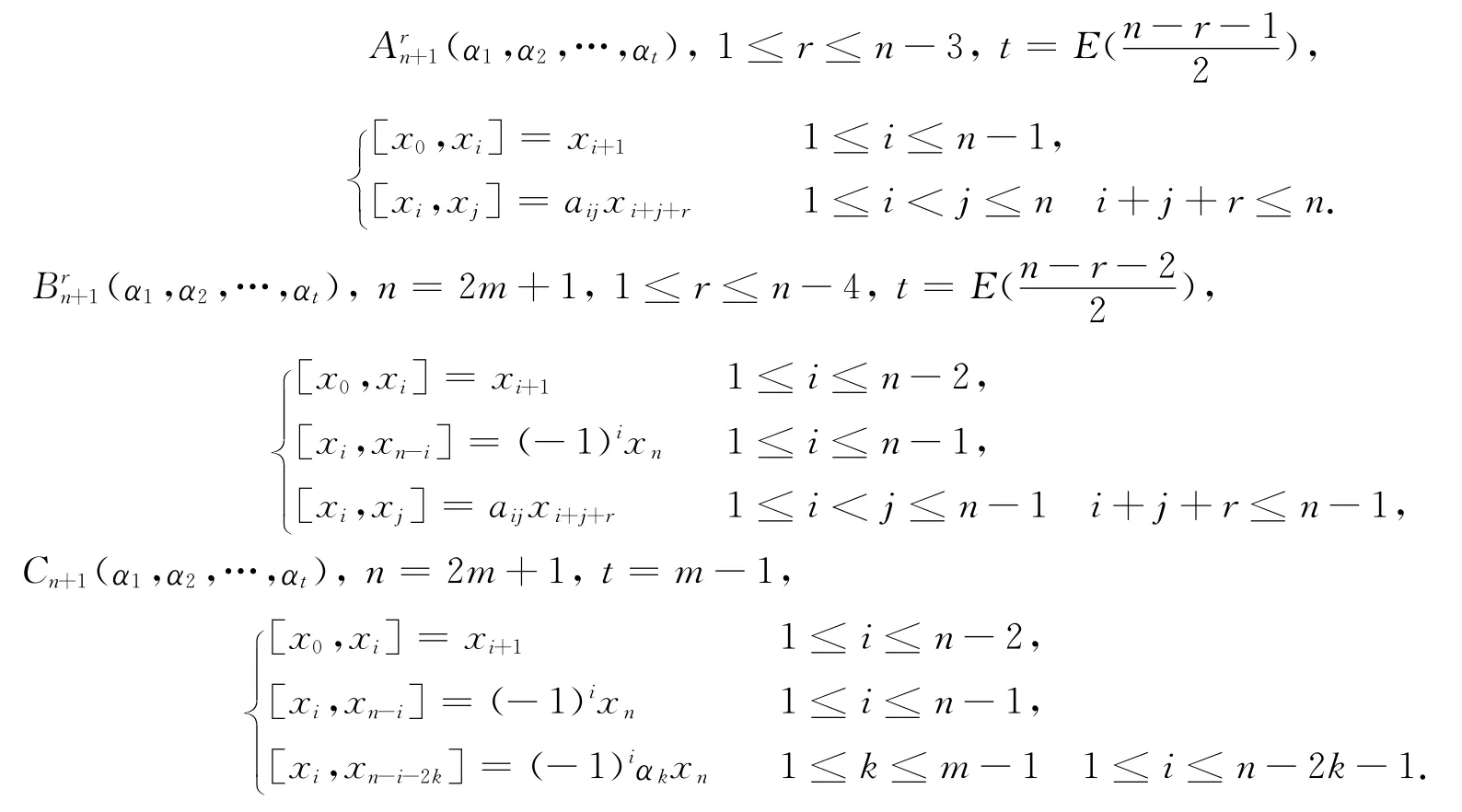
2 主要结果及证明

在本节中，我们求得了Cn＋1filiform 李代数的一个半单导子，从而求得他的一个极大环面，证明Cn＋1filiform 李代数具有左对称代数结构.下面的引理是显然的.

引理3 令σ是李代数N的一个线性变换，那么σ∈DerN的充分必要条件是在N的一组基｛X1，X2，…，Xn｝上σ满足条件：对于任意的1≤i，j≤n，都有：

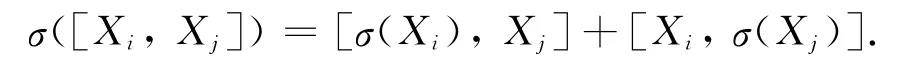
运用这个结论可以得到：

引理4Cn＋1有一个由φ∈Der（Cn＋1）生成的极大环面，其中φ是：

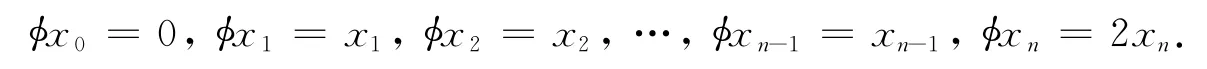
证明 假设D是Cn＋1的一个可对角化的线性变换

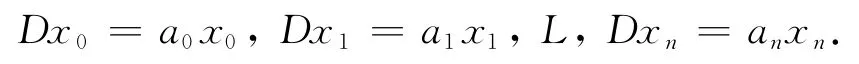
由引理3容易知道D是Cn＋1的一个导子当且仅当下面的式子成立：

解这个线性方程组我们得到：

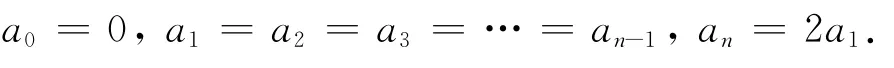
所以有：

特别的，Cn＋1的一个线性变换φ

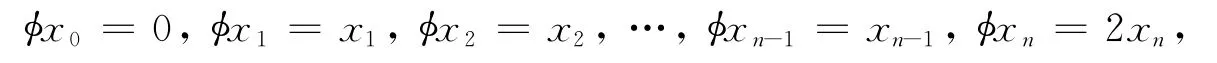
是Cn＋1的一个半单导子，因此φ可以生成Cn＋1的一个环面子代数.但是由定理2知道，Cn＋1是一个秩为1的filiform 李代数，所以φ生成的这个环面子代数还是一个极大环面子代数，所以φ生成Cn＋1的一个极大环面.

定理3Cn＋1filiform 李代数具有左对称代数结构.

证明 容易知道一个重要的事实，如果一个李代数具有非奇异的导子，那么这个李代数就具有左对称代数结构.

实际上，如果D是一个非奇异导子，那么令xy＝D－1［x，Dy］，则这个乘积使得该李代数构成左对称代数，因为

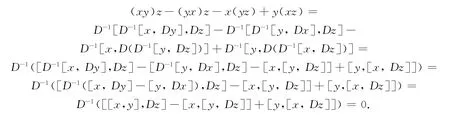
而由引理4得到了Cn＋1的一个导子：

这个导子虽然是奇异的，但从上面的证明可以看出，一个李代数的导子如果在这个李代数的导代数上是非奇异的，那么我们上面的证明过程也是成立的.明显的，李代数的导代数是任意一个导子的不变子空间，而导子：

在［Cn＋1，Cn＋1］上是非奇异的.所以Cn＋1filiform 李代数具有左对称代数结构.

［1］Burde D.Affine structure on nilmanifolds［J］.Intelnat J Math，1996（7）：599－616.

［2］Helmstettret J.Radical dune algebre symetrique a gauche［J］.Ann Inst Fourtier，1979（29）：17－35.

［3］Vergne M.Cohomologie des algebres de Lie nilpotentes，Application a l＇etude de la variete des algebres de Lie nilpotentes［J］.Bull Soc Math，France，1970（98）：81－116.

［4］Goze M，Khakimdjanov Y.Nilpotent Lie Algebras［M］.Mathematics and Its Applications，361，Dordrecht，Kluwer Academic Publishers Group，1996.

［5］Bourbaki N.Groupes et algebres de Lie［M］.Ch I Hermann，Paris，1960.

［6］Santharounane L J.Kac－Moody Lie algebra and the classification of nilpotent Lie algebras of maximal rank［J］.Canad J Math，1982，34：1 215－1 239.

［7］Mostow G D.Fully reducible subgroups of algebaic groups［J］.Amer J Math，1956（78）：200－221.

［8］Meng D J，Zhu L S.Solvable complete Lie algebras I［J］.Comm Alg，1996（24）：4 187－4 197.

［9］Goze M，Khakimdjanov Y.Sur les algebres de Lie nilpotentes admettant un tore de derivations［J］.Manu Math，1994（84）：115－124.