压裂液单相滤失模型适用条件研究
2013-12-23李勇明张秦汶李亚洲
罗 攀,李勇明,张秦汶,李亚洲,王 楠
(“油气藏地质与开发工程”国家重点实验室·西南石油大学,四川成都610500)
近年来建立的一些滤失模型考虑到了越来越复杂的油藏条件,但求解的难度也变大。单相滤失假设能够极大地简化复杂情况下的滤失问题,便于计算分析。任岚[1]等将滤失视为二维流动,考虑了压裂液的非牛顿性,建立了高渗透地层的二维滤失模型;李勇明[2]等考虑到油藏介质的不均匀性,建立了一系列的双重介质、多重介质的滤失模型,得到了经典滤失理论不适宜于多重介质储层滤失计算的结论,对裂缝性地层、裂缝-溶洞性地层的滤失计算有重要意义;黄志文[3]等考虑了温度对压裂液流变性的影响,提出了考虑温度场影响的滤失计算方法。上述模型都建立在压裂液单相滤失假设的基础上,单相假设可以简化问题,但使用假设前应先解决假设是否合理、以及引起多大的误差这两个问题。本文试图在考虑两相流体性质差异的滤失模型的基础上比较两相滤失与单相滤失的差异,以明确单相滤失假设的合理条件,确定单相滤失假设的误差范围。
1 两相滤失数学模型[4-12]
假设压裂液活塞式驱替油藏流体(图1),侵入区压力分布函数为p1(x,t),0<x<xc(t);油藏区压力分布函数为p2(x,t),xc(t)<x<+∞;流体界面处的压力为pc;界面处的压力满足连续性方程:
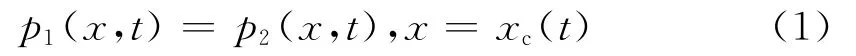
界面处的滤失速度相等:

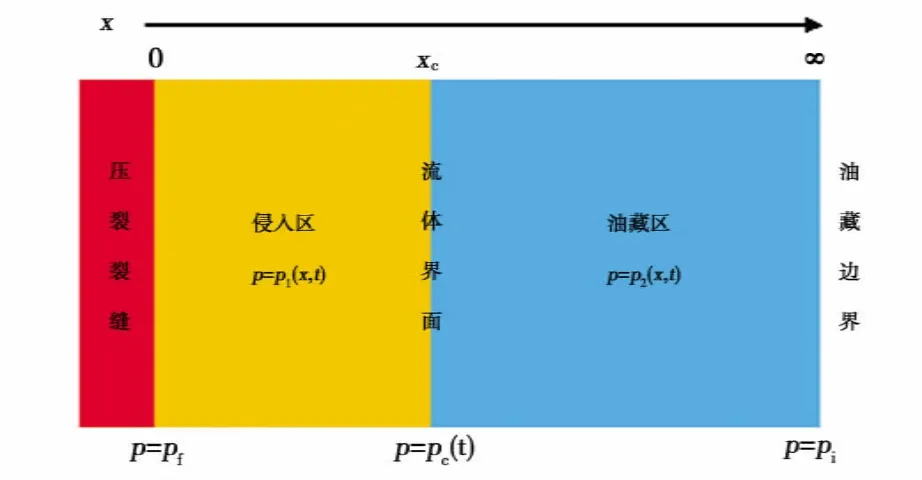
图1 压裂液活塞式驱替油藏流体示意图
设储层渗透率为K,孔隙度为φ,岩石孔隙压缩系数为cf,油藏流体粘度为μ2,压缩系数为cc,压裂液粘度为μ1,压缩系数为cv,油藏初始压力为pi,则两相滤失压力计算方程:
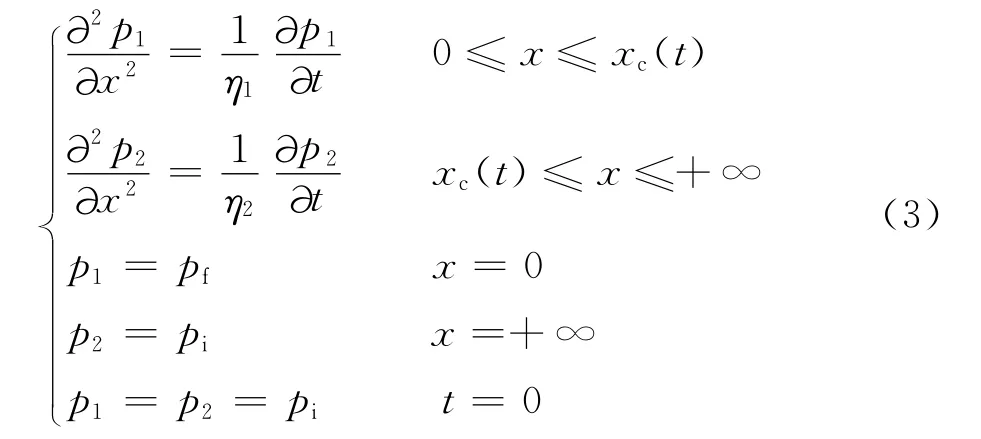
其中,η1 为侵入区导压系数,η2 为油藏区导压系数,c1为侵入区综合压缩系数,c2为油藏区综合压缩系数,由下式计算:
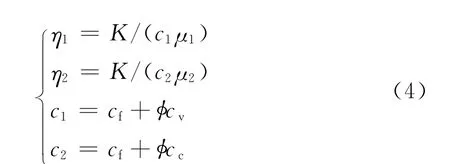
2 两相滤失模型的求解
令

作玻尔兹曼变换
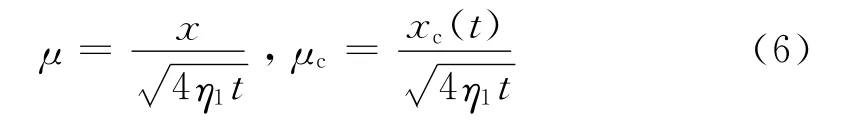
可将(3)式化常微分方程组的边值问题:

设满足方程边界条件与初始条件的解为
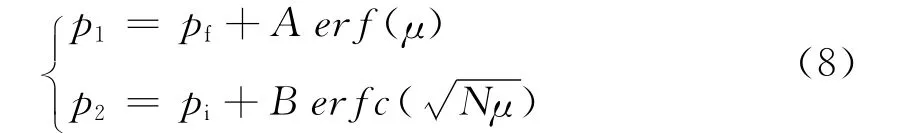
式中,erf(x)为高斯误差函数,erfc(x)=1-erf(x)。
单位面积的裂缝壁面与流体界面之间包含的流体体积为:

时间t内单位面积裂缝壁面的流体滤失量为:
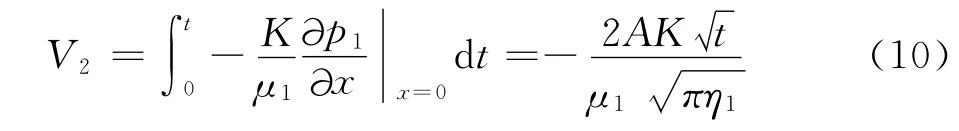
若令时间t等于流体界面从裂缝壁面运动至xc处所花费的时间,那么V1与V2应该相等,即

整理,得

由界面处流速条件(2)可得

界面处压力条件(1)可表示为
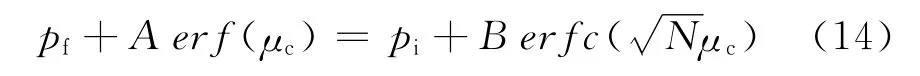
将(12)、(13)带入(14)式,并整理可得

用迭代法即可解出uc,并将其带入(8))式便可得求出A、B,从而得到压力分布函数p1、p2。裂缝壁面上的滤失速度则可按(16)式计算。

裂缝壁面上的滤失量则为:

3 单相滤失误差计算
为了比较两相滤失与单相滤失的差异,可推导只考虑压裂液单相存在的滤失计算式(18)。

若将单相流动假设引起的相对误差控制在δ以内,则(16)、(18)式应满足

整理,得

将(12)、(15)带入(20)式,并略去一些影响较小的项,有:
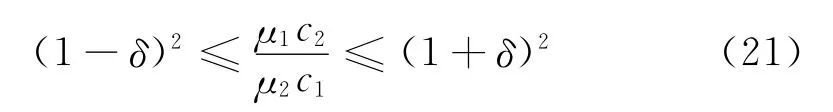
结合(4)式,得:

当压裂液与油藏流体的粘度与压缩系数满足(22)式时,将两相滤失简化为单相滤失的相对误差上限为δ。
4 应用分析
根据以上模型编制了VB 程序进行计算分析。基本数据如表1所示。
图2为计算得到的两相滤失速度与单相滤失速度曲线对比,两相滤失速度为单相滤失速度的数倍,主要原因为油藏流体小于压裂液粘度,两相滤失阻力远小于单相滤失的阻力。
图3为流体粘度差异对滤失速度之比的影响,图4为流体压缩系数差异对滤失速度差异的影响。油藏流体与压裂液的性质差异越小,两相与单相滤失速度越接近。若两种流体粘度与压缩系数均相等,这实际等同于单相滤失的情形,两相滤失速度与单相滤失速度是完全一致的。

表1 程序输入数据
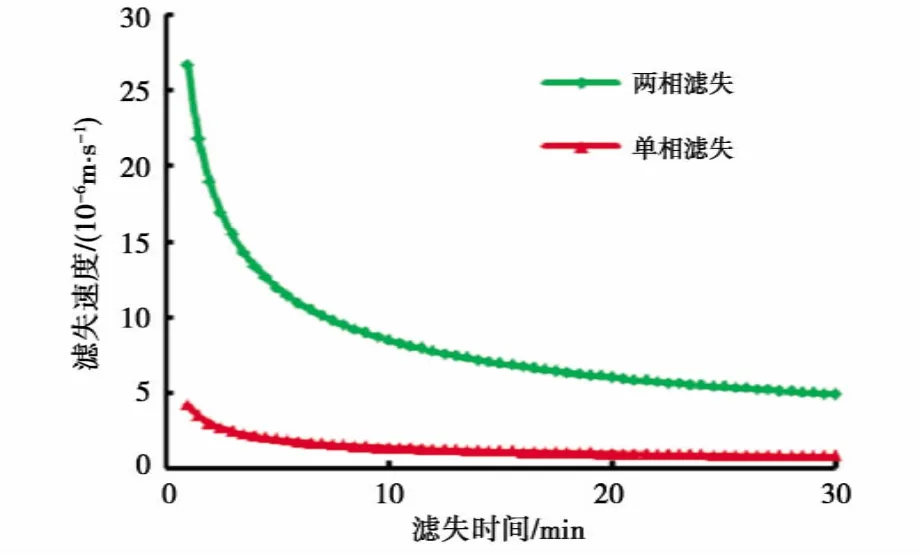
图2 两相滤失与单相滤失的差异

图3 粘度差异对两相滤失速度的影响
图5为满足(22)式的两相滤失曲线(从上至下δ分别为0.1,0,0.17),与单相滤失曲线的对比。单相滤失假设引起的误差在20%之内,说明当流体性质差异满足一定条件的时候,两相滤失是完全可以假设为单相滤失的。
图6为流体界面附近的压力分布,两相流体的压力分布曲线在界面处有明显的转折,符合两种性质差异较大的流体在界面处有相同的压力、相同的流速的实际情况。图7为远场区域的压力分布,区域的压力分布为油藏流体的性质所控制,压裂液对该区域的压力分布的影响很小。

图4 压缩系数差异对滤失速度的影响

图5 可以将两相滤失当作单相滤失的情形(cv=0.0007 MPa-1,μ1=100 mPa·s)

图6 流体界面附近的压降曲线
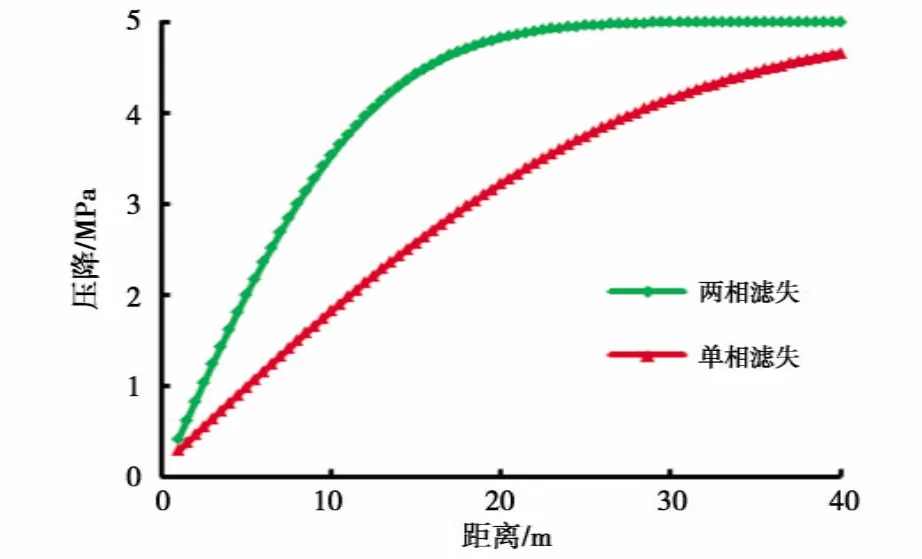
图7 远场区域的压降曲线
5 结论
(1)压裂液滤失是压裂液驱替油藏流体的两相或多相渗流过程。由于油藏流体与压裂液的粘度、压缩系数存在差异,滤失计算时不能一概将滤失过程假设为压裂液的单相渗流,否则可能会引起较大误差。
(2)当油藏流体与压裂液性质满足一定条件时,两相滤失可以简化为压裂液的单相滤失。
(3)本文建立的两相滤失的计算模型易于求解,具有一定推广应用价值。
(4)在需要大量重复进行滤失计算的压裂模拟设计中,可先估算单相滤失的误差范围,若误差不大,可使用单相渗流假设的模型,以便于考虑其他复杂条件;若误差较大,建议使用两相滤失的模型。
[1] 任岚,胡永全,赵金洲,等.高渗透地层压裂液滤失模型研究[J].天然气工业,2006,26(11):116-118.
[2] 李勇明,郭建春,赵金洲,等.裂缝性储层压裂液滤失计算模型研究[J].天然气工业,2005,25(3):99-102.
[3] 黄志文,李治平,王树平,等.压裂施工闭合过程压裂液滤失分析[J].油气井测试,2007,16(3):8-10.
[4] 古发刚,任书泉.多种因素下的滤失速度计算模型[J].西南石油学院学报,1991,13(2):65-711.
[5] 付永强,郭建春,赵金洲,等.一种多参数的压裂液在双重介质中滤失模型的推导与计算[J].天然气工业,2003,23(3):88-91.
[6] 孔祥言.高等渗流力学[M].合肥:中国科学技术大学出版社,1999.
[7] 程林松.高等渗流力学[M].北京:石油工业出版社,2011.
[8] 纪国法,姜雨省,陈亮,等.浅析滤失性研究现状[J].重庆科技学院学报(自然科学版),2012,14(4):73-77.
[9] Ribeiro L H,Sharma M M.Multi-phase fluid-loss properties and return permeability of energized fracturing fluids[C].SPE139622,2011.
[10] Wang J Y,Holditch S A,Mcvay D A,et al.Modeling fracture fluid cleanup in tight gas wells[C].SPE 128067,2009.
[11] 李勇明,纪禄军,郭建春,等.压裂液滤失的二维数值模拟[J].西南石油学院学报,2000,22(2):43-47.
[12] 张保平.油藏增产措施(第3版)[M].北京:石油工业出版社,2002.
