优化STR 模型的实证研究

昌春艳，王 沁，田 锟，刘 娟

(1.西南交通大学 数学学院，四川 成都610031;2.四川建筑职业技术学院 计算机工程系，四川 德阳618000;3.西华师范大学 数学与信息学院，四川 南充637002)

经济增长意味着国民经济规模的扩大和数量的增长。发现经济增长源泉，并采取措施实现经济增长，是人们一直探索的目标，同时也是社会发展和政治稳定必须要面临的重大课题。经济增长的原因、其内在机制以及实现途径，是经济理论研究中的核心问题。GDP 是衡量一个国家经济发展的最佳指标。工资总额与GDP 的关系一定程度上反映了国家市场经济的成熟度，也是衡量社会分配公平与否的重要内容。目前，工资总额与GDP 关系的研究多基于线性回归和定性研究。张金玲［1］利用1981—2004 年的相关数据得出结论，工资总额与GDP 呈正相关关系。李姗姗利用1991—2006年的数据，通过OLS 回归，得到工资总额与GDP 的线性表达式［2］。在工资总额和GDP 关系的研究中，两者之间的函数关系是否会一成不变，是否始终保持一个线性关系是值得探讨的问题。STR 模型是非线性时间序列分析的前沿及热点内容，已成为非线性关系分析的典型工具之一。

1 STR 模型与两种参数估计方法

1.1 STR 模型

平滑转换自回归模型(smooth transition auto－regression model，STAR)是由GRANGER 等提出的［3］，目前已经形成了一套较为成熟的建模程序，包括模型的设定、估计和诊断测试，STAR 模型的提出为STR 模型奠定了理论基础。平滑转换回归模型是对STAR 模型的改进和发展，也是门限回归模型的一般化形式，其主要的特征是能刻画不同体制下金融变量、经济增长变量等指标之间的非对称、非线性的相依动态关系。

STR 模型的一般表达式如下［4］:

式中:yt为目标变量，表示具体的经济成果;xt为解释变量，其中包括目标变量yt直到k 阶的滞后变量和m 个其他解释变量，即有:xt=(1，x1t，…，xpt)′ =(1，yt－1，…，yt－k，z1t，…，zmt)′，且有p =k+m;φ=(φ0，φ1，…，φp)′和θ =(θ0，θ1，…，θp)′分别为线性和非线性部分的参数;εt为独立同分布的误差，一般假设其服从正态分布;转换函数G(st;γ，c)是一个取值范围为［0，1］的连续函数，既可以是单调递增的奇函数，如分布函数，也可以是对称的偶函数，如密度函数，描述指标在不同体制下平滑过渡;st为开关变量，即阈值，既可以是单个随机变量，如xt的一个元素，也可以是多个随机变量或者线性时间趋势的线性组合。

对于转换函数G(·)，常见的形式是logistic函数形式和指数函数形式，其中logistic 函数形式的表达式为:

式(1)和式(2)构成了logistic 平滑回归模型，即LSTR 模型。斜率γ 反映了由LSTR 模型描述的状态“0”过渡到状态“1”的速度大小及转换的平滑性。阈值参数用来确定状态转变的时刻。

指数函数形式的表达式为:

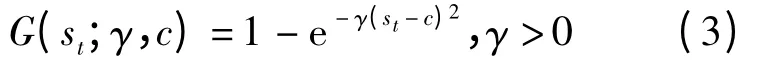
式(1)和式(3)构成了指数平滑回归模型，即ESTR 模型。该模型也是以c 点为转换变量的转折点，但与LSTR 模型又有所不同，ESTR 模型的转换函数图像是关于直线st=c 对称，也反映出转换变量对目标变量影响的一种对称性。当转换函数G(st;γ，c)→0 时，模型的非线性部分逐渐消失，退化为线性模型。

1.2 建立模型的步骤

使用STR 模型进行实证的步骤如下［5－7］:

(1)数据预处理。STR 模型针对平稳时间序列比较适合，因此，先检查数据的平稳性，进行差分、季节差分等将数据转化为平稳时间序列，然后进行格兰杰因果检验，确定因变量与自变量。

(2)确定自回归(AR)部分的滞后阶数。

(3)线性AR 模型与STR 模型的选择。以被解释变量与解释变量之间是线性AR 模型为原假设，STR 模型作为备择假设的模型，进行假设检验，从而完成模式识别。

(4)STR 模型的类型选择，即选择建立LSTR模型还是ESTR 模型。

(5)STR 模型参数的估计。

(6)STR 模型的分析与适应性检验。

1.3 参数估计原理

1.3.1 高斯－牛顿迭代法

高斯－牛顿迭代法的基本思想是使用泰勒展开式去近似地代替非线性回归模型，通过多次迭代，修正回归系数，得到最佳逼近非线性回归模型的回归系数，同时使原模型的残差平方和达到最小。

LSTR 模型在γ=0 的泰勒展开式为:

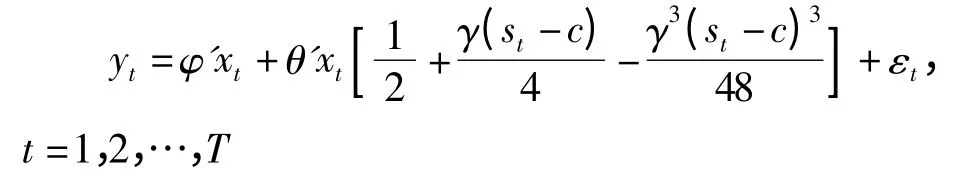
ESTR 模型在γ=0 的泰勒展开式为:

yt=φ′xt+θ′xt[ γ(st－c)2]+εt，t=1，2，…，T

在模型的参数估计中，高斯－牛顿迭代法依赖于参数初值的选择、泰勒展开阶数的选取，是一种将非线性转化为线性方程的处理手段。在残差服从正态分布的前提下，高斯－牛顿迭代法不一定能搜索到使实际值与估计值之差的平方和达到最小的参数估计值，且与参数的极大似然估计常常不一致，因此需要进一步优化参数的估计。

1.3.2 基于AIC 值优化参数估计

当STR 模型中参数γ 和c 为定值时，模型变为线性模型，在残差服从正态分布的前提下，参数的最小二乘估计就是极大似然估计［8］，即无偏的方差最小估计，这时参数得到了优化。

具体的做法是，先利用高斯－牛顿法估计参数γ 和c，再确定适当的步长，获得若干个γ 和c，将γ 和c 所有可能的取值形成组合，代入STR 模型中转化为线性模型，得到参数φ 和θ 的初步估计，结合AIC 和DW 值，进行进一步搜索，直到参数估计达到要求精度，从而优化参数估计［9］。

2 数据来源及预处理

2.1 数据来源

实证分析的时间段为1978—2007 年，共有30 个观测值，所采用的数据来自于《2011 年四川统计年鉴》，实证分析的软件为Matlab 和Eviews，分别用x、y 表示四川省的工资总额和GDP。

2.2 数据的预处理

不平稳的时间序列数据不能用来进行回归分析，否则将会出现“伪回归”现象。因此在建立模型之前要首先对数据进行平稳性检验。检查序列平稳性的标准方法是单位根检验，利用软件Eviews5.0［10］绘出x、y 的趋势图，发现它们并不平稳，对x、y 取对数，然后做两次差分，经过ADF 检验，可得到平稳时间序列ggx、ggy。

2.3 格兰杰因果检验

格兰杰因果检验对数据的平稳性是非常敏感的，尽管序列lx(序列x 的对数)和ly(序列y 的对数)的趋势图走势基本相同，但由于它们都不是平稳序列，因此只能采用序列ggx、ggy 进行格兰杰因果检验，检验结果如表1 所示。无论滞后阶数是1、2还是3，接受“ggx 不是ggy 的因”的概率p 值都小于接受“ggy 不是ggx 的因”的概率p 值，因此可以认为存在工资总额到经济增长的单向格兰杰因果关系，说明工资总额对四川省经济增长有很大的影响。

表1 格兰杰因果关系检验

3 模型建立与参数估计

3.1 模型的建立

3.1.1 滞后阶数的确定

由STR 模型，先要确定模型中包含的被解释变量的滞后阶数，在这里，除被解释变量滞后变量外，仅考虑工资总额这一因素对经济增长的影响，再按照SENSIER 和OSBORN 的做法，将模型的最高滞后阶数设定为8，从最高阶8 开始，根据AIC和SC 准则，将变量的t 检验值和DW 值逐一剔除，从中选择一个比较理想的滞后阶数［11］，其回归过程和滞后阶数选择的计算结果如表2 所示。

从表2 可以看出，在ggy 滞后一阶的情况下，AIC 与SC 之和达到了最小，DW 值也在2 左右，比较理想，各参数的p 值与处于同一行其他情况下的p 值相比也是最优的，因此通过该方法可以确定应该取被解释变量的滞后一阶作为解释变量的组成部分，但在上述分析中仅考虑了被解释变量的滞后情况，没有考虑作为解释变量ggx 的滞后情况。与上述分析过程类似，选取ggy 滞后三阶、ggx 滞后二阶组成9 种不同的组合，分别对ggy进行回归，回归结果如表3 所示。从表3 中(1，0)部分可知，ggx、ggy (－1)组合的各项指标是最优的，这与表2 的结果相同，因此可以确定模型最终的解释变量为ggx、ggy (－1)。

表2 ggy 对其前期取值和ggx 的回归结果

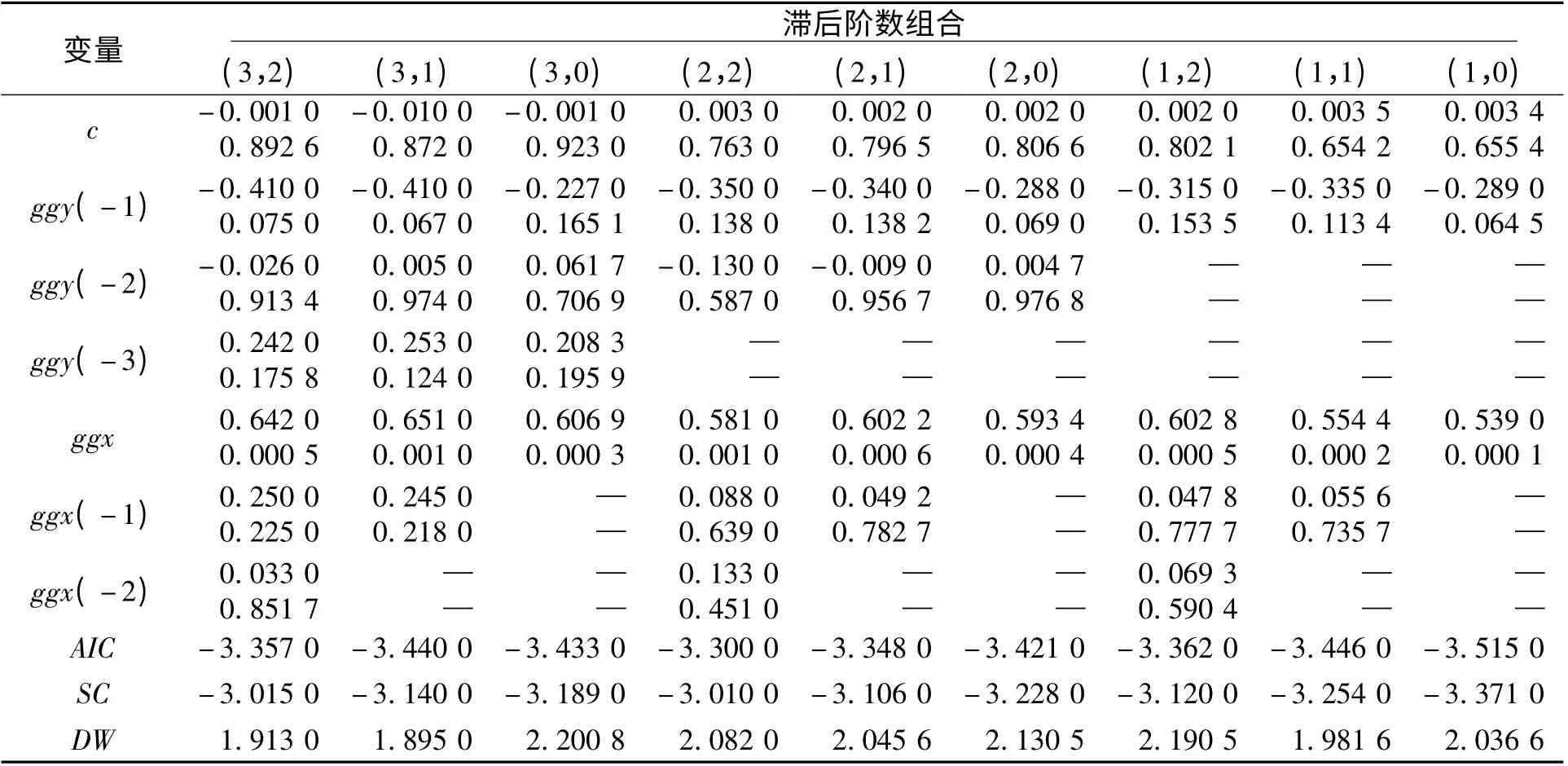
表3 各滞后变量组合对ggy 回归结果

3.1.2 线性检验及模型的选择

表4 线性假设检验和模型选择检验结果

3.2 参数估计

3.2.1 非线性最小二乘法估计参数

采用Eviews 软件进行计算得到的最小二乘法的参数估计结果如表5 所示。

表5 最小二乘法的参数估计结果

ggy=－0.015 8－0.538 9 ggx+0.326 1 ggy(－1)+［0.026 6 +0.126 9 ggx+0.382 9 ggy(－1)］G(yt－1;γ，c)

3.2.2 采用网格搜索法估计参数

将非线性STR 模型中的γ 和c 固定，模型变为线性的，通过非线性最小二乘法近似计算出γ 和c存在的可能区间，分别从最小值到最大值等间距对(γ，c)取值，γ 的取值范围为［1 340，1 350］，步长为0.01，c 的取值范围为［0，0.01］，步长为0.000 01。构造出1 000 ×1 000 对组合，针对每一对组合(γ，c)，采用Matlab 软件将(γ，c)代入目标函数中，依次观察模型的AIC、SC 值，然后筛选出AIC、SC 值较小，DW接近2 的参数组合作为最终结果。

根据AIC 准则和SC 准则，选择出最优模型，当γ=1 343.83，c=0.003 769 时，相应的AIC、SC都较小，DW 也更接近2，具体结果如表6 所示。

表6 网格搜索法的参数估计结果

ggy=－0.015 870－0.538 476 ggx+0.325 458 ggy(－1)+［0.026 755 +0.122 924 ggx +0.383 498 ggy(－1)］G(yt－1;γ，c)

4 结论

笔者利用非线性LSTR 模型研究四川省的GDP 与工资总额之间的动态关系，发现两者之间存在着明显的非线性和非对称关系。借助高斯－牛顿迭代法和搜索法对非线性STR 模型中的参数进行估计，在该过程中发现，高斯－牛顿迭代法是使用泰勒展开式去近似地代替非线性回归模型，优点是对所估计参数的检验较为简单，但计算结果有较大的误差，在实际运用中，往往存在对初始值的依赖性，以及可能得到局部最优的结果，却达不到全局最优，甚至可能存在迭代不收敛的情况。搜索法较好地克服了上述缺点，避免局部最优问题。将STR 模型中参数γ 和c 取为定值，模型退化为线性模型，这样得到在残差服从正态分布的前提下，参数的最小二乘估计就是极大似然估计、无偏的方差最小估计，优化了估计结果，得到全局最优参数估计。搜索算法也避免了高斯－牛顿算法中可能出现的迭代不收敛现象，且该算法是在高斯－牛顿迭代法近似计算出γ 和c 存在的可能区间的基础上去搜索γ 和c 的估计，使得计算量大大减小，得到的参数估计更为准确。

［1］ 张金玲. GDP 影响因素的计量分析［J］. 当代经理人，2006(11):205－206.

［2］ 李珊珊.中国工资调整指数研究［D］. 沈阳:辽宁大学图书馆，2009.

［3］ GRANGER C W J，TERASVIRTA T. Modelling non－linear economic relationships［M］. Oxford:Oxford University Press，1993:32－98.

［4］ 赵进文，范继涛. 经济增长与能源消费内在依从关系的实证研究［J］.经济研究，2007(8):31－42.

［5］ 李明贤，李学文.基于STR 模型的金融机构信贷资金投放与中国经济增长的实证研究［J］.系统工程，2009(1):57－63.

［6］ 谢赤，戴克维，刘潭秋.基于STAR 模型的人民币实际汇率行为的描述［J］.金融研究，2005(5):51－59.

［7］ 赵进文，闵捷. 央行货币政策操作效果非对称性实证研究［J］.经济研究，2005(2):26－34.

［8］ 彭方平.STR 模型及我国货币政策传导非线性研究［D］.武汉:华中科技大学图书馆，2007.

［9］ 王松贵，陈敏，陈丽萍.线性统计模型［M］.北京:高等教育出版社，2010:19－98.

［10］张晓峒.Eviews 使用指南与案例［M］.北京:机械工业出版社，2007:54－103.

［11］黄雁勇，王沁，李裕奇.ARMA 模型参数估计算法的改进［J］.统计与决策，2009(16):7－9.