交错三角格的链环分支数的几个结论
2013-12-22林跃峰
林跃峰
(漳州城市职业学院经济管理系,中国漳州 363000)
一个纽结是指三维欧氏空间的一条简单闭曲线.一个链环是指有限个互不相交的纽结缠绕在一起的图,每一个纽结称为链环的一个分支,一个链环包含的纽结的个数称为链环分支数.尽管链环图是三维欧氏空间图,我们总可以用链环投影图(即满足在每个二重投影点的邻近两短线上下互相穿越交叉的规则投影的投影图)来刻画链环.
平面图的平面嵌入称为平图,即无符号平图.一个符号平图指每条边都标有±号的平图.在纽结理论中,链环投影图与符号平图有着一一对应关系.这种对应被应用于构造链环图表[1].将链环投影图的交叉点置换成相交点,所得到的图对应于无符号平图的中间图.
文献[2]研究平图G 的左右回路数,即平图G 对应的中间图M(G)的直走闭迹回路数[3],也就是平图G通过中间图M(G)构造所对应的链环图L(G)的链环投影图D(G)的连通分支数.平图G 对应的链环分支数[4-5],记为μ(D(G)).研究平图的链环分支数,是研究通过平图的中间图构造对应的链环图的基本问题之一.文献[4,6]研究了一类链环,其分支数不小于对应的平图的基圈数.文献[7,8]分别研究了二维方格图Lm×n=Pm×Pn(如图1(a)所示)和三角格图Tm×n(如图1(b)所示)的链环分支数.文献[9]研究了扇图和轮图的链环分支数.关于图的结构和平图的链环分支数有关的工作,见文献[10~14].
由二维方格图Lm×n的每个小方格内分别增加一条对角边(如图1(c)所示),其左起奇数(偶数)列的小方格内增加的对角边以该小方格左下(上)角和右上(下)角的顶点为两端点,所得的m×n 交错三角格图记为ATm×n.本文研究交错三角格图ATm×(2m-2)(m≥2)和ATm×n(2≤m≤4)的链环分支数.

图1 (a)方格图Lm×n;(b)三角格图Tm×n;(c)交错三角格图ATm×nFig.1 (a)Quadrilateral lattices Lm×n;(b)Triangular lattices Tm×n;(c)Alternating triangular lattices ATm×n
1 几个已知的引理
下面是关于无符号平图的3 类Reidemeister 变换(以下简记为R-变换).无符号平图的R-变换对应于纽结理论中的链环投影图的3 类Reidemeister 变换.
Ⅰ变换:删除一个环或收缩一条割边.分别见图2 的Ⅰ(a)和Ⅰ(b);
Ⅱ变换:删除一对平行边或收缩一对序列边.分别见图2 的Ⅱ(a)和Ⅱ(b);
Ⅲ变换:YΔ-变换或ΔY-变换.见图2 的Ⅲ.

图2 平图的R-变换Fig.2 Plane graphical Reidemeister moves
令G1∪G2表示2 个图G1和G2的不交并.
引理1[14]平图G 在R-变换下:或删除环、或收缩割边、或删除一对平行边、或收缩一对序列边、或YΔ-变换或ΔY-变换,不改变其链环分支数.
引理2[7]设G 是平图,则μ(D(G))=k 当且仅当G 能通过有限次无符号平图的R-变换变换为空图Ok.
引理3[7]设G 和H 是2 个平图,x1,x2,…,xn和u1,u2,…,un分别是G 的外部面F 的n 个顶点和H 的某个面的n 个顶点.对于每个i(i=1,2,…,n),若dG(xi)≤1,设Ci是D(G)的围绕G 的顶点xi且将xi与G中其他顶点分离的分支;若dG(xi)>1,设Ci是D(G)的连续穿过面F 的边界上的顶点xi的2 条关联边且与G 的这2 个交叉点之间的连边在面F 内的分支.若μ(D(G))=n 且D(G)的分支C1,C2,…,Cn两两不同,则μ(D(G(x1,x2,…,xn)∪H(u1,u2,…,un)))=μ(D(H)).
2 交错三角格图ATm×(2m-2)(m≥2)的链环分支数
本节研究并证明交错三角格图ATm×(2m-2)(m≥2)的链环分支数.
将二维m×m 方格图Lm×m左起第一列小方格中的每一个小方格分别都增加一条以该小方格左下角和右上角的顶点为两端点的对角边,且对最后一行的除左起第一条边之外的每一条边分别都新增一个剖分点,这样得到的m×m 格图记为图Bm(图3(左边第1 个图)为图B5).
引理4设m 是正整数,且m≥2,则μ(D(Bm))=m.
证对正整数m 用归纳法证明.当m=2,3 时,因B2和B3可由平图的R-变换分别变换为O2和O3.由引理1 和引理2 知,μ(D(B2))=μ(D(O2))=2,μ(D(B3))=μ(D(O3))=3.故当m=2,3 时,结论成立.现在假设对于所有的m≤k(k≥3,k 为正整数),结论成立.则当m=k+1 时,因Bk+1可经平图的R-变换变换为Bk∪O1,见图3.由引理1、引理2 和归纳假设,知μ(D(Bk+1))=μ(D(Bk))+1=k+1.根据归纳法原理,引理4 成立.

图3 Bk+1变换为Bk∪O1Fig.3 Bk+1 is transformed to Bk∪O1
定理1设m 是正整数,且m≥2,则μ(D(ATm×(2m-2)))=m.
证当m=2 时,μ(D(AT2×2))=μ(D(B2))=2.当m >2 时,ATm×(2m-2)可经平图的R-变换变换为Bm,见图4.由引理1 和4 知,μ(D(ATm×(2m-2)))=μ(D(Bm))=m.

图4 当m >2 时,ATm×(2m-2)经平图的R-变换变换为BmFig.4 ATm×(2m-2)(m >2)is transformed to Bm by applying plane graphical Reidemeister moves
对于交错三角格图ATm×(2m-2)(m≥2),记D(ATm×(2m-2))中围绕ATm×(2m-2)的外部面的6m-8 个顶点的在ATm×(2m-2)的外部面的6m-8 条短弧边依次为a1,a2,…,am=b2m-2,…,b2,b1=e1,e2,…,em=d2m-2,…,d2,d1=a1,见图5(左).

图5 (左)D(ATm×(2m-2))的6m-8 条短弧边.(右)D(AT4×6)的分支C1 和C4Fig.5 (left)(6m-8)small segments of arcs of D(ATm×(2m-2));(right)The components C1 and C4 of D(AT4×6)
注意到,4 条短弧边ai、b2i-2、ei和d2i-2属于D(ATm×(2m-2))的同一个分支Ci(2≤i≤m),其余的短弧属于D(ATm×(2m-2))的分支C1,且Ci两两不同(i=1,2,…,m).而且,ATm×(2m-2)的每条边被这些Ci的1 条或2 条恰好穿过2 次.故μ(D(ATm×(2m-2)))=m.
图5(右)粗线和虚线分别为D(AT4×6)的分支C1和C4.
3 交错三角格图ATm×n(2≤m≤4)的链环分支数
本节研究并证明交错三角格图ATm×n(2≤m≤4)的链环分支数.
引理5设m,n 是正整数,m≥2,n >2m-1,则μ(D(ATm×n))=μ(D(ATm×(n-2m+1))).
证因m≥2,n >2m-1.将ATm×n分离为ATm×(2m-2)和G12 个图.由引理3 和定理1 知,μ(D(ATm×n))=μ(D(G1)).又G1可经平图的R-变换变换为G2,见图6,由引理1 知μ(D(G1))=μ(D(G2)).因图G2经垂直翻转180°变换为ATm×(n-2m+1),又平图的垂直翻转变换不改变其所对应的链环图,故保持其链环分支数不变,所以μ(D(G2))=μ(D(ATm×(n-2m+1))).因此μ(D(ATm×n))=μ(D(ATm×(n-2m+1))).

图6 ATm×n(m≥2,n >2m-1)分离为ATm×(2m-2)和G1,G1 变换为G2Fig.6 ATm×n(m≥2,n >2m-1)is split to ATm×(2m-2) and G1,G1 is transformed to G2
推论1设m,n 是正整数,m≥2.若n=2m-2(mod 2m-1),则μ(D(ATm×n))=m.
证因m,n 是正整数,m≥2,n=2m-2(mod 2m-1).设n=(2m-1)q+(2m-2),(q 是非负整数).由引理5 和定理1 知,μ(D(ATm×n))=μ(D(ATm×((2m-1)q+(2m-2))))=μ(D(ATm×(2m-2)))=m.
引理6设m,n 是正整数,m≥2.若n=0(mod 2m-1),则μ(D(ATm×n))=1.
证因m,n 是正整数,m≥2,n=0(mod 2m-1).则n-1=2m-2(mod 2m-1).将ATm×n分离为ATm×(n-1)和G12 个图.由推论1 知μ(D(ATm×(n-1)))=m.由引理3 知μ(D(ATm×n))=μ(D(G1)).易知μ(D(G1))=μ(D(O1))=1.故μ(D(ATm×n))=1,(m≥2,n=0(mod 2m-1)).
定理2设n 是正整数.则
证对正整数n 用归纳法证明.当n=1 时,1=1(mod 3),μ(D(AT2×1))=μ(D(P2))=1.当n=2 时,2=2(mod 3),由定理1 知μ(D(AT2×2))=2.当n=3 时,3=0(mod 3),由引理6 知μ(D(AT2×3))=1.故当n=1,2,3 时,结论成立.假设对于所有的n≤k(k≥3,k 为正整数),结论成立.则当n=k+1 时,由引理5,知μ(D(AT2×(k+1)))=μ(D(AT2×(k-2))).由归纳假设知又k+1=(k-2)(mod 3),故根据归纳法原理,定理2成立.
显然有,
(1)AT3×i(i=1,2,3)都可经平图的R-变换变换为O1,由引理1 和2 知μ(D(AT3×i))=1(i=1,2,3).由定理1 知μ(D(AT3×4))=3.由引理6 知μ(D(AT3×5))=1.
(2)AT4×i(i=1,2,3,4,5)可经平图的R-变换变换为O1,由引理1 和2 知μ(D(AT4×i))=1(i=1,2,3,4,5).由定理1 知μ(D(AT4×6))=4.由引理6 知μ(D(AT4×7))=1.
由上述(1)和(2),并根据归纳法原理和引理5,仿定理2 的证明,可证明下面的定理3 和定理4 成立.
定理3设n 是正整数.则
定理4设n 是正整数.则
4 交错三角格图ATm×n(m≥2)的链环分支数的一个假命题
基于定理2~4,猜想交错三角格图ATm×n(m≥2)的链环分支数如下.
命题1设m,n 是正整数.若m≥2,则
我们将构造反例证明命题1 不真.
引理7[7]设m 是正整数,则μ(D(Lm×m))=m.
命题1不真的证明 由引理5、推论1 和引理6 知,命题1 与“命题※:设m,n 是正整数.若m≥2 且n≤2m-3,则μ(D(ATm×n))=1”同真假.由定理2 知μ(D(AT2×5))=2.又AT2×5可经平图的R-变换分别变换为图F1,见图7.将图F1与图L3×3之间按图7所示连以3 条边,得图F2.又F2可经平图的R-变换变换为图AT5×5,见图7.由引理1、3 和7,知μ(D(AT5×5))=μ(D(F2))=μ(D(F1))=μ(D(AT2×5))=2.但5 <2×5-3.故AT5×5是命题※的反例.故命题1 不真.
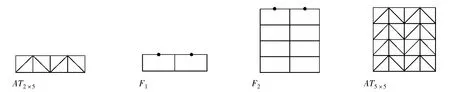
图7 AT2×5变换F1,F1 与L3×3之间连以3 条边得F2,F2 变换AT5×5Fig.7 AT2×5 is transformed to F1,F1 and L3×3 are connected to three sides to obtain F2,F2 is transformed to AT5×5
不难证明,AT(2+3t)×5(t 是正整数)是命题1 的一簇反例.
致谢:作者的导师金贤安老师提出了格图的链环分支数问题,并对本文的研究提出了许多宝贵建议.作者在此表示感谢!
[1]MURASUGI K.Knot theory and its applications[M].Boston:Birkhauser,1996:34-39.
[2]SHANK H.The theory of left-right paths[J].Combinatorial Math.Ⅲ,Lecture Notes in Mathematics,1975,452:42-54.
[3]PISANSKI T,TUCKER T W,ZITNIK A.Straight-ahead walks in Eulerian graphs[J].Discrete Math,2004,281(1-3):237-246.
[4]JIN X A,DONG F M,TAY E G.On graphs determining links with maximal number of components via medial construction[J].Discrete Appl Math,2009,157(14):3099-3110.
[5]ENDO T.The link component number of suspended trees[J].Graph Combinator,2010,26(4):483-490.
[6]LIN Y F,NOBLE S D,JIN X A,et al.On plane graphs with link component number equal to the nullity[J].Discrete Appl Math,2012,160(9):1369-1375.
[7]JIN X A,DONG F M,TAY E G.Determining the component number of links corresponding to lattices[J].J Knot Theor Ramif,2009,18(12):1711-1726.
[8]JIANG L P,JIN X A,DENG K C.Determining the component number of links corresponding to triangular and honeycomb lattices[J].J Knot Theor Ramif,2012,21(2),1250018-1250031.
[9]MPHAKO E G.The component number of links from graphs[J].Proc Edinb Math Soc,2002,45(3):723-730.
[10]汤自凯,侯耀平.恰有两个主特征值的三圈图[J].湖南师范大学学报自然科学版,2011,34(4):7-12.
[11]袁名焱,罗秋红,汤自凯.由星补刻画的一类广义线图[J].湖南师范大学学报自然科学版,2012,35(1):13-20.
[12]JIANG L P,JIN X A.Enumeration of left-right paths of square and triangular lattices on some surfaces[J].数学研究,2011,44(3):257-269.
[13]陈 红,梁文忠,许成章,等.刻画NP-C 问题复杂程度的一个模型——对计算Paley 图团数的实践做出预测[J].湘潭大学学报自然科学版,2011,33(4):7-11.
[14]NOBLE S D,WELSH D J A.Knot graphs[J].J Graph Theory,2000,34(1):100-111.
