GaN_Si npn HBT 特性研究
2013-12-22董果香李建清
董果香,李建清
(电子科技大学物理电子学院,成都610054)
GaN 半导体材料作为新型宽禁带材料,在光电领域和高功率高频电子器件方面有很大的应用[1]。在现有的工艺条件下,GaN 单晶尺寸很难生长较大,GaN 器件多以蓝宝石或SiC 为衬底[2]。GaN 与蓝宝石之间晶格失配达到15%,并且蓝宝石是绝缘材料,本身不导电,导热性差且与GaN 热膨胀系数差异较大。虽然SiC 衬底与GaN 之间晶格失配为3.5%,但SiC 材料加工困难且价格较为昂贵,这些原因限制了SiC 衬底的应用开发。Si 衬底和上面两种衬底相比,除了晶格失配和热失配较大外,具有质量高、尺寸大、成本低、导电性好等优点,并且Si 具有成熟的工艺,采用Si 作为GaN 基器件的衬底,可以将GaN 基器件集成到传统Si 基器件工艺中,因此Si 被认为是较为理想的GaN 衬底材料。随着在Si衬底生长GaN 单晶薄膜,GaN 基材料与器件有了较大发展[3-4],Si 衬底GaN 基光电器件研制引人注目。
GaN/Si/Si 双极晶体管的发射结为异质结,比同质结具有更高的注入效率,产生了许多优良的性能,例如具有更高的载流子调制能力和更低的导通电阻。在HBT 掺杂分布中,基区掺杂大于发射区掺杂。高的基区掺杂带来了许多优点[5-6]。首先,低的基区电阻提高了截至频率,改善了电流集中。更高的基区掺杂也提高了Early(人名)电压,减小了大电流效应。低的发射区掺杂也带来了诸如禁带变窄的减小以及Cbe 降低等好处。本文利用Silvaco 软件对平面GaN/Si/Si-HBT 特性进行了仿真。
1 器件结构及物理模型
器件模拟以器件物理工作机理和合理高效准确的数值算法为基础,它是研究和预测器件性能的重要工具。本文采用Silvaco 软件,它能够仿真特定结构和偏压下半导体器件的物理性能,使用户更好的理解器件内部工作机理[7]。
本文所研究的GaN/Si/Si-HBT 结构如图1 所示,由于GaN 的禁带宽度比Si 的禁带宽度大得多,所以可使发射区掺杂浓度低于基区掺杂浓度。发射区和基区都是采用均匀掺杂,发射区掺杂为5×1018cm-3,宽度为0.15 μm,基区掺杂为2×1019cm-3,宽度为0.1 μm,结深为0.01 μm。集电区为带N-外延层的N+衬底,外延层厚度为0.5 μm,掺杂浓度为5×1016cm-3,衬底厚度为0.15 μm,掺杂浓度为2×1019cm-3。此结构是按照Si 衬底GaN 基材料垂直工艺水平所设计,使器件的各项性能达到最佳。
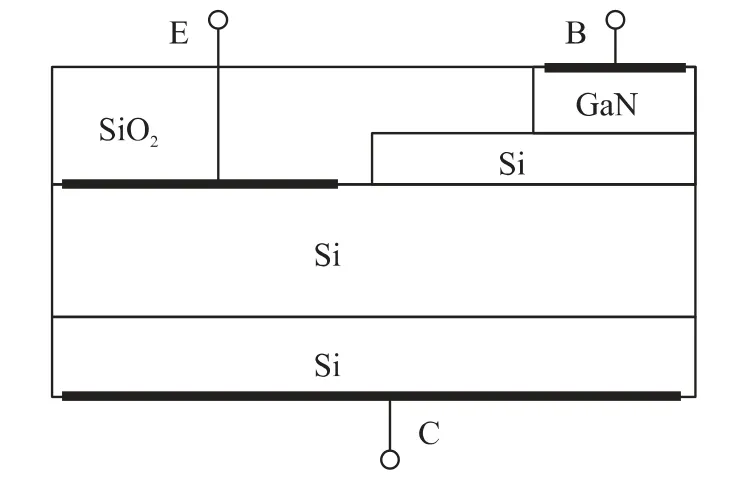
图1 HBT 器件结构
在模拟之前应对材料进行合理的建模,正确的模型是模拟的基础,包括能带模型,迁移模型,复合模型等,其中对GaN 和Si 的物理模型参数均来自最新的文献和试验结果。
在Silvaco 软件中BLAZE[8]模拟器可对各种特殊器件和材料进行模拟,包括HBT,HEMT,LED。对HBT 模拟时,必须明确两种材料导带和价带差异,即ΔEC和ΔEV。如果用户不指明,则软件默认为ΔEC=X1-X2和ΔEV=ΔEg-ΔEC。本文模拟选用默认值,其中X1是窄禁带材料电子亲和能,X2是宽禁带材料电子亲和能,ΔEg是两种材料能带差。
首先考虑不完全电离:
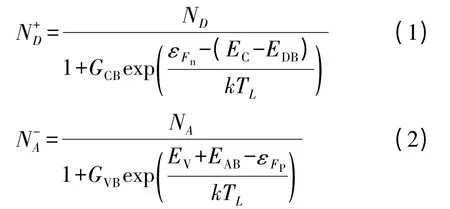
对于Si 和GaN 材料区域以上公式中各参数相同,参数值如下:GCB= 2,GVB= 4,EDB= 0. 044 eV,EVB=0.045 eV。
GaN 的能带模型为:
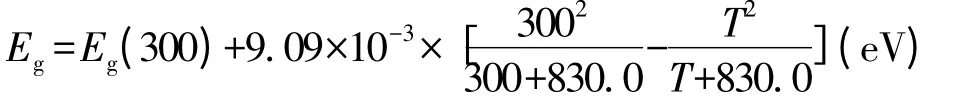
其中,T 是温度,单位为K,
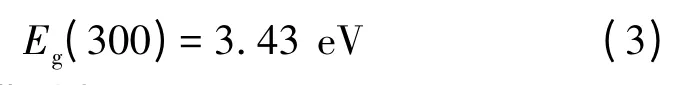
Si 的能带模型为:
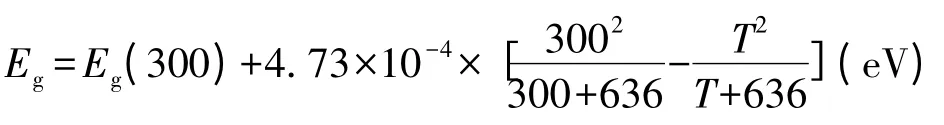
其中,T 是温度,单位为K,
GaN 的价带和导带有效状态密度NV和NC分别为2.51e19 cm-3和2.24e18 cm-3。Si 价带和导带有效状态密度NV和NC分别为1.04e19 cm-3和2.8e19 cm-3。
迁移率模型[9]对器件的研究十分重要,本文中迁移率模型为Silvaco 中的低电场迁移率模型中的恒迁移率模型和反型层迁移率模型FLDmob 的组合使用。
低电场恒迁移率模型为:
在Si 材料区中:在室温下,对于电子mμn=1 000,tμn=1.5;对于空穴:mμp=500,tμp=1.5。
在GaN 材料区中:在室温下,对于电子mμn=400,tμn=1.5;对于空穴:mμp=8,tμp=1.5。
而FLDmob 迁移率模型为:
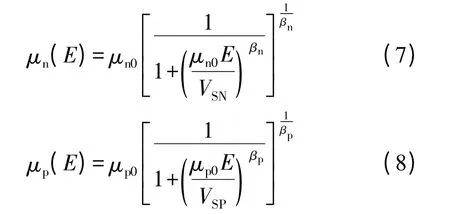
在Si 材料区中对饱和速度VSn和VSp作如下修正,其中饱和速度如下[10]:
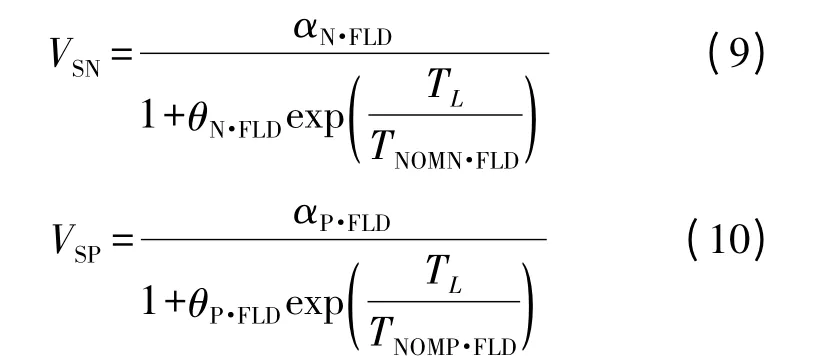
其中TNOMN·FLD=TNOMP·FLD=600 K。
以上各参数都有确定的值,其值请参考Silvaco用户手册chapter 3 Physics P115。
在GaN 材料区中直接给出饱和速度vSN=1.91×107cm/s,vSP=1×106cm/s
复合模型[11]为SRH 模型:
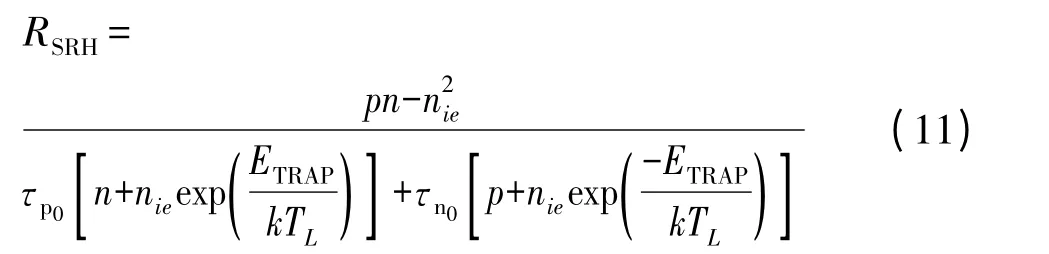
其中Si 的少数载流子寿命τp0=τn0=1×10-7s 由于GaN 少数载流子寿命相关材料未有精确值,所以全部设为与Si 的少数载流子寿命相同。其中ETRAP=0 eV。
2 结果及分析
如图2 所示,发射区是宽禁带,基区和集电区为窄禁带。发射结为异质结,由于价带的不连续性大于导带的不连续性,所以基区空穴注入效率小于发射区电子注入效率,HBT 电子注入效率和电流增益大幅提高。其中ΔEC=1.65 eV,ΔEV=1.70 eV。
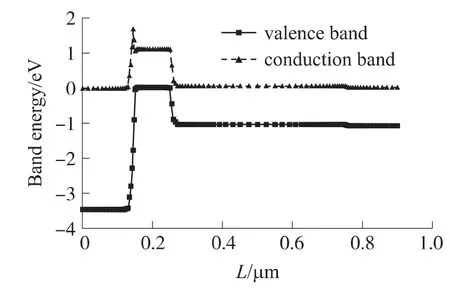
图2 HBT 能带结构图
图3 是器件在Vce=3.6 V 时,器件的Gummel曲线,因为采用了GaN/Si 异质结,GaN 的禁带宽度较大,所以器件导通压降大约为2.5 V,大于采用Si的同质结的0.7 V。当Vbe>2 V 时,发射结趋于导通,HBT 趋于放大状态,Vbe继续增大,发射结导通,HBT 处于放大状态。从图中还可看出,在Vbe较大变化范围,电流增益几乎是一个常数。当Vbe>3 V时,由于大注入造成的基区变宽和电流集边,使Ib和Ic趋于饱和。
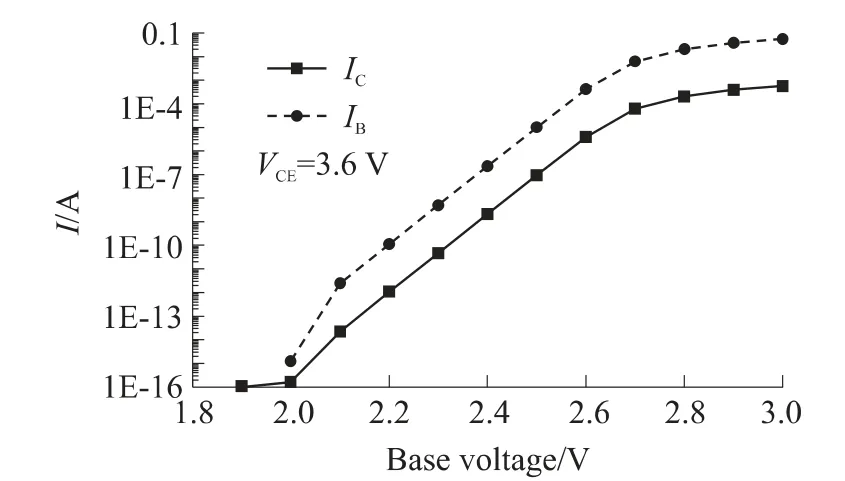
图3 当Vce=3.6 V 时HBT 的Gummel 曲线
在仿真输出特性曲线时,对基极采用电流控制,基极电压大约在1.2 V。当集电极电压从0 V 开始增大,由于Vb=1.2 V,所以集电结导通,发射结关断,所以集电极上增加的电压大部分落在在发射结上,使发射结上电压上升。当Vce=1.8 V 左右,落在发射结上的电压大于发射结开启电压,发射结导通。集电极电压继续增大,HBT 先后进入饱和区和发大区。所以如图4 所示观察到Vce=1.8 V 时,集电极电流明显上升,即输出特性具有一定的开启电压,较大的开启电压,增大了器件的功耗,降低了HBT 输出电压摆幅。当Ib=2×10-4A 时,Ic大约是0.02 A,增益大约为100 倍。
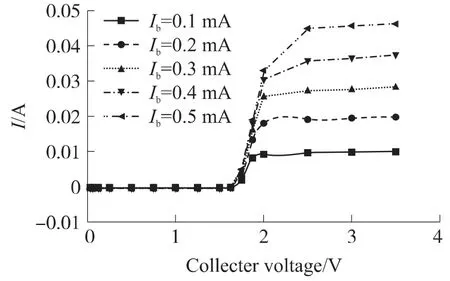
图4 共射极输出特性曲线
从图5 可以看出器件的击穿电压大约为900 V左右,远大于Si 晶体管的击穿电压,这是由于采用异质结的缘故,可见宽禁带发射区HBT 在功率器件方面用很大应用前景。如果采用双异质结晶体管,即DHBT,在击穿电压方面有更进一步的提高,但是由于基区和集电区导带不连续形成的势垒,对基区电子到集电区漂移产生较大影响,这个问题需要考虑。
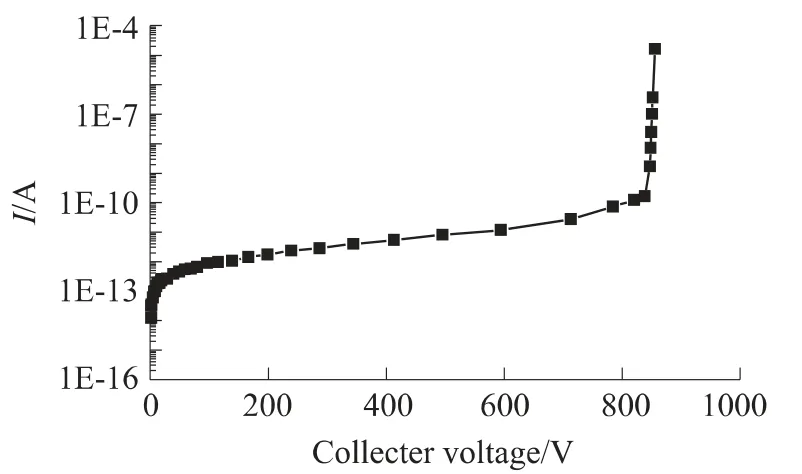
图5 器件击穿特性曲线
图6 是Vce=3.8 V,Vb=3.0 V 下得到的,最大增益为39.3 dB,随着频率的上升,增益保持不变,当频率为1 GHz 时,增益开始下降,当频率为80 GHz 时,增益为0 dB。频率从0 Hz 到1 GHz,增益一直保持39.3 dB,具有较宽的频带宽度。此器件可工作在射频频段。

图6 电流增益随频率变化
图7 表明了器件截止频率随工作电流的变化关系。在集电极电压恒定时,ft 最开始随电流Ic增加而上升,达到极大值后,再随着Ic的增加而下降。开始随着电流Ic增加ft 上升,这正好符合双极晶体管截止频率计算公式中延迟时间与电流关系。当电流进一步增大到超过某一临界值后,大电流下的基区变宽效应使基区渡越时间增加,从而导致ft 减小。
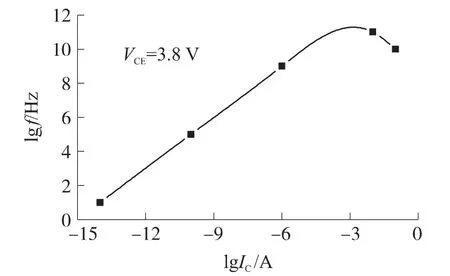
图7 HBT 的截止频率随频率变化
3 结论
本文用器件模拟软件Silvaco 模拟了GaN_Si HBT,详细列举了模拟所用的物理模型和参数,包括能带模型,迁移率模型,复合模型等。得出了器件能带结构,Gummel 曲线,输出特性曲线,击穿电压和截止频率并对对器件的物理机理作出了解释和分析。由于目前还没有GaN_Si HBT 研究报道,本文对其进一步理论研究和器件制造具有指导意义,而且对Si衬底GaN 基器件的发展具有较大指导意义。
[1] 滕晓云.Si 衬底GaN 基材料及器件的研究[J]. 半导体技术,2006,31(2):98-107.
[2] 陈鹏.Si 基GaN 外延生长[J]. 固体电子学研究与进展,1999,19(2):200-202.
[3] 李炜.Si 表面吸附GaN 的第一性原理[J].材料导报:研究篇,2009,23(8):71-77.
[4] 颜怀跃. Si 衬底上GaN 厚膜生长及Cr 掺杂GaN 性质研究[D].南京:南京大学物理学院,2011.
[5] 施敏,伍国钰.半导体器件物理[M].西安:西安交通大学出版社,2010.
[6] 高金明,李圭. 高频异质结晶体管直流和交流模型及其验证[J].电子器件,2011,34(2):133-135.
[7] 吉利久.计算微电子学[M].北京:科学出版社,1996.
[8] Apanovich Y.Numerical Simulation of Submicrometer Devices,Including Coupled Non-Local Transport and Non-Isothermal Effects[J].IEEE Trans.Electron Devices,1995,42(5):890-898.
[9] Klaassen D B M. A Unified Mobility Model for Device Simulation[J].Solid-State Electronics,1992,35:953-959.
[10] Canali C G,Magni R Minder,Ottaviani G.Electron and Hole Drift Velocity Measurements in Silicon and Their Empirical Relation to Electric Field and Tempratrue[J]. IEEE Trans. Electron Devices ED,1975,22:1045-1047.
[11] Law M E.Self-Consistent Model of Minority-Carrier Lifetime,Diffusion Length,and Moblity[J].IEEE Electron Device Letters,1991,12(8):256-261.
