阵列天线收发隔离技术

张焕斌，汪立新

(杭州电子科技大学通信工程学院，杭州310018)

自适应滤波包括自适应时域滤波，自适应空域滤波等。它和信息论、优化理论、检测与估计理论等密切相关，是近三十年来发展起来的信息科学的一个重要分支，并在通信、雷达以及许许多多领域获得了广泛的应用［1］。自适应滤波器的运作机制可以归纳为以下几个步骤:(1)当滤波器在输入过程中的统计特性未知时，它能够调整自己的参数，从而达到某种最佳准则的要求，这一过程被称为“学习过程”或者“训练过程”;(2)当输入过程的统计特性变化时，滤波器将再次调整自己的参数，该过程被称为“跟踪过程”。

在对设备便携性越来越高的当今社会，任何设备都需要减小本身对硬件资源的消耗。在阵列天线中，接收端将会有多路信号同时进入设备，有一种最简单的方法就是在每一路信号中加入一个回波抵消模块，然而这样对硬件资源的消耗是不言而喻的，本文将在16 路信号输入的阵列天线平台上只加入一个回拨抵消模块来达到提高收发隔离的目的。

1 阵列天线收发隔离技术原理

1.1 阵列天线收发隔离系统模型

同频信号收发隔离系统模型如图1 所示(注:图中的两个PN 码实际上是同一个信号源发出，为了使框图更加简洁将它分为两个地方表示)从传来的有用信号通过接收天线进入到模拟下变频，然后通过模数转换之后进入回波消除模块，回波处理结束以后再经过PN 码叠加，数模转换，模拟上变频，功率放大器，最后由发射天线发射出去。从图中可以看出信号由于经过了功率放大器的作用，使得发射信号的强度远大于远处传来的有用信号，而且发射信号与有用信号是同频的，所以同样会被接收天线所接收，将会产生回波干扰。如果不经过回波处理的话，有用信号将淹没在回波当中。因此，必须在系统中加入回波抵消模块来消除回波对有用信号的影响。

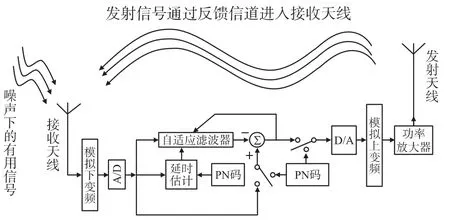
图1 同频信号收发隔离系统参考模型框图

回波消除模块的主要任务就是对反馈信道进行参数估计，计算出信号从回波消除模块输出端口到达回波消除模块的输入端这样一个过程中的幅度，时延参数，然后进行抵消处理。

1.2 自适应滤波器内部结构

通过图1 可以了解到，系统在进行自适应滤波之前会先对回波信号的延时进行估计，并且可以通过对PN 码进行延时处理达到与回波信号同步的效果。其中同步处理模块将用到一个RAM 作为缓存，它的结构如图2 所示，图中delay 是延时估计之后得到的延时值。

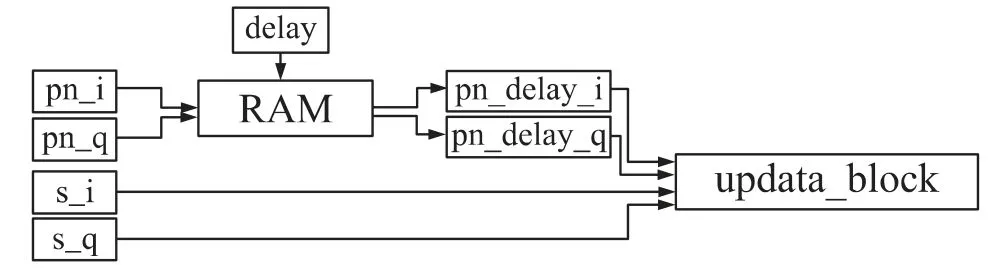
图2 同步处理模块流程图

在传统的自适应滤波器设计中会对信号进行延时处理，然后对不同延时量的信号与权系数相乘。结构设计如图3 所示。

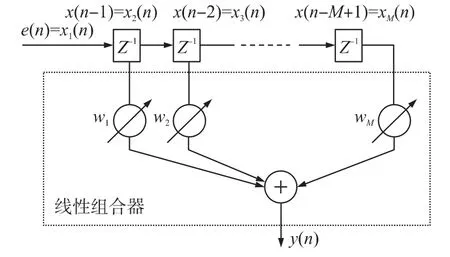
图3 自适应滤波器的直接型结构

阵列天线本身的具有一个特点:16 路信号接收的是同一个信号，但是在时间上有前后的极细微差别。根据这个特点，可以假设每两路相邻信号之间的码片间隔是m，第1 路到第16 路的信号分别为x1(n)，x2(n)…x16(n)，那么x1(n)= x2(n－m)=x3(n－2m)=…=x16(n－15m)，可以看出，这当m=1 时，这16 路信号所组成的信号就是传统自适应滤波器所需要经过延时处理以后的输入信号。根据自适应算法的根本原理:由序列的一组连续值向前估计一个值，所以对于m 的取值理论上是任意的，但由于阵列天线之间的距离只是厘米级别，因此m 的值会很小，从而非常接近传统自适应滤波器。

当对每1 路滤波器加上1 个只有一阶的权矢量的时候，通过对16 路信号的整合就变成了1 个类似16 阶的自适应滤波器，具体的结构如图4 所示，图中最下面的x(n)表示每一路通道所对应的输入信号。在权矢量更新部分，相当于将传统滤波器中w和x 的矢量相乘分拆成16 个单独的w 与x 的标量相乘。最终将每个自适应滤波器的误差信号进行筛选，筛选出误差最小时的那个权值，这个权值就是最佳权矢量中的最大权值。

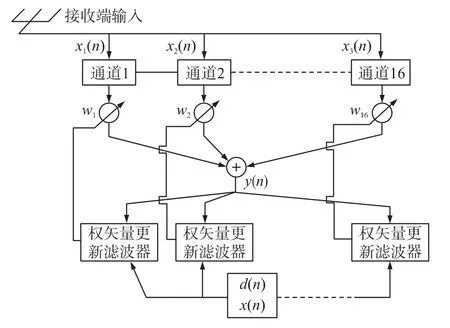
图4 阵列天线自适应滤波器结构图

根据研究，自适应滤波器的最佳权矢量中，会有一个值特别大，由此可以判断，在抵消过程中，主要是由这个值所加权后的信号与回波信号进行抵消，所以提出一个方案:利用这个权值来代替整个权矢量以此来减少计算量，但这也不可避免地降低了抵消效果。进一步的研究发现，被降低的抵消效果是微乎其微的。式(1)中展示的是一个32 阶滤波器最终得出的最佳权矢量，其中实验设置的回波信号是有用信号的100 倍。观察式中数据可以发现第14 个权值是99.999 999 171 113 6，极其接近理想状态下的100，而其余的权值大小的数量级均在10－7以下，所以用一个最佳权矢量中的最大值来代替整个权矢量的方法在理论仿真中是可行的。

假设都是用16 阶滤波器，都是采用固定步长的LMS 算法，新方法在计算量中与传统结构的比较如表1 所示，从表中可以明显看出新方案在阵列天线的应用上的优势，它将极大的减少计算量，减少对硬件资源的消耗。

表1 新老方法计算量对比

1.3 算法理论

通过之前的研究分析，减少算法复杂度，降低硬件消耗对于阵列天线收发隔离技术是非常重要的。降低算法复杂度意味着降低了算法性能。在当前自适应算法研究非常深入的今天，寻找到一种能够保证算法性能的前提下尽可能的降低算法复杂度成为了在阵列天线应用中对算法的一个标尺。

1.3.1 变步长算法研究概述

在当前的自适应研究中，步长因子起到一个很重要的作用。简要来讲就是当步长因子太大时可以使收敛速度增快，但是稳定性很差，引起过渡过程的振荡;反过来，如果步长因子太小，可以保证整个过程的稳定以及收敛，但是收敛速度太慢。针对这个矛盾，不少学者提出了变步长最小均方误差算法。首先回顾一下最原始的最小均方误差(LMS)算法。

假设输入信号是x(n)，加权矢量为w(n)，如式(2)、式(3)所示:

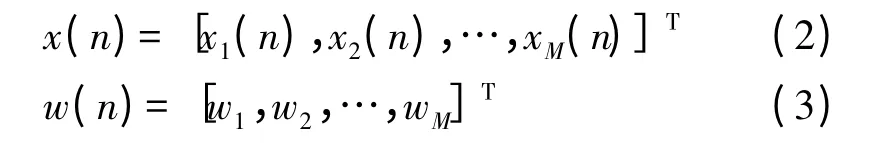
滤波器输出为y(n)，误差信号为e(n)，其表达式如式(4)、式(5)所示

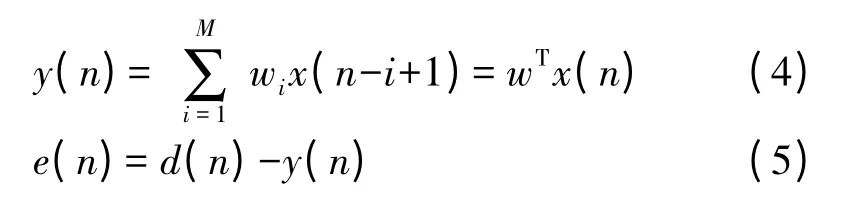
其中d(n)就是我们所期望得到的期望信号，LMS 算法就是使e(n)的均方值最小，最终得出加权矢量的递推公式如式(6)所示:

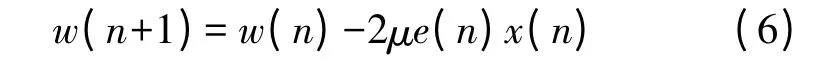
以上是原始LMS 算法的简单介绍，其中μ 是一个常数，这也导致了前文提到的稳定性与收敛速度的矛盾。变步长LMS 算法这个概念的提出就是通过让步长因子变成一个变量，使得在滤波初始阶段的收敛速度变快，但到了稳态以后减小步长因子的大小以提高算法稳定性。

在过去对变步长LMS 算法的研究总结中可以大概分为3 种类型:(1)根据滤波器输出的误差信号，建立其误差信号与步长因子之间的函数关系;(2)建立步长因子与自适应滤波过程中的梯度向量之间的函数关系;(3)基于不同最优准则的最优变步长LMS 算法。这些不同类型的变步长LMS 算法在不同的滤波环境中都有着不俗的表现。首先了解一下后面2 类方案中的典型算法。

1.3.2 基于梯度向量的变步长LMS 算法分析

建立步长因子与自适应滤波过程中的梯度向量之间的函数关系的典型算法是1989 年Karni 提出的［8］，他的算法表达式如式(7)、式(8)所示:

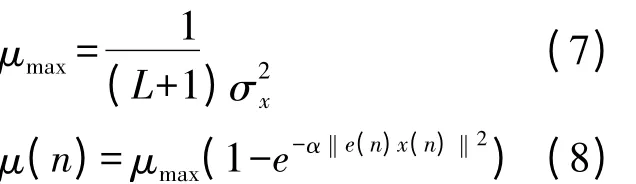
μmax是保证LMS 算法收敛情况下的最大步长，它的引入可以保证变量μ(n)在变化过程中算法的稳定性。但是它将涉及到模运算以及指数不是整数的指数运算，这将造成对硬件资源的依赖性增加;其次在对参数α 取值对算法性能的影响非常大，而α 在选取过程中完全依靠经验来获得。所以该算法不适用本次研究的需求。

1.3.3 基于某些最优准则的变步长LMS 算法分析

第3 类变步长算法的典型案例是Shin 在2004年提出来的一种算法，他的算法表达式如下:

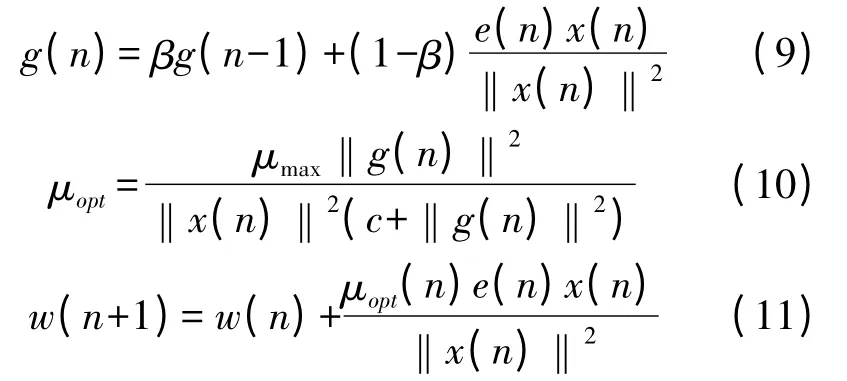
在文献［12］中提到该算法只能在低噪声环境下应用，当处于高噪声环境下的时候式(9)将会产生较大的偏差，极大的影响算法性能。而且它的计算量相比Karni 提出的算法更大，因此也不适用于本次研究的需求。

1.3.4 基于误差信号的变步长LMS 算法分析

在排除了后面两类变步长LMS 算法方案之后再来了解第1 类算法的性能，并通过其与固定步长LMS 算法在收敛速度，稳定性，额外均方误差方面做对比。其中额外均方误差是在自适应研究中很多学者都会用到的一个参数，它的引入是为了避免外部噪声所造成的影响，其表达式如式(12)所示:

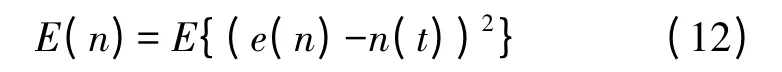
在基于误差信号的变步长LMS 算法研究中的典型算法是Kwong 在1992 年提出来的［9］，它的表达式非常简单:

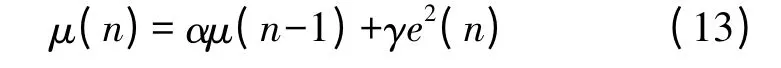
由于算法初始阶段，误差信号相对来说会非常大，利用误差信号作为步长因子的变化梯度可以使步长在初始阶段的值很大，从而提高收敛速度;当权矢量趋于平稳以后，误差信号也趋于最小值(理想状态下是0)，步长因子也会趋于平稳。

文献［9］中提到α 是在区间(0，1)上取值的，通常会取0. 97，但是在笔者做仿真试验过程中认为0.985 比较合适，在下面会进行两者的比较;γ 的取值会根据不同环境下来选取不同的值，但通常会是一个很小的值。

首先，对α 的取值进行对比，图5 中γ 的取值为10－8，对α 分别取0.900，0.970，0.985 3 个值进行比对，设置的理想权矢量为100。从图中可以发现α的取值影响着Kwong 算法的性能，虽然在不同取值中对收敛速度几乎没有影响，但是当算法稳定以后所得到的权矢量值与期望值有差别，总体来说α 越大，最终得到的权矢量值与期望值越接近，但到了0.985 以后，例如α 取0.990 时与0.985 的差别几乎没有，但是当取0.990 的时候容易引起算法在迭代过程中出现错误，如图6 所示。

确定α 的取值以后，将Kwong 算法与原始LMS

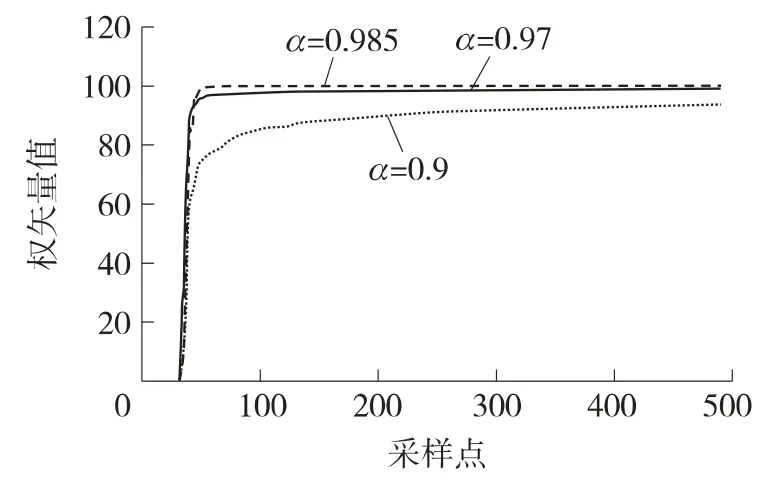
图5 采用不同α 值下的权矢量值

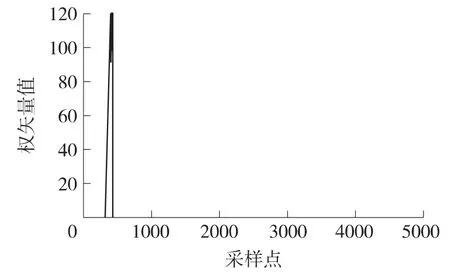
图6 当α=0.990 时会出现的错误现象

算法进行对比，如图7 所示。在同样的收敛速度下，原始LMS 算法在初期的不稳定性要高于Kwong 算法;在降低μ 值以后，权矢量可以做到平缓的收敛，但是收敛速度与Kwong 算法的差距也是很明显的。

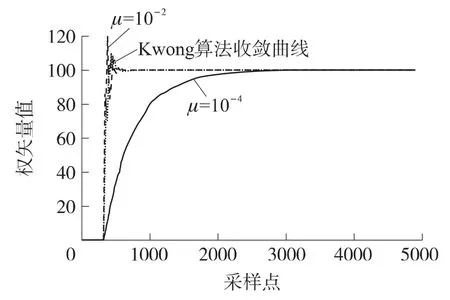
图7 Kwong 算法与原始LMS 算法的比较

2 性能测试

在本次测试过程中，在第1 步的训练过程添加了噪声因素以达到更加符合实际条件的目的，另外信号类型上采用的时BPSK 信号，其中信号采样频率为160 MHz，载波频率为50 MHz，训练序列频率为10 MHz，采样点数是5 000 点，训练序列的长度Pn_L 为127 个码片长度，假设信号功率为0 dBm，信噪比－20 dB，噪声在整个系统运行中是一直存在的，等效辐射功率为40 dBm，即反馈信号的幅度是有用信号的100 倍;仿真延时为32 μs。

2.1 延时估计性能测试

第1 节中提到在运用新模型结构做自适应滤波之前会对整个系统的回波延时做一个估计然后进行同步处理。延时估计过程通过对延时估计的两个输入x(n)与P(n)之间进行如下运算:

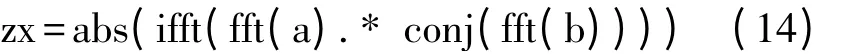
式中的a 代表空间回波输入x(n)，b 代表本地PN码输入P(n)，运算结果存入二维数组zx 中，然后从中挑选出最大值，并记录它所在的位置，即延时时间。这种方法是根据发射信号与接收信号的相关性来计算出反馈信道的延时参数。在做完延时估计之后将延时时间输入到自适应滤波器中，利用这个参数将自适应滤波器的输入信号x(n)做一次同步处理，使得它能与P(n)同步。

首先在Matlab 上对延时估计进行性能测试，图8显示的时相关估计法得出的仿真图。从图中可以看出利用相关法得出的最大值是唯一而且明显的，这样保证了在进行延时估计时所得到的值能够准确无误。在得出相关值最高点的位置max_location 以后，经过式(15)的计算得出延时长度delay 的值。

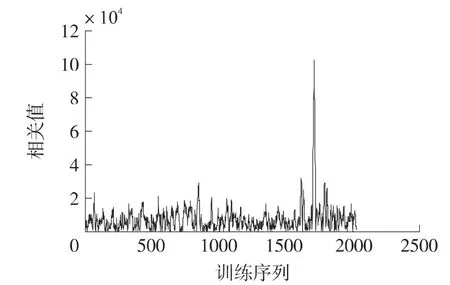
图8 各个采样点上的相关值分布情况

2.2 幅度估计性能测试

在幅度估计中有两个很重要量:权矢量和误差信号。前者主要观察其收敛速度及过渡过程的振荡特性，这在第2 节中已经有过详细的介绍以及与其他算法的比较就不多做介绍，本节主要展示对误差信号的测试情况。

图9 展示的是测试过程中的误差信号，在整个测试过程中并未加入有用信号，只是通过PN 码通过发射天线发射，然后通过接收天线接收到一个回波信号，最后作为回波信号输入进行自适应滤波，经过滤波以后得出的误差信号为零，表示自适应滤波器能够将回波信号全部抵消。

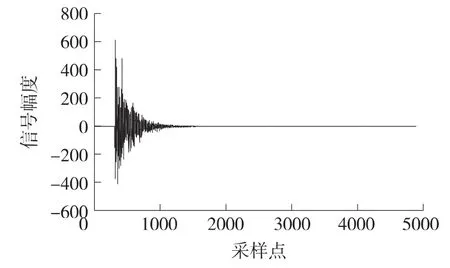
图9 误差信号

经过测试过程将得到反映整个回波通路幅度加权的权矢量，通过这个权矢量，再对实际应用过程的性能进行重新测试。在实际应用测试过程中，PN 码产生器不再产生信号，取而代之的是从接收天线输入一个有用信号来模拟真实环境，系统结构图如图10 所示。

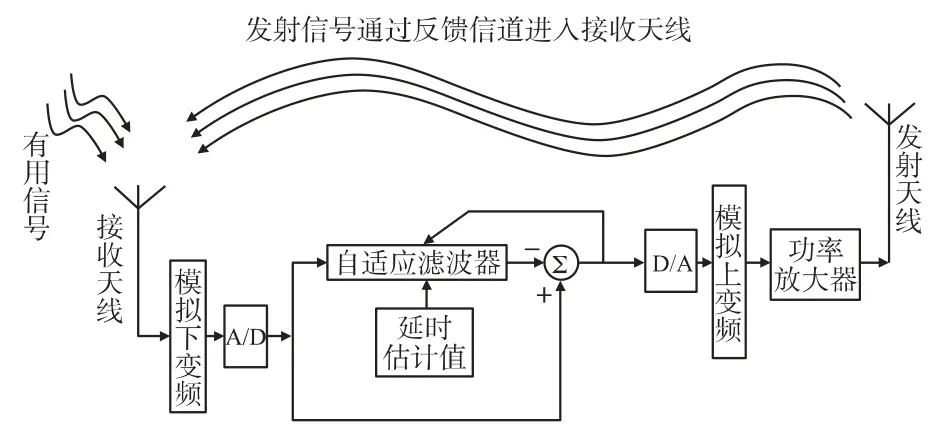
图10 回波消除模块在实际运行过程中的系统框图

在设计过程中，对自适应滤波器的输入端信号以及输出端信号分别与设计的有用信号进行相关处理，得出图11 和图12。

图11 抵消前信号与发射信号相关值

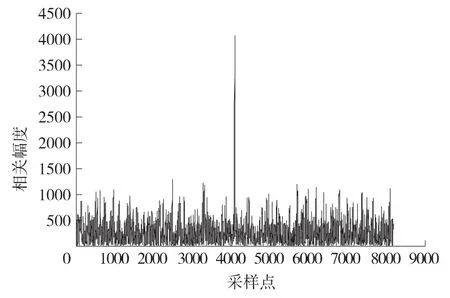
图12 抵消后信号与发射信号相关值

式(16)和式(17)分别给出了抵消前后信号的组成部分，x1表示抵消前的信号，s(t)是发射信号，echo(t)是回波信号，n(t)是噪声信号，根据第3 节的开头部分中的参数假设可知回波信号远大于发射信号，因此抵消前后的两个信号与发射信号做相关之后，他们的峰值位置会由所不同，抵消前信号与发射信号的相关峰会在回波信号echo(t)的位置上，抵消后信号与发射信号的相关峰会在发射信号s(t)上，它们之间的间隔就是回波信号信号经过整个反馈信道所产生的时间延时，从图中大致可以看出差别，具体数值经过对图11 和图12 的放大处理以后可知分别为3 769 和4 089，间隔距离为320，刚好符合假设中的延时值。

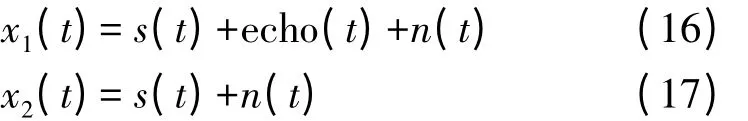
3 结束语

本文重点解决在阵列天线收发隔离技术上的计算量问题，根据阵列天线的多路通道相同信号的特点提出了并列型结构的自适应滤波器，避免了每路通道都配备一个单独滤波器的方法，有效的降低了系统计算量，减少了对硬件资源的消耗。

［1］ 赵知劲.自适应信号处理教材［M］.2 版.杭州电子科技大学编订.

［2］ 陈杰.MATLAB 宝典［M］.3 版.北京:电子工业出版社.

［3］ 何宾.Xilinx 可编程逻辑器件设计技术详解［M］.北京:清华大学出版社.

［4］ ［美］Samir Palnitkar. Verilog HDL 数字设计与综合［M］. 夏宇闻，胡燕祥，刁岚松，等译.北京:电子工业出版社.

［5］ 刘开健，吴光敏，张海波. LMS 算法的自适应滤波器FPGA 设计与实现［J］.仪器仪表与分析监测，2008(4):10－12.

［6］ 连瑞梅.一种改进的LMS Newton 算法及分析［J］.潍坊学院学报，2010，10(4):37－47.

［7］ 谢智波.自适应回波抵消器的算法分析与比较［J］. 浙江万里学院学报，2007，20(5):39－42.

［8］ Karni S，Zeng G. A New Convergence Factor for Adaptive Filters［J］.IEEE Trans.Circuits Syst，1989，36(7):1011－1012.

［9］ Kwong R H，Johnston E W. A Variable Step Size LMS Algorithm［J］.IEEE Trans on Signal Processing，1992，40(7):1633－1642.

［10］ Porat B.Second－Order Equivalence of Rectangular and Exponential Windows in Least－Squares Estimation of Autoregressive Process［J］.IEEE trans on signal processing，1985，33(5):1209－1212.

［11］ Paleologu C，Ciochina S，Benesty J. Variable Step－Size NLMS Algorithm for Under－Modeling Acoustic Echo Cancellation［J］.IEEE Signal Processing Letters，2008，15:5－8.

［12］ Shin H C，Sayed A H，Song W J.Variable Step－Size NLMS and Affine Projection Algorithms［J］. IEEE Signal Processing Letters，2004，11(2):132－135.