用三维抛物方程的CNFD 技术计算传播损耗*

任 明，钱志华

(杭州电子科技大学天线与微波技术研究所，杭州310018)

电波传播一直是工程电磁场理论和环境电磁特性研究领域中最为人们广泛关注和研究的方向之一。抛物型方程法是从Maxwell 方程组出发做前向传播近似，从而把椭圆型的波动方程简化为抛物型方程［1］。抛物型方程方法在精确预测电波传播路径损耗中得到了广泛的应用，使得电波传播数值计算有了新的突破。本文采用有限差分算法，可以直接计算出任意边界上的场，因此在处理不规则地形边界时比较方便，同时解决了大规模矩阵求解难的问题，为计算复杂环境下大尺度宽范围的电波传播损耗提供了一种有效方法。

1 抛物型方程的Crank－Nicolson 离散

本文设时谐场因子为e－jωt，电磁场分量在无源空间满足波动方程［1］:

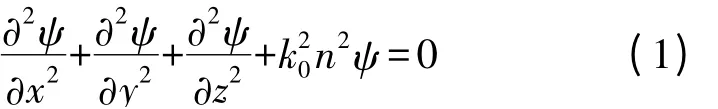
式中，k0，n 分别为自由空间波数和大气折射率。设想电磁波沿主轴(x 轴)方向传播，提取沿x 轴方向相位发生快速变化的这一项，即令u=e－jk0xψ，

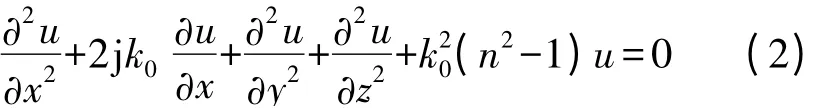
考虑到u 关于x 的二阶导数很小，忽略此项，式(2)就转换成标准的三维抛物型方程:

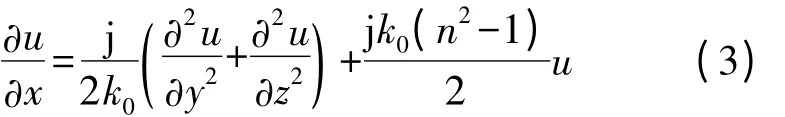
为了数值求解式(3)，我们采用Crank－Nicolson(CN)差分方案［2］。因此:

上标k 和下标m，n 分别是x，z 和y 方向上的位置示意，Δx，Δy，Δz 分别是x，y 和z 方向上的空间步长。代入式(3)，将关于k+1 和k 的项分别置于方程的两边，得到

不难发现，k+1 平面内的场可以通过k 平面的场递推得到。如果已知初始场，就可以借助相邻平面间场值的递推求出任意感兴趣平面上的场分布。定义UM×N为表征二维场点的矩阵，则式(4)可以表示成一般矩阵形式:

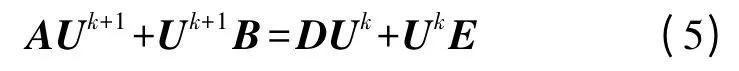
其中A，B，D，E 分别是如下所示的三对角方阵:

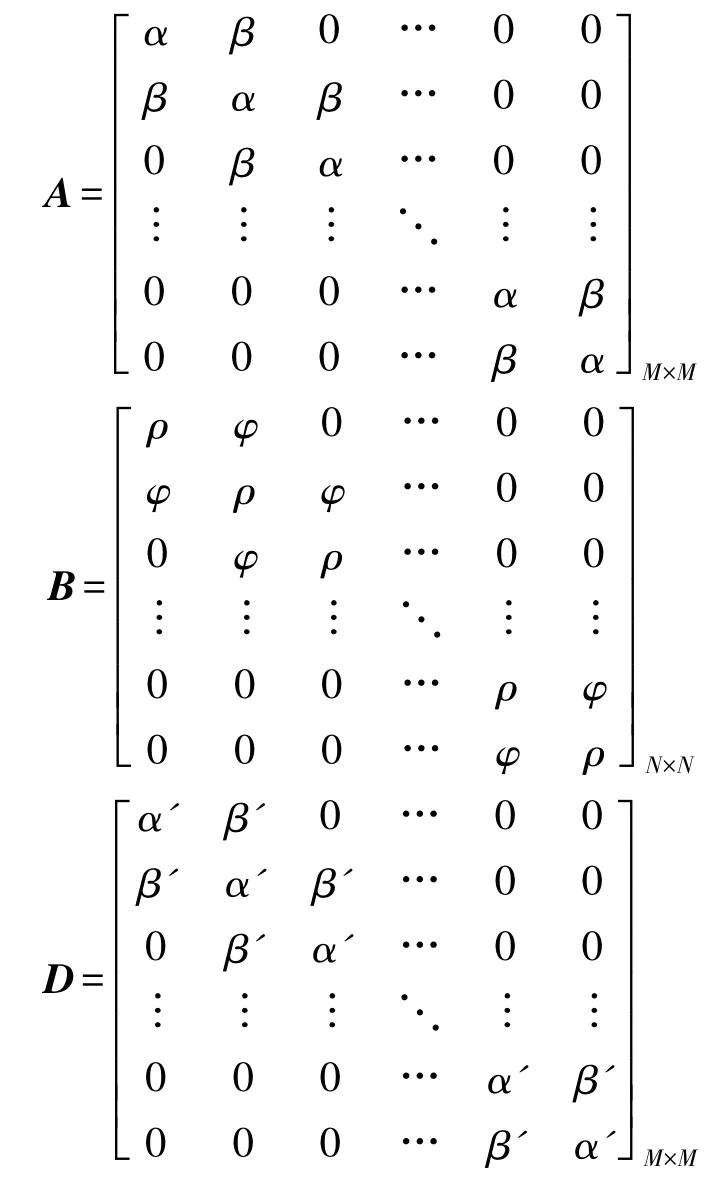
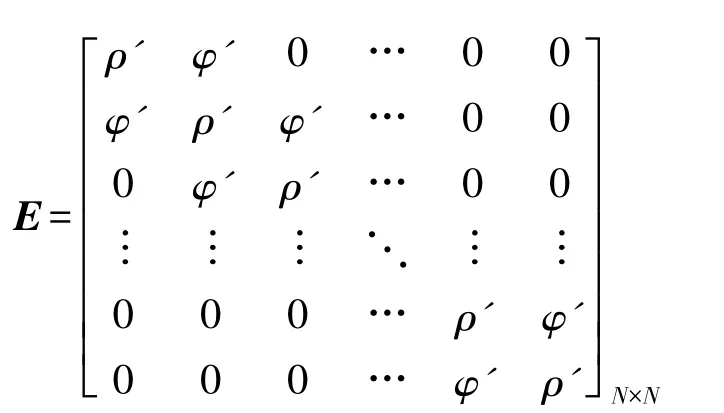
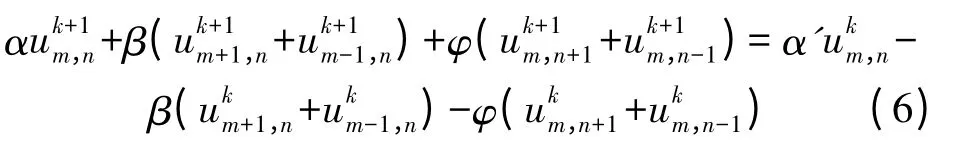
需要特别强调的是，式(6)只适用于完全位于离散区域内的场点。如图1 所示，意味着m 不能取－1 或M，n 不能取0 或N。因此，总的待求场点数实为M×(N－1)。为建立完整的求解方程组，还需结合初始场分布，以及地表边界条件、吸收边界条件经离散得到辅助方程。幸运的是，用有限差分法处理上述条件非常方便，详见后续内容。

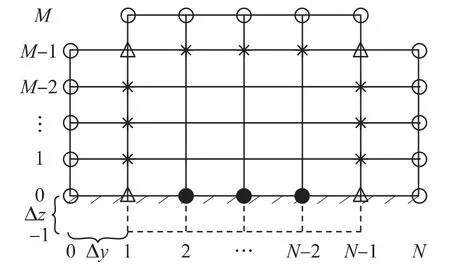
图1 二维场点的位置示意图

2 激励源

递推所需初始场由激励源产生，本文采用了高斯电流源。假设在初始距离处，电磁场分量由一个电流源J 辐射产生［3］:

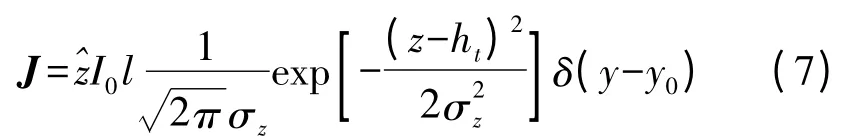
式中I0l 为电流矩(取1)，ht是发射天线的架设高度，σz决定着高斯方向图在z 方向的3 dB 波束宽度。δ(y－y0)是狄拉克函数，意味着天线的位置在y轴上的投影为y=y0。

3 吸收边界条件

3.1 列昂托维奇(Leontovich)地面边界条件

三维场的数值计算需要耗费巨大的计算机资源。因此，有必要对计算区域进行一定的限制。为此，在计算区域的截断边界处必须提供吸收边界条件。

图1 中处于m=0 的场点，应满足一定的空/地边界条件。电波传播区域的下边界通常并非理想导电平面，而是满足阻抗边界条件，又称列昂托维奇边界条件［4］。即

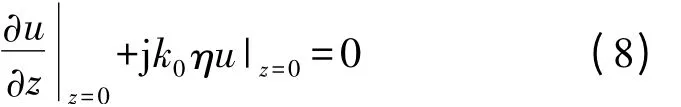
其中η 是归一化表面阻抗，它由地表面的相对介电常数和导电率决定，还取决电磁场分量的极化方式，利用地面下方的虚拟场点(见图1)以及中心差分思想，可将式(8)离散为:

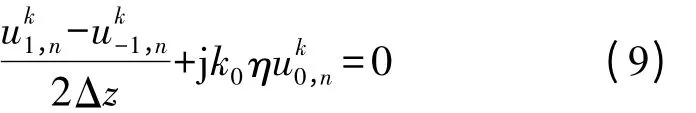
代入式(6)，消去虚拟场点项，得到波动方程融合地表作用后的差分方程:

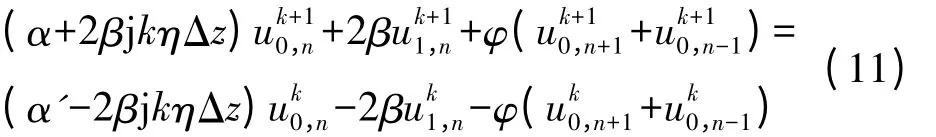
3.2 非局部吸收边界条件(NLBC)

这里介绍3DPE 方程离散算法常用的非局部吸收边界条件［2］。这种边界条件最大的好处是其占用辅助场点数较少，节约计算机存储单元。

不妨以计算区域顶部吸收边界条件为例，左右吸收边界条件的推导只需简单地交换坐标变量。借助拉普拉斯变换，严格按照文献［2］中的思路，可以得到:

在大气折射率n=1 的条件下，取φ1=22°，φ2=45°，NLBC 对电磁波的吸收效果最好。不难发现，式(12)涉及到卷积计算，其物理意义就是:在当前距离处，边界条件的满足依赖于所有以前距离处的场。

式(12)的离散借助辅助场点(图1 中标有“○”的点)，在相邻递推平面区间作卷积运算时将二阶导数项简单看作常数，即不随距离发生变化，并取作:

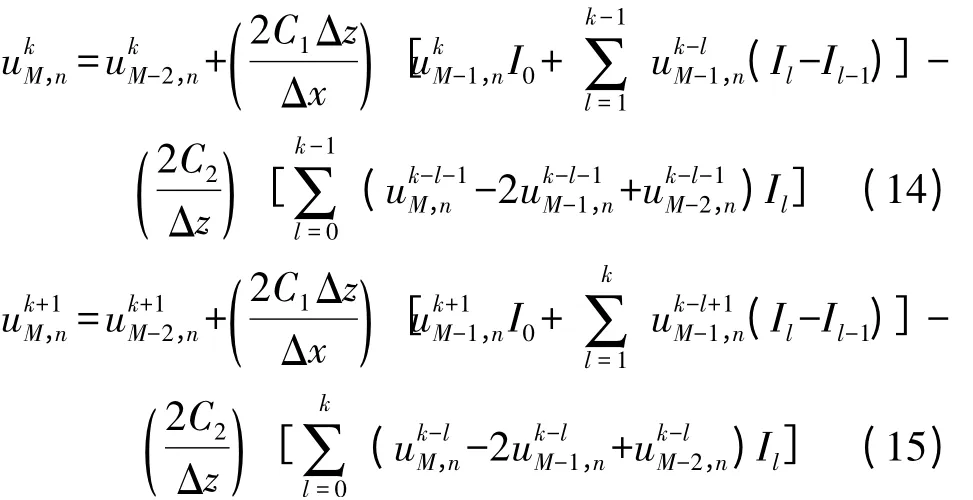
将式(14)、式(15)代入式(6)，最终得到顶部NLBC的差分方程:

遵循同样的思路，可以分别推导出左右边界处NLBC 满足的方程，注意左边界与右边界的方程之间差一个负号。需特别指出的是，在左右边界NLBC 方程中，常数将变为C3、C4(只需要将正弦改为余弦即可)。到此，图1 中标有“* ”的点满足的差分方程就全部推导完毕。由于场点分布呈二维矩形，图1 中“Δ”的4 个角点，它们对应离散方程联合地面条件和NLBC 单独推导即可。

4 矩阵预处理与快速求解技术

考察式(5)，其中U 为表征二维场点的M×N 矩阵，A，B，D，E 均为三对角系数方阵。若已知初始场，k+1 平面内的场将通过k 平面的场递推得到。求解这种类型的矩阵方程，传统的做法是先将方程转换成新的矩阵方程Tx=b(这里T 是M×N 阶方阵)，然后运用迭代法。显然，传统做法对计算机的存储量要求很高，求解速度慢，不能适应大范围、远距离电波传播特性预测的要求。为克服这一缺点，本文考虑先将矩阵进行Schur 分解，再实现快速求解。

对于式(5)，令DU+UE=C，则

这种方程也称作Sylvester 方程。矩阵预处理技术如下，先将矩阵A，B 进行Schur 分解:

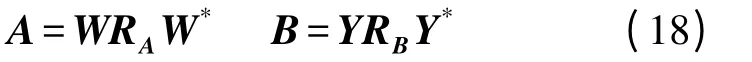
式中W，Y 为酉矩阵，即W*W=WW*=I，Y*Y=YY*=I。RA和RB均为上三角矩阵，其主对角元素分别是矩阵A 和B 的特征值，特征值对应的特征向量分别构成W，Y 的列。

将式(18)代入式(17)，得:WRAW*U+UYRBY*=C，然后在方程两边分别左乘矩阵W*，右乘矩阵Y，同时利用酉矩阵的性质，有:RAW*UY+W*UYRB=W*CY

令W*UY=，W*CY=，于是方程转化为

此时问题转化为已知矩阵^C，求解矩阵^U。显然，式(19)的求解非常简单且快速，只需直接回代，因为矩阵RA和RB均是上三角矩阵。一旦求得^U，则最初的待求矩阵为:

5 算例与讨论

为检验我们的算法，以电波在平静海平面上的传播为例，计算电波传播损耗值。并将结果与双射线法［5］比较。假设发射天线高度为ht=5 m，信号工作频率f=1 GHz，接收天线与发射天线之间水平距离为d=1 000 m，海水电参数为:εr=80，σ=4 S/m。取空间步长为Δx=4λ，Δy=3λ，Δz=2λ，场矩阵U 在z，y 方向上的点数分别为M=120，N=30，大约迭代835 步。

图2、图3 分别展示了CNFD 算法结合NLBC 边界计算垂直极化和水平极化下的电波传播损耗随接收天线高度变化的结果，CNFD 算法与双射线法吻合得很好，但随着接收天线高度的增加，CNFD 结果的出现不稳定但总体上还是比较吻合，验证了算法的正确性。

图2 垂直极化下二种方法的比较

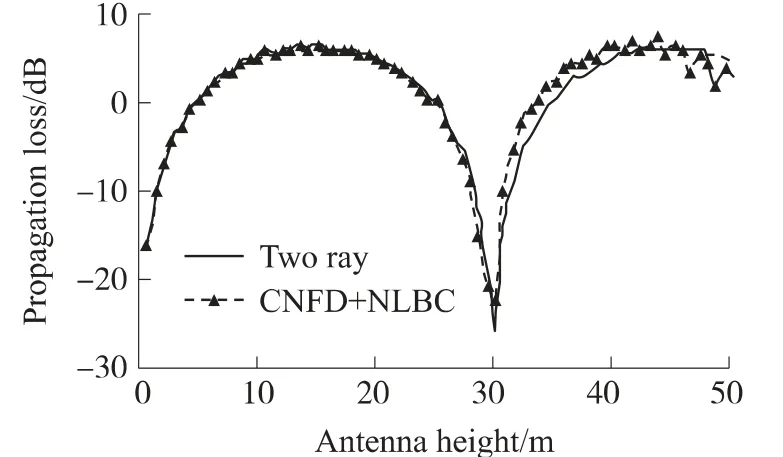
图3 水平极化下二种方法的比较

最后，我们将矩阵预处理技术与传统的迭代法求解技术进行了比较研究，发现:以CPU 主频为2 GHz 的单机为例，同样求解130×30 个场点(其他参数与图2、图3 中的算例完全相同)，采用迭代法需要8 h(收敛精度取10－8)，而借助矩阵预处理技术，只需2 min。显然，矩阵经过预处理后求解速度大大提高。另一方面，先将矩阵进行Schur 分解，还可以大大改善计算机存储量的限制情况。以单机2 G 内存为例，采用迭代法大约可以求解4 000个场点，而采用矩阵预处理技术，可以求解约32 000个场点，提高了整整7 倍，这为预测大尺度宽范围的电波传播特性提供了可能。

6 结论

本文研究了用3DPE 方法预测电波传播的衰减问题，结合CNFD 技术，结果与双射线法结果吻合很好。而且矩阵预处理技术的运用是非常成功的，不但大大改善了计算机存储量的限制状况，同时实现了场值的快速递推，为后续的程序调试和研究工作节省了大量时间。

［1］ Levy M F. Parabolic Equationmethods for Electromagnetic Wave Propagation［M］.London:IEE Press，2000:6－45.

［2］ Zelley C A，Constantinou C C. A Three－Dimensional Parabolic Equation Applied to VHF/UHF Propagation over Irregular Terrain［J］. IEEE Transactions on Antennas ans Propagation，1999，47(10):1586－1596.

［3］ 胡绘斌. 预测复杂环境下电波传播特性的算法研究［D］. 长沙:国防科学技术大学，2006.

［4］ 胡绘斌，柴舜连，毛钧杰. 宽角抛物方程在阻抗边界条件下的应用［J］.电波科学学报，2005，20(4):500－504.

［5］ 胡绘斌，柴舜连，毛钧杰.基于三维PE 方法的雷达波传播损耗估计［J］.微波学报，2005，21(2):4－7.

［6］ Hoffman J D. Numerical Methods for Engineers and Scientists［M］.New York:McGraw－Hill，1992.

［7］ Taflove A，Hagness S C. Computational Electrodynamics:The Finite－Difference Time－Domain Method［M］. 2nd ed. Artech House，Inc.，2000.

［8］ 李永顺.基于抛物线方程求解电大尺寸目标双(多)站RCS 方法的研究［D］.合肥:安徽大学，2005.

［9］ 李方，察豪.抛物线方程法研究不规则地形对电波传播的影响［J］.火力与指挥控制，2010，35(8):114－116.

［10］ 孔勐，吴先良.Pade(1，0)抛物线方程方法求解三维电磁散射问题［J］.安徽大学学报:自然科学学报，2008，32(32):44－47.

［11］ 孔勐，胡玉娟，吴先良.标准抛物线方程SSFT 算法在电波传播问题中的应用［J］.安徽大学学报:自然科学学报，2011，35(3):2－4.

［12］ 唐海川，黄小毛，吴绳正，等.海上大气负折射现象及其对电波传播影响分析［J］.微波学报，2009，25(6):43－48.

［13］ 王文祥.微波工程技术［M］.北京:国防工业出版社，2009.

［14］ 谢益溪.无线电波传播原理与应用［M］. 北京:人民邮电出版社，2008:61－120.

［15］ 熊皓.无线电波传播［M］.北京:电子工业出版社，2000:403－413.