重力对载人航天器密封舱内空气 对流换热影响的数值分析

王 晶 ，徐向华 ，李西园 ，陶 涛 ，裴一飞

（1.可靠性与环境工程技术重点实验室，北京 100094；2.北京卫星环境工程研究所，北京 100094；3.清华大学 航天航空学院，北京 100084）

0 引言

空间站、载人飞船等载人航天器都必须有密封舱以维持正常大气环境供航天员工作、生活。而密封舱由于运行在空间微重力环境中，其内部无法形成自然对流。因此，载人航天器密封舱必须利用风机、风扇等通风设备使空气强迫对流[1]，以带走乘员、设备产生的废热和污染物，并维持舱内适宜的温度、湿度和风速分布。研究密封舱内的通风换热特性对于设计舱内通风系统乃至航天器的环控生保系统都具有重要的意义。

空间微重力环境下密封舱内部的传热、传质情况与地面重力环境下存在很大不同，没有“冷风下坠”或者“热羽流”现象[2]。目前在密封舱内空气传热的相关研究和工程中应用的方法主要有数值模拟和模拟试验。数值模拟主要是通过计算流体动力学（CFD）方法，采用商业流体模拟软件对密封舱内的空气流动速度场和温度场进行数值求解，进而分析其特性。针对方形空间内空气流动传热受浮力和剪切力的影响，Tian 等人[3-4]展开了大量的数值分析研究。数值模拟方法简便、快速、成本低，可以方便地模拟重力和各种边界条件，但其准确性需要 通过试验验证。而模拟试验的难点是消除重力对对流换热的影响。在地面产生微重力环境的常规手段（如落塔、探空火箭、飞机抛物线飞行等）不但费用很高，而且所能够提供的连续的微重力时间较短，难以进行换热试验。因此，目前所采用的消除重力影响的对流换热试验方法主要是基于相似理论的比拟方法，具体又分为缩比法和减压法。缩比法在保证准则数的基础上调整几何和边界条件，以达到削弱自然对流的作用，使得在地面试验中得到与微重力条件下相似的流体流动和传热结果[5-7]。它的缺点是需要建立较小的模型，因而难以操作。减压法则通过降低密封舱内压力、增加流体流速的方式抑制自然对流换热[8-9]，并且可以针对原型舱进行试验，因此实际应用较多[10-11]。减压法一般要求密封舱内压力降低到0.3 个大气压才能够认为已将自然对流抑制到可以忽略的程度，这给试验的进行带来了困难。

近年来随着航天器的大型化，使得在环境模拟器中进行密封舱的热试验越来越少，而在常压环境中进行热试验的需求增长迅速。但是航天器密封舱设计为只能承受正压而不能承受负压，在常压环境中进行热试验无法采用减压方法抑制舱内的自然对流，因此有必要研究在地面常压热试验中重力对舱内空气对流换热的影响，并根据这种影响的特点提出试验方法或者对试验结果的修正方法[12]。

本文以一个简化的航天器密封舱内的空气对流换热为分析对象建立数值模型，并针对几种典型通风工况模拟有无重力时舱内的温度场和换热量的差别，分析重力对舱内空气换热的影响特点。

1 模型的建立与计算设置

1.1 几何模型

本文研究的对象包括一个长方体的密封舱（以下称试验舱）和一个接近立方体的气闸舱，其外形见图1。试验舱长5.5 m，横截面为正方形，边长2 m，有10 对进风口和10 对出风口。进风口位于舱体上方的两个角部，出风口位于舱体下方的两个角部，与侧壁均成45°角。进风口和出风口的尺寸均为宽0.2 m，长0.25 m。气闸舱边长1.5 m，其顶壁有1个进风口。试验舱与气闸舱间支持舱间通风，其通风方式为将一部分从试验舱出风口送出的空气输送到气闸舱的进风口，气流进入气闸舱后再经过气闸舱与试验舱的连接处返回试验舱。

图1 试验舱与气闸舱的结构外形Fig.1 Configuration of the experimental cabin and the airlock cabin

1.2 数学模型

密封舱内空气的流动和传热过程可用Navier- Stokes 方程和能量守恒方程描述，具体满足以下控制方程。

连续性方程：

动量守恒方程：

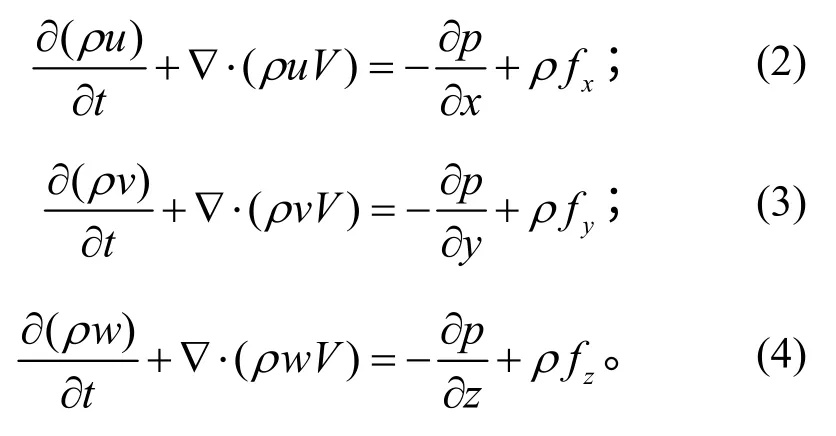
能量守恒方程：

湍流方程（以RNGκ-ε为例）：

1.3 计算域网格划分

本文采用商业CFD 软件FLUENT 6.3.26 来模拟密封舱内的空气流动和传热，所模拟的区域包括图1所示的全部区域。对进风口和出风口分别采用速度入口边界条件和出口边界条件，为了计算的稳定，需要给进口和出口分别增加一段等截面的进口段和出口段，参见图1。

用GAMBIT 软件进行结构化网格划分。进风口处的截面网格见图2，在进出口和边界处进行适当 的加密。经过网格无关性验证，最终采取的网格划分方案为：试验舱横截面上的网格间距为2 cm，进出口加密1 倍，轴向网格间距为5 cm；气闸舱截面的网格数与试验舱相同。网格总节点数为285 万。

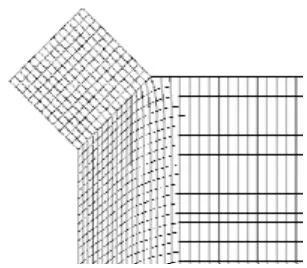
图2 试验舱进风口处的截面网格划分Fig.2 Meshes of the air inlet section of the experimental cabin

1.4 边界条件与计算设置

所采用的求解模型和边界条件设置如下。

1）湍流模型：RNGκ-ε模型，标准壁面函数；

2）空气密度模型：不可压缩理想气体；

3）试验舱进风口：速度入口边界，给定温度；

4）试验舱出风口：出口边界，左右两侧出口流量相等；

5）气闸舱进风口：速度入口边界，温度等于试验舱出风口的平均温度，利用用户自定义函数（UDF）统计得出；

6）试验舱壁面：温度边界，设置为27 ℃；

7）气闸舱壁面：绝热边界。

壁面间还会产生辐射换热，但由于大部分的壁面温度都相等，因此换热量很小。通过数值模拟验证发现，考虑辐射换热与不考虑辐射换热对模拟结果的影响可以忽略，因此在本文数值模拟中不考虑此项。

在FLUENT 中的求解器设置如下。

1）求解器类型：基于压力的隐式稳态求解器。

2）压力-速度耦合方法：SIMPLEC。

3）离散格式：压力在无重力时采用标准格式，有重力时采用PRESTO!格式；动量方程和湍流方程采用二阶迎风格式；能量方程采用QUICK 格式。

4）松弛因子：当压力采用标准离散格式时，各松弛因子均采用默认值；当压力采用PRESTO!离散格式时，压力的松弛因子改为0.7，动量方程的松弛因子改为0.3。

2 模拟结果及分析

为分析不同工况下重力对密封舱内空气对流换热的影响，本文模拟了表1所示的4 种工况。其中，通风流量是指试验舱的总进风流量，转移流量是指从试验舱转移到气闸舱的流量。工况2 中试验舱和气闸舱之间没有通风；工况4 中的通风流量和转移流量均减小一半。

表1 模拟工况参数Table 1 Simulation parameters of four working conditions

4 种工况下、有无重力时，舱内平均温度的模拟结果见表2。由表中数据可见，有重力时自然对流增大了壁面的对流换热量，导致舱内平均温度升高。对比工况1 和工况2 可见，当有舱间通风时，舱内平均温度受重力影响更小。工况3 的进风温度高、与壁面温差小，舱内平均温度受重力影响最小。工况4 的空气流量降低一半，舱内平均温度受重力影响变大。

表2 舱内平均温度的模拟结果对比Table 2 Simulation results of average temperature inside the cabins 单位：℃

4 种工况下、有无重力时，试验舱壁面换热量的模拟结果见表3。由表中数据可知，壁面换热量受重力的影响较大。对于左右壁面，正常通风量（工况1、2、3）时，重力引起的自然对流使得有重力时的换热量比无重力时的增加了约50%；减半通风量（工况4）时，自然对流在空气流量中的占比增加，使得有重力时的换热量比无重力时的增加了约90%。地板的换热量在有重力时也比无重力时的有所增加，但增加量较小，正常通风量时不超过15%，减半通风量时约为21%。顶壁的换热量则是在有重力时小于无重力时，降幅可达30%左右。这是由于在有重力时热空气上浮，试验舱顶部的气温升高，使得顶壁与空气的温差减小，导致换热量减小。

表3 试验舱壁面换热量的模拟结果对比Table 3 Simulation results of heat transfer amount inside the experimental cabin 单位：(W/m2)

为比较各工况下舱内空气温度受重力影响的分布，将试验舱和气闸舱均沿轴向按0.5 m 的间隔划分为若干区域，每块区域又按对称线划分为4 个象限单元。试验舱有12 个轴向区域，48 个单元；气闸舱有4 个轴向区域，16 个单元。4 种工况下各区域空气温度受重力影响沿主轴（z轴）的分布见图3。图中，z=0～16 表示由图1所示气闸舱前端部至试验舱后端部依次排列的16 个轴向区域。 图3各分图中的上图表示各区域上部的2 个象限单元的温差（有重力时与无重力时的单元平均温度之差），下图表示各区域下部的2 个象限单元的温差。

图3 重力对舱内各区域温度影响的分布Fig.3 Influence of gravity on the local temperature inside the cabins

由图3可见，各工况下平均温度受重力影响在舱内各区域分布比较均匀，上部和下部也没有明显的差别。工况1 中试验舱受重力影响的温差大部分都在1 ℃以下，气闸舱的则在0.5 ℃以下。这是因为气闸舱内的气流速度高，受迫对流换热强，自然对流在空气流量中的占比小。当没有舱间通风（工况2）时，试验舱的温差有所增加，而气闸舱内的温差更是增大了2 倍以上，超过了试验舱。工况3的进风温度高、与壁面的温差减小，自然对流的影响也相应减弱，因此重力对单元温度的影响也大幅度降低。当通风量减半（工况4）时，受迫对流换热强度下降，自然对流在空气流量中的占比增大，因此重力对空气温度的影响相应增大，试验舱内单元平均温度有无重力时的温差达到1.5 ℃，气闸舱的也超过了1 ℃。

重力使得热空气上浮、冷空气下沉；但由于舱内通风的方向为上进下出，与自然对流的方向相反，因此会减弱空气的上下分层现象。图4是工 况1 中竖直中心截面的温度分布，可见温度的上下分层不明显，但在有重力时贴近顶壁有一薄层热空气聚集，正是这层热空气使得顶壁的换热量在重力影响下有所减小。

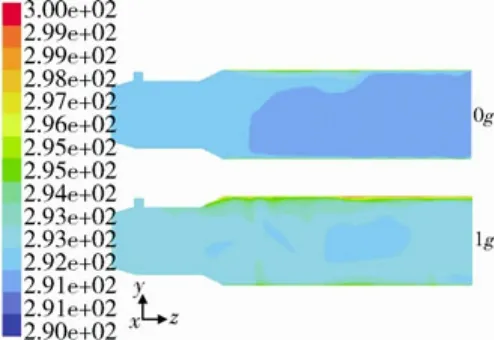
图4 有无重力时竖直中心截面的温度分布云图Fig.4 Temperature distribution on the central section with and without gravity

分析模拟结果发现，重力的影响主要表现在密封舱侧壁面换热量的增加，同时舱内的流场也发生了变化。有重力时，在两个侧壁附近产生了上升流动，因而在侧壁附近形成了涡流，总体上增强了空气的流动，扰乱了流场，使流场的不对称性增加。

3 结论

本文通过对简化的航天器密封舱内通风换热进行建模和数值模拟，分析了重力对壁面换热量、区域平均温度分布及舱内流场的影响，得到如下主要结论：

1）重力对壁面换热量的影响较大。有重力时，自然对流增加了侧壁和地板的换热量，而顶壁的换热量减小。有无重力的换热量差别随着进风口与壁面间温差的减小而减小，随空气流量的减小而增大。

2）有重力时增加的壁面换热量使得舱内平均温度升高，但在所研究参数范围内的升高幅度小于1.5 ℃。重力对区域温度影响的空间分布比较均匀。舱间通风能够减弱重力对舱内空气温度的影响。有无重力时的舱内空气温度差随进风口与壁面间温差的减小而减小，随空气流量的减小而增大。

3）在地面常压、重力环境中进行密封舱内通风换热试验时，重点需要对壁面换热量进行修正。在此前提下，舱内空气温度分布可认为与微重力条件下差别不大。

（References）

[1]卢威, 黄家荣, 范宇峰, 等.载人航天器密封舱流动和传热数值模型及其地面验证[J].宇航学报, 2011, 32(5)∶959-965 Lu Wei, Huang Jiarong, Fan Yufeng, et al.Numericalmodel of flow and heat transfer for manned spacecraft pressurized cabin and its ground verification[J].Journal of Astronautics, 2011, 32(5)∶959-965

[2]郑忠海, 张吉礼.载人航天器舱内通风空调特性和数值模拟[J].建筑热能通风空调, 2005, 24(8)∶86-90 Zheng Zhonghai, Zhang Jili.Numerical simulation and characteristic of manned spacecraft ventilation and air conditioning[J].Building Energy &Environment, 2005, 24(8)∶86-90

[3]Tian Y S, Karayiannis T G.Low turbulence natural convection in an air filled square cavity∶(part I) The thermal and fluid flow fields[J].International Journal of Heat and Mass Transfer, 2000, 43∶849-866

[4]Tian Y S, Karayiannis T G.Low turbulence natural convection in an air filled square cavity∶(part II) The turbulence quantities[J].International Journal of Heat and Mass Transfer, 2000, 43∶867-884

[5]Liang Xin’gang, Guo Zengyuan, LiuYunlong, et al.Ground simulation of the flow and heat transfer under microgravity[J].Science China (Series A), 1997, 27 (11)∶1009-1013

[6]任建勋, 姬朝玥, 梁新刚, 等.微重力条件下舱内对流换热的地面质-热比拟[J].工程热物理学报, 2001, 22(6)∶717-720 Ren Jianxun, Ji Chaoyue, Liang Xin’gang, et al.Ground-based mass-heat analogy of convection in cabins in micro-gravity[J].Journal of Engineering Thermophysics, 2001, 22(6)∶717-720

[7]李劲东.航天器密封舱微重力对流传热与传质地面试验模拟方法理论分析[J].宇航学报, 2004, 25(4)∶355- 359 Li Jindong.Theoretical analysis of ground testing simulation of heat and mass convection under micro- gravity for spacecraft[J].Journal of Astronautics, 2004, 25(4)∶355-359

[8]张学学, 刘静, 蒙毅.载人飞船座舱内空气对流换热地面模拟[J].清华大学学报∶自然科学版, 1999, 39(6)∶67-70 Zhang Xuexue, Liu Jing, Meng Yi.Ground-test simulating of air heat convection in manned space capsule[J].Journal of Tsinghua University∶Science and Technology, 1999, 39(6)∶67-70

[9]姬朝玥, 任建勋, 梁新刚, 等.微重力下对流换热的地面缩比-减压模拟技术[J].清华大学学报∶自然科学版, 2001, 41(2)∶92-94;98 Ji Chaoyue, Ren Jianxun, Liang Xin’gang, et al.Ground-based scale and pressure reduction technology for simulation of convection in micro-gravity[J].Journal of Tsinghua University∶Science and Technology, 2001, 41(2)∶92-94;98

[10]黄家荣.载人飞船热平衡试验运用降压法抑制自然对流的影响[J].航天器环境工程, 2004, 21(1)∶37-43 Huang Jiarong.The suppression of natural convection using pressure-reducing method in vacuum thermal balance test of manned spacecraft[J].Spacecraft Environment Engineering, 2004, 21(1)∶37-43

[11]付仕明, 潘增富.载人航天器舱内气压下降时的空气强制对流换热[J].中国空间科学技术, 2007, 27(4)∶44-47 Fu Shiming, Pan Zengfu.Heat transfer of air forced convection with dropping atmosphere pressure in manned spacecraft cabin[J].Chinese Space Science and Technology, 2007, 27(4)∶44-47

[12]张吉礼, 梁珍, 郑忠海, 等.载人航天空间站舱内通风对流换热数值研究进展[J].暖通空调, 2006, 36(1)∶28-34 Zhang Jili, Liang Zhen, Zheng Zhonghai, et al.Numerical simulation progresses of convection heat transfer in manned space craft cabin[J].Heat Ventilating and Air Conditioning, 2006, 36(1)∶28-34