航天器总装精度测量中一种不规则棱镜 矢量计算方法

王 伟，刘 笑，郭洁瑛，孙 刚，刘浩淼

（北京卫星环境工程研究所，北京 100094）

0 引言

航天器总装精度测量一般是通过被测设备上安装的立方镜来实现的。所使用的立方镜是标准的立方体结构，通过对立方镜相邻平面的测量可以得到两个相互垂直平面的矢量，再利用矢量叉乘计算则可获得与这两个平面都垂直的另一平面的矢量。但在实际测量中，有时会受到被测设备在航天器上安装位置的限制，导致精度测量光路被遮挡而无法采用立方镜，为此，需要采用不规则棱镜来替代。

由于在某型号的总装精度测量中出现了测量光路被遮挡的问题而无法使用常规的立方镜，故采用切角为135º 的不规则棱镜，即被切角的斜面与某个直角平面的夹角为135º，这样就避开了遮挡。这种不规则棱镜在航天器的总装精度测量中首次采用。

但是在精度测量中，不能利用立方镜的测量计算方法来得到切角为135º 的不规则棱镜三个相互垂直平面的法线与航天器坐标系所成的角度。针对这种特殊情况，本文首次提出了切角为135º 的不规则棱镜三个相互垂直平面的法线与航天器坐标系所成矢量的计算方法，解决了航天器总装精度测量中出现的难题。

1 航天器总装精度测量原理

航天器总装精度测量的目的就是使用由多台经纬仪构成的非接触式大尺寸测量系统，测量出有精度要求的设备在航天器坐标系下的角度和位置度，并将其调整到位。

航天器总装精度测量的目标是标准的立方镜。即在航天器上合适的位置安装一块基准立方镜，它的三个相互垂直平面的法线和立方镜中心点所构成的坐标系就代表了航天器坐标系（它们之间的关系是固定的）。同样，在有精度要求的设备上都安装了一块立方镜，其三个相互垂直平面的法线和立方镜中心点所构成的坐标系即为设备的坐标系。

在进行航天器总装精度测量时，使用经纬仪测量系统布站定标可以测得设备立方镜中心点在基准立方镜坐标系下的位置度，使用经纬仪测量系统布站准直和互瞄可以测得设备立方镜平面法线在基准立方镜坐标系下的角度；然后再利用基准立方镜坐标系与航天器坐标系之间的关系，就可以计算出被测设备立方镜即设备坐标系在航天器坐标系下的角度和位置度。

进行航天器总装精度测量时，首先要建立基准立方镜坐标系Oj-m1k1n1与航天器坐标系O1-x1y1z1之间的关系。图1为航天器总装精度测量坐标转换示意图。

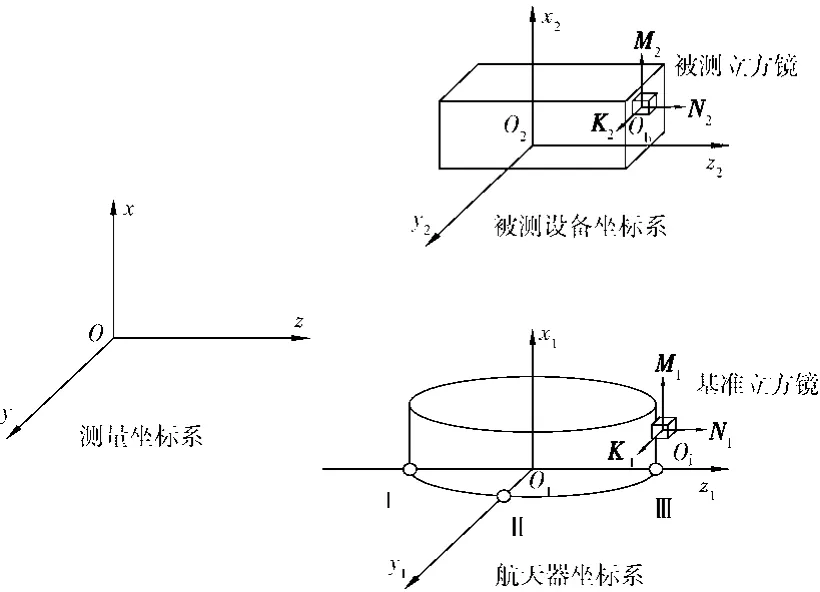
图1 航天器总装精度测量坐标转换示意图Fig.1 Coordinate transformation in the spacecraft integration precision measurement

设通过经纬仪测量系统布站测量并计算可以得到基准立方镜中心点Oj在航天器坐标系O1-x1y1z1下的坐标为而基准立方镜相互垂直平面的三条法线在坐标系O1-x1y1z1下的矢量M1、K1、N1分别为则可得到基准立方镜坐标系Oj-m1k1n1到航天器坐 标系O1-x1y1z1的旋转矩阵和偏移量，即

再建立被测设备上立方镜坐标系Ob-m2k2n2与基准立方镜坐标系Oj-m1k1n1的关系。设由经纬仪布站测得设备上立方镜中心点Ob和及其平面法线矢量K2相对于基准立方镜坐标系Oj-m1k1n1的偏移量Obj和矢量Kk2j分别为则其在航天器坐标系O1-x1y1z1下的偏移量和矢量可以由 旋转平移得到：

同理可以求出被测设备立方镜法线N2在航天器坐标系下的矢量。

2 切角为135º不规则棱镜矢量的计算方法

近来在某型号的设备精测中采用了一种切角为135º 不规则棱镜，即不规则棱镜的坐标系就代表了该设备的坐标系（如图2所示）。

图2 切角为135º不规则棱镜结构示意图Fig.2 The structure of 135-degree-angle irregular prism

根据该设备在航天器上安装极性的要求，需要给出切角为135º 不规则棱镜的三个相互垂直平面A、C及D的法线与航天器坐标系三个坐标轴所成的角度。但受该设备在星体上安装位置的限制，使用经纬仪和现有的精度测量软件只能准直测量得到平面A和斜面B的法线在航天器坐标系下的角度，而无法直接测得三个直角平面法线在航天器坐标系下的角度。因而需要给出其三个相互垂直的平面法线在航天器坐标系下矢量的计算方法。

首先，计算出直角平面C的法线在航天器坐标系下的矢量M3。通过经纬仪测量系统可以得到直角平面A和斜面B的法线在航天器坐标系O1-x1y1z1下的矢量分别为则平面C的法线在航天 器坐标系O1-x1y1z1下的矢量为

将矢量N3和I的值代入式(5)，可得

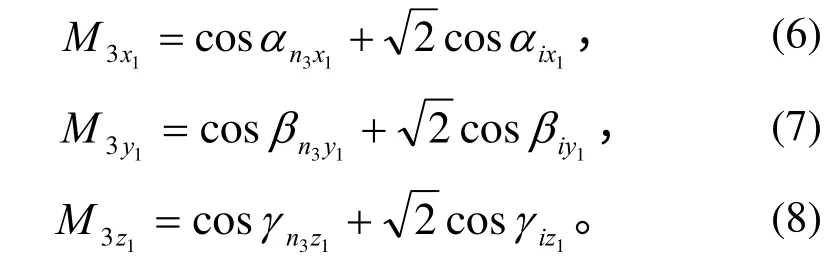
分别对式(6)、(7)、(8)进行归一化处理，就可以得到直角平面C的法线在航天器坐标系O1-x1y1z1下矢量M3的最终结果为

这样就知道了切角为135º 不规则棱镜两个相互垂直直角平面A和C的法线在航天器坐标系O1-x1y1z1下的矢量N3和M3。

然后，再计算出垂直于平面A和C的第三个直角平面D的法线在航天器坐标系O1-x1y1z1下的矢量

K3等于M3与N3两个矢量的叉乘[3]并符合右手法则，即

将矢量N3的值和式(9)～式(11)代入式(12)中，可得

分别对式(13)、(14)、(15)进行归一化处理，就可以得到平面D的法线在航天器坐标系O1-x1y1z1下矢量K3的最终结果为

经过以上计算，最终可以得到平面A、C和D的法线在航天器坐标系下的矢量矩阵 1yA为

对式(19)进行反余弦计算即可得到平面A、C及D的法线在航天器坐标系下的角度分别为

至此我们就得到了切角为135º 不规则棱镜的三个相互垂直平面的法线在航天器坐标系下的角度，依据该被测镜在航天器坐标系下角度的设计值和精度要求将其调整到合格范围内，从而也就完成了使用切角为135º 不规则棱镜为被测目标镜的设备的精度测量工作。

3 计算实例

某航天器设备的精度测量采用了切角为135º的不规则棱镜作为目标镜，通过经纬仪测量系统可以得到该棱镜直角平面A和斜面B的法线在航天器坐标系下的矢量分别为N3(-1.745 33e-5, -4.188 79e-5, 0.999 999 999 0)与I(9.250 25e-5, 0.707 157 379 0, 0.707 056 180 0)。使用本文的计算方法，得到了该棱镜直角平面C和D的法线在航天器坐标系下的矢量分别为M3(1.133 620e-4, 0.999 999 991 0, 7.155 78e-5)、K3(0.999 999 993 0, -1.133 630e-4, 1.7448 6e-5)。再对三个矢量分别进行反余弦计算，则可以得到该棱镜的三个相互垂直的平面A、C及D的法线在航天器坐标系下的角度分别为(90.001 0°, 90.002 4°, 0.002 6°)、(89.993 5°, 0.007 7°, 89.995 9°)和(0.006 8°, 90.006 5°, 89.999 0°)。计算结果得到了验证和认可。

目前该精测设备在轨运行良好，进一步证明了此计算方法的正确性。

4 结束语

本文提出了一种切角为135º 不规则棱镜的三个相互垂直的直角平面法线在航天器坐标系下矢量的计算方法，并对其进行了实例验证。该计算方法解决了航天器总装精度测量中因使用标准立方镜以致遮挡光路而无法进行精度测量的难题，得到了各方的一致认可并已经应用到后续型号的精度测量中，取得了良好的效果。另外，本文只介绍了切角为135°不规则棱镜矢量的计算方法，其他切角度值不规则棱镜的矢量也可采用本文的思路进行计算。

（References）

[1]杨再华.航天器总装精度测量方法分析[J].航天器环 境工程, 2007, 24(6):390-391 Yang Zaihua.An analysis of measurement technology in spacecraft assembly[J].Spacecraft Environment Engineering, 2007, 24(6):390-391

[2]任春珍, 杨再华, 孙刚, 等.太空环境飞行器交会对接设备精测工艺方法研究[J].航天器环境工程, 2010, 27(6):768-769 Ren Chunzhen, Yang Zaihua, Sun Gang, et al.Ground- based alignment of rendezvous and docking device used for objective space vehicle[J].Spacecraft Environment Engineering, 2010, 27(6):768-769

[3]蒋大为.空间解析几何及其应用[M].北京:科学出版社, 2004:31-35