Study of TSP based on self-organizing map

SONG Jin-juan (宋锦娟)， BAI Yan-ping (白艳萍)， HU Hong-ping (胡红萍)

(Department of Mathematics, North University of China, Taiyuan 030051, China)

Study of TSP based on self-organizing map

SONG Jin-juan (宋锦娟)， BAI Yan-ping (白艳萍)， HU Hong-ping (胡红萍)

(Department of Mathematics, North University of China, Taiyuan 030051, China)

Self-organizing map (SOM) proposed by Kohonen has obtained certain achievements in solving the traveling salesman problem (TSP). To improve Kohonen SOM, an effective initialization and parameter modification method is discussed to obtain a faster convergence rate and better solution. Therefore, a new improved self-organizing map (ISOM) algorithm is introduced and applied to four traveling salesman problem instances for experimental simulation, and then the result of ISOM is compared with those of four SOM algorithms: AVL, KL, KG and MSTSP. Using ISOM, the average error of four traveling salesman problem instances is only 2.895 0%, which is greatly better than the other four algorithms: 8.51% (AVL), 6.147 5% (KL), 6.555% (KG) and 3.420 9% (MSTSP). Finally, ISOM is applied to two practical problems: the Chinese 100 cities-TSP and 102 counties-TSP in Shanxi Province, and the two optimal touring routes are provided to the tourists.

self-organizing maps (SOM); traveling salesman problem (TSP); neural network

CLD number： O221.1 Document code： A

Traveling salesman problem (TSP), as a classical combination optimization problem, can be defined as a given graph G=(V; A), where V is a set of n vertices and A is a set of arcs between vertices, and each arc is associated with a nonnegative distance. TSP is to determine a minimum distance of the closed ring passing through each vertex once and only once[1,2]. As a typical NP-complete problem, TSP has vast practical applications in our life, such as vehicle routing[1], power-distribution network[3]and printed-circuit-board manufacturing[4,5]and so on, therefore, it has attracted great research attention.

In recent years, some heuristic intelligent algorithms have been developed and applied to TSP in order to achieve a near-to-optimal solution of the problem in a relatively short period of time. Using heuristic algorithms, such as exhaustive search method, tabu search algorithm (TSA)[6], simulated annealing (SA)[7], genetic algorithm[8], ant colony system[9]and neural networks, etc., TSP is easier to be solved successfully. Self-organizing map (SOM) neural network[10,11], as a kind of Kohonen-type network, has also been used to solve TSP. So in this paper, firstly, we explain SOM modification procedure for TSP, then we introduce two parameter modification formulae and initialization methods of SOM put forword by Kohonen, and finally, we analyze the defects of basic SOM and put forword an improved SOM (ISOM) algorithm.

1 SOM modification procedure for TSP

SOM put forword by Kohonen belongs to a special class of neural networks, where each neuron competes with the others to get activated. In order to provide the readers a intuitive and specific description of SOM network procedure for TSP, this paper utilizes the following figure (Fig.1) to explain the association between learning network[12]and a geometrical representation of TSP solution.

Fig.1 Schematic diagram of two-layer neural network and associated geometrical representation

In Fig.1, [ci1,ci2] repesents the coordinates of city cias an input vector, and weights vj1and vj2can be defined as the coordinates of node vjlocated in the output layer. The network is initialized with small random connection weights and then cities are sequentially added to the network in a random order. The nodes in the output layer compete with each other for a given city based on Euclidian distance and then the winner node J is selected by

where xiand yjdenote the coordinates of city i and output node j, respectively, and ‖·‖2is Euclidian distance. From the above formula, we can summarize that the winner node is the node with the minimum Euclidian distance to the existing city.

Once the winner node for a given city is found, the weight vectors of the winner node and its neighbouring nodes are modified in order to get closer to this city according to the following formula:

where f(σ,d)=exp(-d2/σ2) is a neighborhood function: α and σ are learning rate and neighborhood function variance, respectively; d=min{‖j-J‖,M-‖j-J‖} is the cardinal distance measured along the closed ring between nodes j and J, where ‖·‖ represents absolute value and M is the number of the output nodes.

When the network is stable, each city can find its corresponding winner node. Furthermore, all the winner nodes form a closed ring, and after modified, the closed ring represents a touring route covering the selected cities and it is approximately optimal solution to TSP.

2 Improvement on Kohonen SOM

In SOM network, there are two adaptive parameters: learning rate α and neighborhood function variance σ, which are vital to solving TSP especially in routing length and processing time to achieve a reasonable and optimal solution.

2.1 Parameter modification of ISOM

The new parameter modification formulae proposed in this paper are presented as

where k=0,1,2,…, is the number of iterations, T is a contant related to time, and we give the following initial values: kmax=200, T=10 000 and σ0=10. The modification of learing rate α and neighborhood function variance σ are illustrated in Fig.2 and Fig.3, respectively.

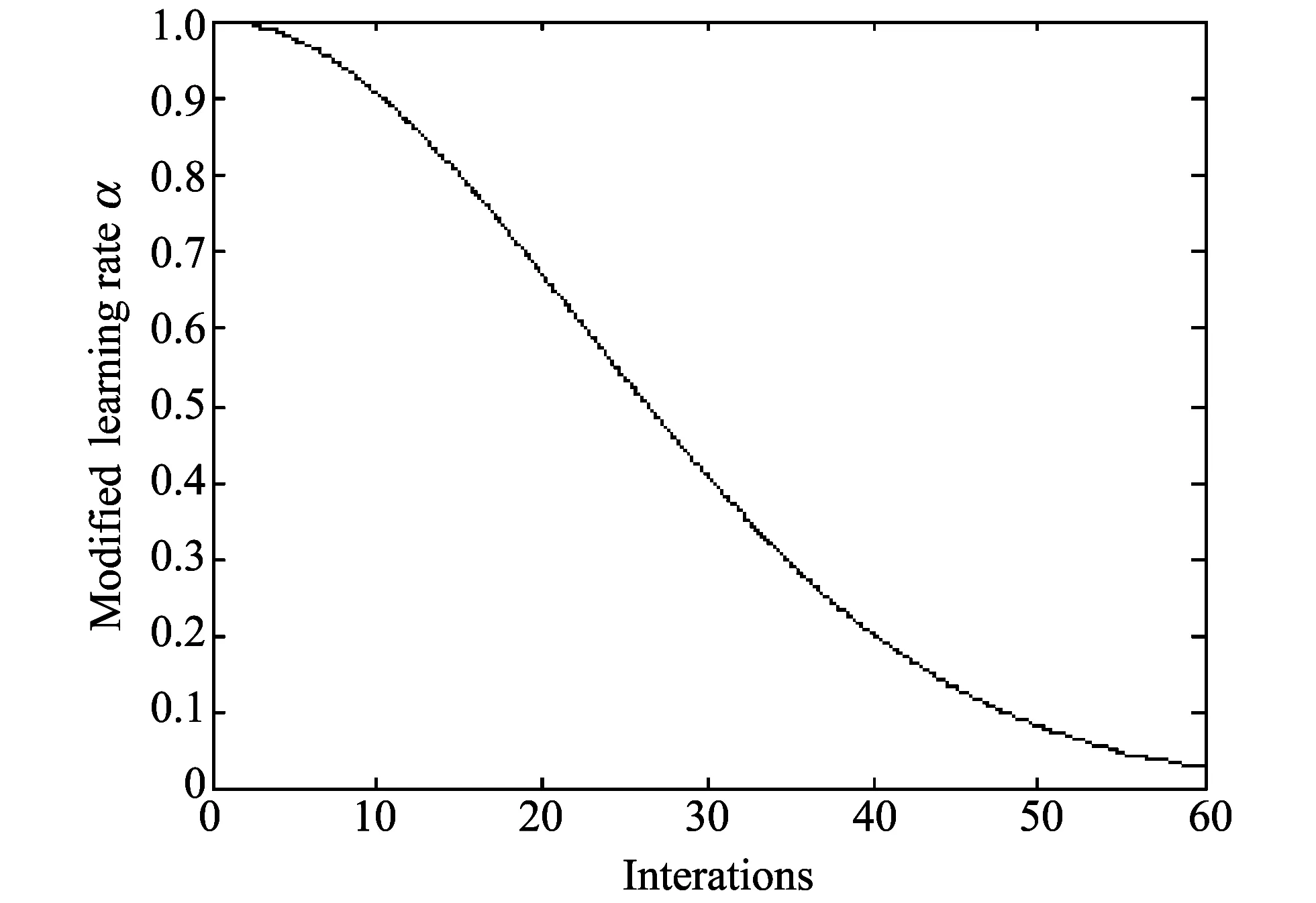
Fig.2 Modified α in ISOM

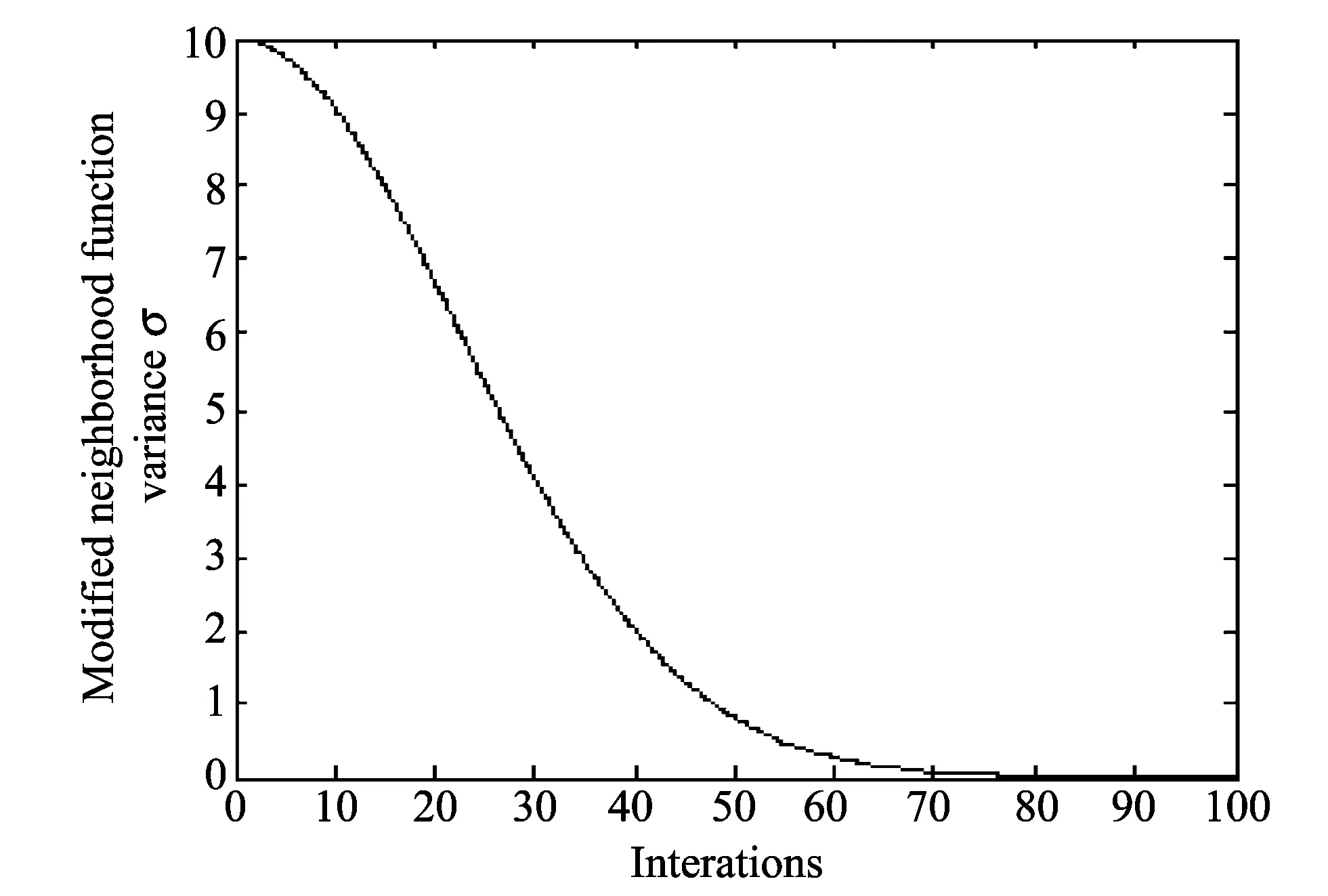
Fig.3 Modified σ in ISOM

2.2 Initialization method of ISOM

Firstly, we suggest that the number of selected output nodes be twice the number of cities (M=2n), and in the initialization stage, the neighbor length be limited to 40% of the output nodes (l=0.4M). Once a cycle is completed (that is when all n cities complete their inputs to the network), the neighboring length will decrease by 2%, which leads to a lower processing efficiency. Secondly, in order to prevent a node from being selected as the winner node for more than one city in each completed cycle of iterations, an inhibitory index is defined for each node, which puts the winner node aside from the competed, providing more opportunities for other nodes. And before each iteration, the sequence of n cities is always permutated randomly. Finally, it is suggested that the nodes initialization be on a rectangular frame located on the right of the n cities' centroid.

3 Experimental results

In order to verify the validity of ISOM algorithm, four examples obtained from general TSPLIB[13]are selected for experiments. Through experimental simulation, the improved algorithm are compared with Kohonen SOM. For each example, the experiment is conducted for 10 times, and then the best value, average value and relative error are calculated, respectively. The experimental results are shown in Table 1.

Table 1 Experimental results' comparison of average values and relative errors of Kohonen SOM and ISOM

The comparison of experimental results above shows that the average values obtained from the improved algorithm are greatly better, and the relative errors are much smaller than that of Kohonen SOM, so the improved algorithm introduced in this paper is an effective algorithm.

The following Figs.4-7 are four experimental results with ISOM.

Fig．4 Optimalroutinggraphofeil76Fig．5 OptimalroutinggraphofKroA200

Fig．6 Optimalroutinggraphofrat195Fig．7 Optimalroutinggraphofpr136

In order to further evaluate and verify the performance of ISOM, it is compared with other four basic heuristic methods, which are AVL (the procedure of Ange_niol, Vaubois and Le Texier[14]), KL-e global-KG[15]and MSTSP (modified SOM applied to the TSP[16]). The comparison results are shown in Table 2.

It can be seen from Table 2 that, for each example of TSP, the experimental results of ISOM are greatly better than those of the other four algorithms. The average errors of four traveling salesman problem instances for five algorithms are: 8.51% (AVL), 6.147 5% (KL), 6.555 0% (KG), 3.420 9% (MSTSP) and 2.895 0% (ISOM), respectively.

In order to deeply understand the convergence process in searching optimal solution, this paper takes st70 from TSPLIB as instance for conducting the experiments, and five figures are shown in the following: the initial condition of M nodes (Fig.8), intermediate iterations (Fig.9, Fig.10 and Fig.11) and final result (Fig.12), where “*” and “·” represent the cities and nodes located in output layer, respectively.

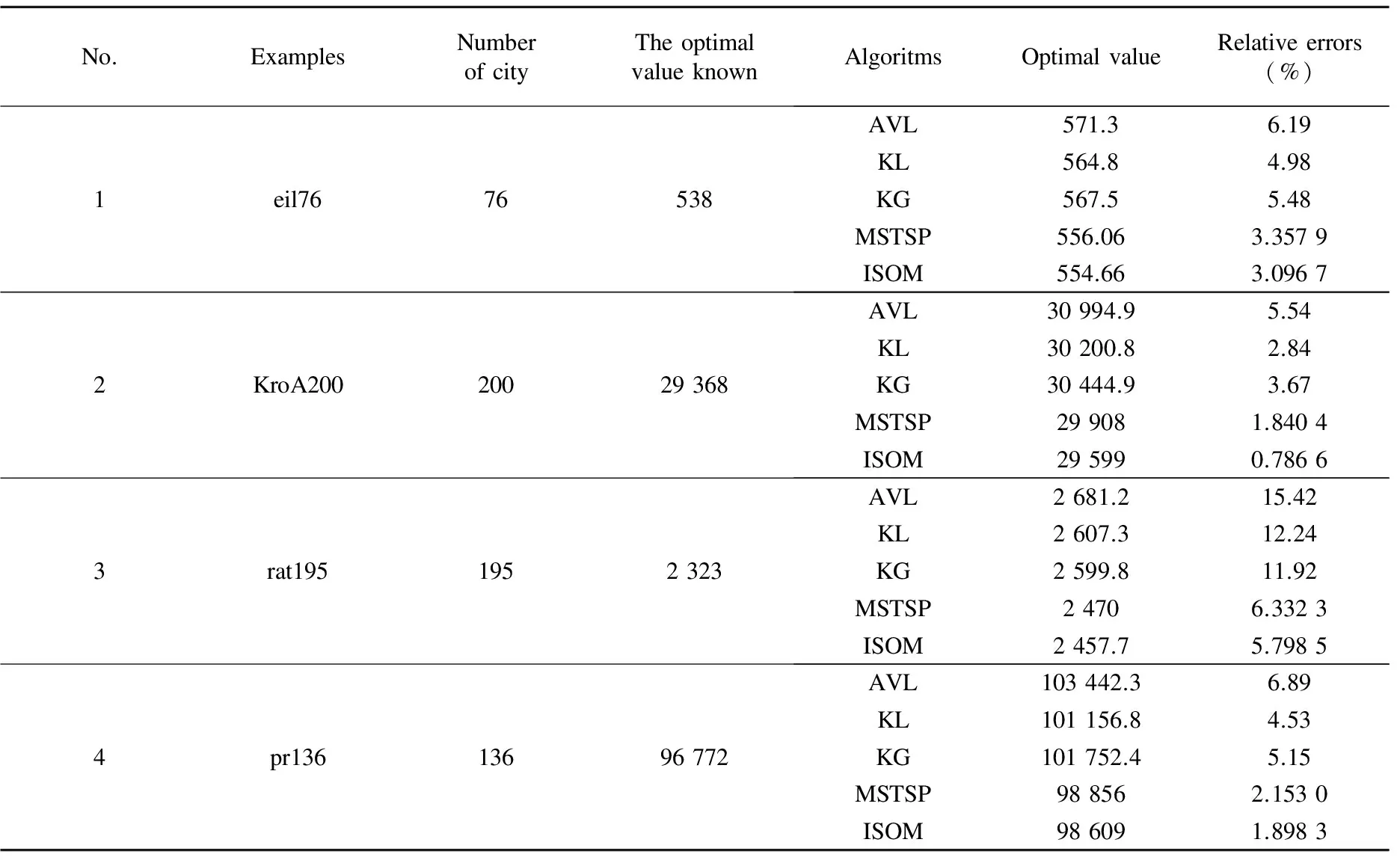
Table 2 Comparison results of five algorithms

Fig．8 InitialconditionofMnodesFig．9 Convergencein50th

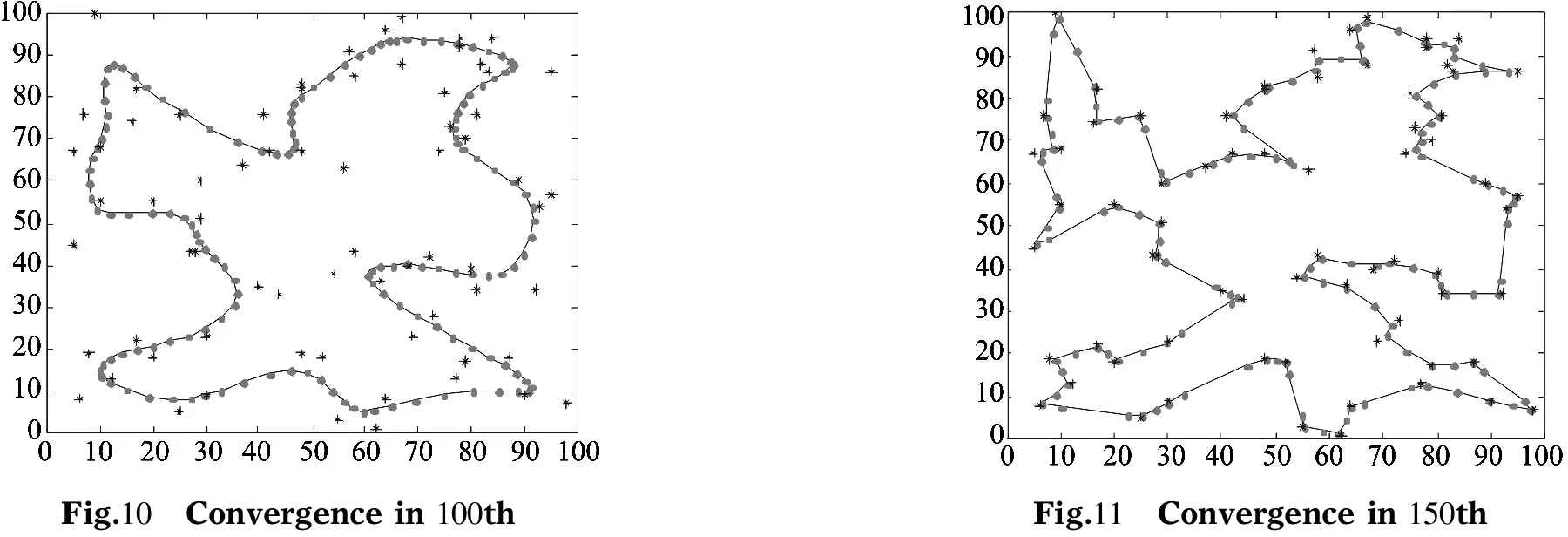
Fig．10 Convergencein100thFig．11 Convergencein150th

Furthermore, Chinese 100 cities-TSP and 102 counties-TSP in Shanxi Province are selected as instances for conducting the experiments. Table 4 and 5 show the names of chinese 100 cities and the coordinates[17]of 102 counties in Shanxi Province, respectively.

The experimental results will provide the tourists with two greatly optimized paths for their traveling in China and even in Shanxi Province.

Firstly, for Chinese 100 cities-TSP, the results obtained by the proposed ISOM are compared with those of other five kinds of SOM algorithms: SKH[17], CGHNN[18], F-W[19], NCSOM[19]and ASOM[19]. The comparison results are shown in Table 3.

Then, for the above two practical instances: the chinese 100 cities-TSP and 102 counties-TSP in Shanxi Province, the results obtained by proposed ISOM algorithm are compared with that of ant colony system (ACS) not only in optimal pathing values but also in time, which is shown in Table 6.

Fig.12 Final result

Table 3 Comparison results of SKH, CGHNN, F-W, nCSOM, ASOM and ISOM

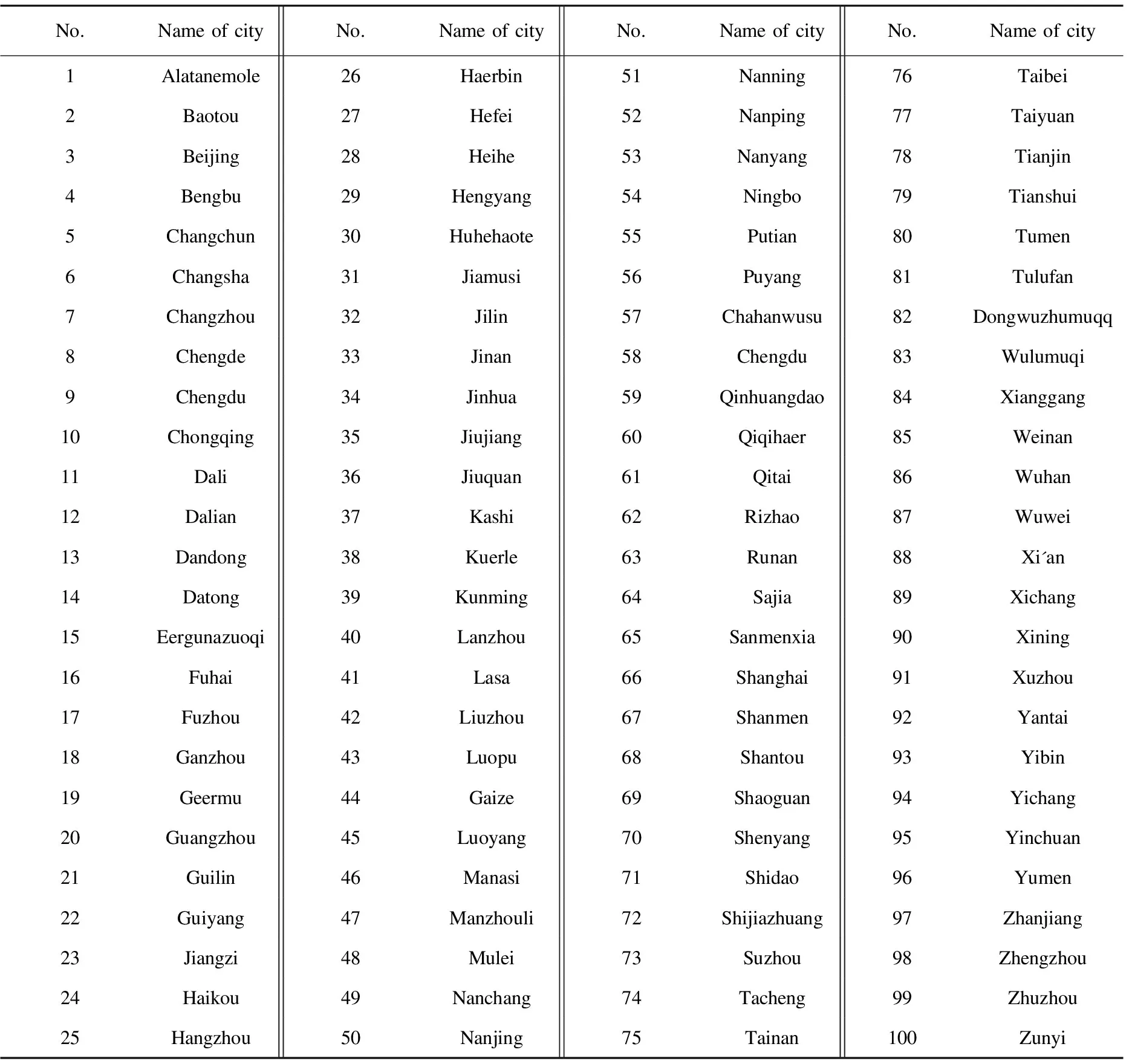
Table 4 Names of Chinese 100 cities

Table 5 Coordinates of 102 counties in Shanxi Province

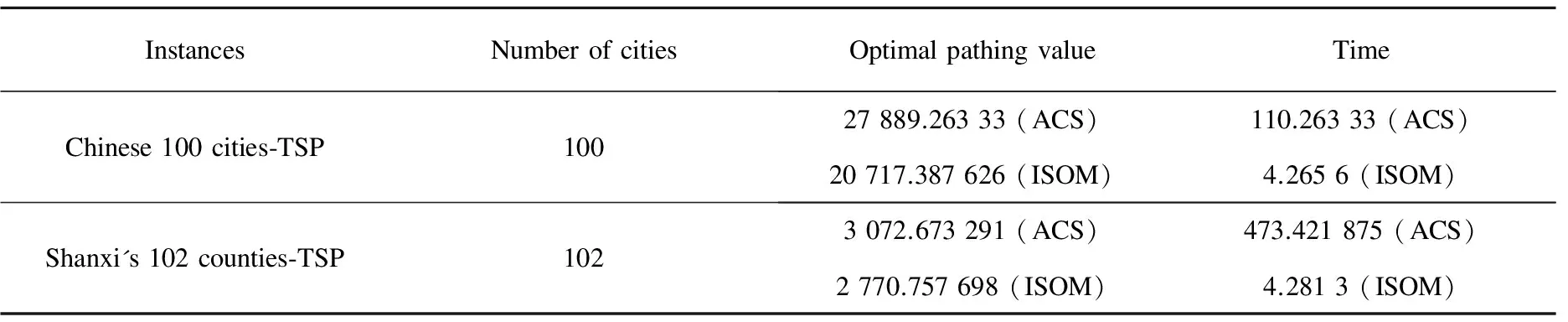
Table 6 Comparison results of ISOM and ACS

From Figs.13 and 14 it can be easily found that the proposed ISOM algorithm provides the tourists with a very optimal path for their traveling in China all follows:

46—38—83—81—61—48—19—57—96—36—90—87—40—95—79—88—85—65—45—98—63—56—72—77—14—30—2—82—1—47—15—60—28—31—80—26—32—5—70—13—71—92—12—59—8—3—78—33—75—62—91—4—27—50—53—7—73—66—54—25—34—67—76—17—55—52—49—35—86—94—6—99—29—69—18—68—84—20—24—97—51—42—21—22—100—10—93—9—89—39—11—58—41—23—64—44—43—37—74—16.

An optimal path in Shanxi Province is:

58—59—60—50—51—52—54—61—83—87—84—86—85—96—100—99—95—94—90—98—4—68—97—93—71—72—73—70—69—67—34—37—12—35—36—38—9—6—13—7—8—10—11—66—64—65—74—62—63—44—16—14—15—43—42—41—22—21—28—19—20—24—17—18—32—23—33—29—30—31—81—27—26—25—40—45—39—3—1—5—2—92—46—47—91—102—101—49—48—88—79—80—82—75—77—78—76—55—53—56—57—89.

Fig.13 Optimal routing graph of Chinese 100 cities-TSP

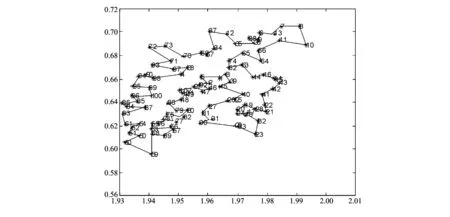
Fig.14 Optimal routing graph of Shanxi's 102 counties-TSP

The experimental results indicate that the proposed ISOM not only provides two convenient traveling routes for the tourists, but also saves them a lot of money, manpower, material resources and time. Therefore, the proposed ISOM algorithm has certain theoretical value and practical significance.

4 Discussion and conclusion

This paper proposes a new kind of ISOM based on Kohonen SOM. From the experimental results above it can be easily found that the neighborhood modification procedure of SOM to TSP becomes more reasonable and effective by improving learning rate and neighborhood function variance, which leads to an optimal solution of TSP. However, the proposed ISOM is only applied to Euclidean TSP, and it will be an interesting research topic whether it can solve non-Euclidean TSP[20].

The combination of SOM network and other heuristic intelligent algorithms such as genetic algorithm (GA), SA, TSA and ACS will be described in solving TSP.

[1] Laporte G. The vehicle routing problem: an overview of exact and approximate algorithms. European Journal of Operational Research, 1992，59 (3): 345-358.

[2] Leung K S, JIN Hui-dong, XU Zong-ben. An expanding self-organizing neural network for the traveling salesman problem. Neurocomputing, 2004, 62: 267-292

[3] Onoyama T, Maekawa T, Kubota S, et al. Intelligent evolutional algorithm for distribution network optimization. In: Proceedings of IEEE International Conference on Control and Applications, 2002, 2: 802-807.

[4] Takashi S, Kenji M, Fujimura K, et al. Optimization of surface component mounting on the printed circuit board using SOM-TSP method. IEIC Technical Report, 1999, 98(673): 289-296.

[5] Fujimura K, Fujiwaki S, Kwaw O C, et al. Optimization of electronic chip-mounting machine using SOM-TSP method with 5 dimensional data. In: Proceedings of International Conference on Info-tech and Info-net, Beijing, China, 2001, 4: 26-31.

[6] Fiechter L. A parallel tabu search algorithm for large traveling salesman problem. Discrete Applied Mathematics, 1994, 51 (3): 243-267.

[7] Van Laarhoven P J M, Aarts E H L. Simulated annealing: theory and applications. Kluwer Academic Publishers, Norwell, USA, 1987.

[8] Goldberg D E. Genetic algorithms in search, optimization and machine learning. Addison-Wesley Publisher, Boston, USA, 1989.

[9] Dorigo M, Gambardella L M. Ant colony system: a cooperative learning approach to the traveling salesman problem. IEEE Transactions on Evolutionary Computation, 1997, 1 (1): 53-66.

[10] Creput J C, Koukam A. A memetic neural network for the Euclidean traveling salesman problem. Neurocomputing, 2009, 72(4-6): 1250-1264.

[11] Kohonen T. The self-organizing map. In: Proceedings of IEEE, 1990, 78 (9): 1464-1480.

[12] Somhom S, Modares A, Enkawa T. A self-organising model for the travelling salesman problem. Journal of the Operational Research Society, 1997, 48 (9): 919-928.

[13] TPSLIB. [2013-01-08]. http://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/.

[14] Angeniol B, la Croxi Vaubois C, Le Texier J Y. Self-organizing feature maps and the traveling salesman problem. Neural Networks, 1988, 1(4): 289-293.

[15] Aras N, Oommen B J, Altinel I K. The Kohonen network incorporating explicit statistics and itsapplication to the traveling salesman problem. Neural Networks, 1999, 12 (9): 1273-1284.

[16] ZHANG Wen-dong, BAI Yan-ping, HU Hong-ping. The incorporation of an efficient initialization method and parameter adaptation using self-organizing maps to solve the TSP. Applied Mathematics and Computation, 2006, 172 (1): 603-623.

[17] Latitude and longitude query of Chinese cities. [2013-01-11]. http://www.ximizi.com/jingweidu.php.

[18] Wang L. The neural network and combinatorial optimization. Doctor Thesis. Academy of Sciences, Beijing, 2000.

[19] WU Ling-yun. The application for Neural networks in combinatorial optimization and DNA sequencing. Doctor Thesis. Department of Mathematics, Academy of Sciences, Beijing, 2002: 46-50.

[20] Faigl J. On the performance of self-organizing maps for the non-Euclidean traveling salesman problem in the polygonal domain. Information Sciences, 2011, 181 (19): 4214-4229.

date： 2013-07-28

China Science Foundation (No.61275120)

SONG Jin-juan (123976518@qq.com)

1674-8042(2013)04-0353-08

10.3969/j.issn.1674-8042.2013.04.012