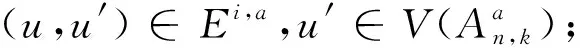排列图的若干k*-连通性
2013-12-18徐辉
徐 辉
(浙江师范大学 数理与信息工程学院,浙江 金华321004)
1 引言及预备知识
我们通常用一个连通的无向图G=(V;E)表示互联网络的拓扑结构,图G的顶点代表网络中的组件,图G的连线代表网络中组件之间的通信联系[1].星图是一个广泛研究的网络结构,而排列图是星图的一类分支,但它的阶却比星图更具有灵活性.排列图是点可迁图也是边可迁图,而且当n≥3,k=n-1时,它同构于星图;当n≥2,k=1时,它同构于完全图.
首先令n,k为两个整数,且1≤k
V={p=p1p2…pk|pi∈ 边集 E={(p,q)|∃唯一的i,使得pi≠qi,1 ≤i≤k}. An,k为k(n-k)-正则图.若p∈V,p=p1p2…pk,定义 EXT(p)= 称之为p的外元素,|EXT (p)|=n-k.[2] 若u,v是一个图G中的两个不同的点,且u,v存在图G中的k条内不交的路,则称这k条路为u,v间的k条容器,并记为k-(u,v)容器.若k-(u,v)容器的所有路中包含图G中所有的顶点,则称k-(u,v)容器为k*-(u,v)容器.∀u,v∈V(G),u与v间都存在k*-(u,v)容器,则称图G为k*-连通的.一个图G是k*-连通的,且1 ≤k≤κ(G),则称图G为超支撑连通图,其中κ(G)为图G的点连通度.根据上面定义,若一个图中的任何两点间都存在哈密顿路,则这个图为哈密顿连通图,即等同于1*-连通图;若一个图含有一个哈密顿圈,则这个图是哈密顿图,即2*-连通图. K Day和A Tripathi证明了当n≥2,n-k≥2时,排列图是哈密顿连通图[3],即排列图是1*-连通图.而且他们也证明了当n≥3,n-k≥1时,排列图是哈密顿图[4],即排列图是2*-连通图. 若(u,v),(u′,v′)是Ei,j中两条不同的边,{u,v}∩{u′,v′}=∅,则 性质2[5]k≥2,n-k≥2时,若u,v是An,k中的两个不同点,且d(u,v)=1,则|EXT (v)|=n-k-1,当k=1时,An,1≅Kn,Kn为完全图. 引理1[6]当n≥2时,An,1为超支撑连通图. 引理2[5]假定: (ⅰ)n≥4,n-k≥2,t是一个整数,且1 ≤t≤k; (ⅱ)I⊆ 定理1 当n≥5,n-k≥3时,An,k为3*-连通图. 证明当k≥2,n-k≥2时,An,k为哈密顿连通图,即∀u,v∈V(An,k),u,v间存在一条哈密顿路.同样,An,k也为一个哈密顿图,即图中存在一个哈密顿圈.证明An,k为3*-连通图,只要证明∀u,v∈V(An,k),An,k内存在3*-(u,v)容器.下面用分类讨论的方法来证明.主要分为两种情形:第一种情况是u,v属于同一个子图;第二种情况是u,v属于不同的子图. T1={u,P,v}, T2={u,Q,v}, T1,T2构成两条内不交的(u,v)-路. T3={u,u′,HP,v′,v}. 则T1,T2,T3构成u,v间的3*-(u,v)容器. u=u1u2…uk-1i, v=v1v2…vk-1j. 下面来构造u,v间的内不交的路. T1={u,P1,x,y,Q1,v}, T2={u,P2,x′,y′,Q2,v}. T3={u,u′,HP,v′,v}. 则T1,T2,T3构成u,v间的3*-(u,v)容器. 根据情形1和情形2就证明了定理1. 定理2 当n≥6,n-k≥3,An,k为4*-连通图. 证明类似于定理1的证明方法,An,k为4*-连通图,只要证明∀u,v∈V(An,k),An,k内存在4*-(u,v)容器.下面用分类讨论的方法来证明.主要分为两种情形:第一种情况是u,v属于同一个子图;第二种情况是u,v属于不同的子图. T1={u,P,v}, T2={u,Q,v}, T1,T2构成两条内不交的(u,v)-路. T3={u,w,HP1,z,v}. T3={u,w,HP1,z,v}. T4={u,u′,HP,v′,v}. 则T1,T2,T3,T4构成了4*-(u,v)容器. u=u1u2…uk-1i, v=v1v2…vk-1j. 下面来构造u,v间的内不交的路. T1={u,P1,x,y,Q1,v}, T2={u,P2,x′,y′,Q2,v}. T3={u,w,HP1,z,v}. T3={u,w,HP1,z,v}. T4={u,u′,HP,v′,v}. 则T1,T2,T3,T4构成了4*-(u,v)容器. 通过情形1和情形2就证明了排列图是4*-连通图. 参考文献: [1] 徐俊明.组合网络理论[M].北京:科学出版社,2007:100-102. [2]DayK,TripathiA.Arrangementgraphs:aclassofgeneralizedstargraphs[J].InformationProcessingLetters,1992,42(5):235-241. [3]DayK,TripathiA.CharacterizationofNodeDisjointPathsinArrangementGraphs[D].TechnicalReportTR91-43,ComputerScienceDepartment,UniversityofMinnesota,1991. [4]DayK,TripathiA.Embeddingofcyclesinarrangementgraphs[J].IEEETransactionsonComputers,1993,42(8):1002-1006. [5]DayK,TripathiA.Embeddingofcyclesinarrangementgraphs[J].IEEETransactionsonComputers,1993,42(8):1002-1006. [6]HsuH-Chun.TheSpanningConnectivityofthe(n,k)-StarGraphs[J].InternationalJournalofFoundationsofComputerScience2006,17(2):415-434.
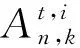

2 定理1的证明
2.1 情形1



2.2 情形2




3 定理2的证明
3.1 情形1
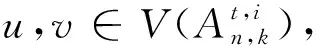



3.2 情形2