基于透射光谱确定硅碳氧薄膜的光学常数
2013-12-18王多书
张 平,李 晨,陈 焘,王多书
(1.台州学院 物理与电子工程学院,浙江 台州 318000;2.兰州空间技术物理研究所,甘肃 兰州 730000)
0 前 言
硅碳氧(SiCxO4-x)薄膜是一种含有Si、C和O三种元素的玻璃状化合物材料,同时拥有碳化硅薄膜及氧化硅薄膜多种优异的特性,如热稳定性好、能带宽、折射率大、硬度高和热导率高等.由于其优越的光学和力学性能,硅碳氧薄膜是一种更具潜在应用价值的新颖光学薄膜[1-2],可以用作硅基光电子器件、硅基太阳能电池的增透膜以及窗口层材料.作为功能型光学膜层,薄膜的光学常数(如折射率、 色散常数、厚度等)是其光学性能的直接体现,如何方便而准确地获得薄膜的光学常数对于其应用具有十分重要的意义.
测量薄膜光学常数的方法很多,通常分为非光学方法和光学方法两大类.非光学方法有着稳定性好、分辨率高和测量范围大等优点,但一般只用于测试薄膜的厚度,而且在测试过程中会对样品造成二次损害,限制了这类方法在光学薄膜测试中的应用[3].光学方法中应用最广泛的是光谱法和椭圆偏振法.椭圆偏振法在运用过程中需要的设备及计算模型都较为复杂,而且在测试薄膜厚度较小、折射率相近的样品时所得的结果偏差较大[3].1983年,Swanepoel[4]报道了一种基于透射光谱获得弱吸收薄膜光学常数的方法,该方法称为Swanepoel极值包络线法.由于透射光谱的测量精度比较高,因而该方法在确定弱吸收薄膜光学常数方面得到了广泛的应用[5-8].结果表明,该方法能够准确地得到薄膜的光学常数.
从透射光谱中可以看出,硅碳氧薄膜属于典型的弱吸收薄膜[2],适用于采用Swanepoel极值包络线法直接计算薄膜的光学常数,但未见相关报道.为此,本文试图根据硅碳氧薄膜的紫外、可见及红外透射光谱,采用Swanepoel极值包络线法结合WDD色散关系,建立一套精确、方便并适合于计算硅碳氧薄膜光学常数的方法.同时将薄膜厚度的计算值与实际结果进行比较,验证该方法的精确度.
1 试 验
本试验采用射频磁控溅射设备,以Ar作为工作气体、硅碳氧陶瓷靶作为溅射靶材,在K9玻璃上制备了硅碳氧薄膜,并经特殊处理在样品上做了一个台阶.在K9玻璃上沉积薄膜主要用于测试薄膜的透射光谱,所制作的台阶用于测试薄膜的厚度.试验前,使用超声波清洗机,把基片放在丙酮及无水酒精中各超声清洗15 min.所有试验本底压强均为3×10-3Pa,在打开挡板沉积薄膜前,利用等离子体轰击靶材10 min,便于清洗靶材表面及稳定等离子体.沉积薄膜时的工作压强为1 Pa,射频溅射功率为300 W,沉积时间为30 min.沉积时,基片温度保持在150±3 ℃.
最后,采用美国PerkinElmer公司生产的紫外/可见/近红外光度计(Lambda 900)获得了以K9玻璃为基片的样品在250~1 800 nm波长范围内的透射光谱,如图1所示.采用美国Veeco精密仪器有限公司Dektak 8探针式轮廓仪(台阶仪)测试了样品薄膜厚度,为619.2 nm.

图1 K9玻璃透射光谱(Ts)、硅碳氧薄膜透射光谱(T)及上包络线(TM)和下包络线(Tm)Fig.1 The transmission spectrum of SiCO thin film and substrate
2 结果与讨论
2.1 薄膜样品的透射光谱及光学常数计算方法
图1给出了K9玻璃及硅碳氧薄膜的透射光谱图.从图1中可以看出,K9玻璃在光谱测试范围内有较好的透射性能,并且透射率一致性也较好.硅碳氧薄膜的透射率随光波波长存在着振荡现象,这种变化源于光在两个界面即空气-薄膜及薄膜-基片界面的干涉现象[4].在吸收边附近,干涉带逐渐消失,且膜层的透射率由于本征吸收急剧下降.
对于沉积在具有一定厚度的透明基片上厚度均匀的薄膜,其示意图如图2所示(见下页).图中分别用ds和ns表示基片的厚度和折射率,用d和n表示薄膜的厚度和折射率,用α和κ表示薄膜的吸收系数和消光系数.根据Swanepoel[4]的观点,对于图2(见下页)所示的光学系统,应当满足d≪ds且κ2≪n2(弱吸收)的情况下,薄膜的透射率T可以用下式表示:
(1)
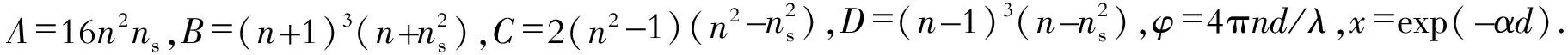

图2 沉积在具有一定厚度的透明基片上薄膜示意图Fig.2 The optical system of glass substrate with thin film
透射光谱干涉带的极值可分别表示为:
(2)
(3)
式(2)和式(3)中,透射光谱的上、下包络线TM及Tm可以看成是波长λ的连续函数,可以通过对样品透射光谱的极值进行拟合得到.在TM和Tm确定之后,联立上述方程,就可以很方便地获得薄膜的光学常数.采用包络线法计算光学常数时,要先将透射光谱按对不同谱段吸收的强弱分为弱吸收区、中等吸收区及强吸收区.在本研究中,我们划定波长λ≥800 nm为膜层的弱吸收区域,600 nm≤λ≤ 800 nm为中等吸收区域,λ≤600 nm为强吸收区域.
采用Swanepoel方法结合WDD色散模型确定薄膜光学常数的方法主要包括以下五步:(1)根据样品透射光谱,确定上、下包络线TM及Tm;(2)基于弱吸收和中等吸收区域的包络线计算该光谱区域内膜层折射率;(3)采用WDD色散模型对计算得到的折射率数据进行分析,获得色散常数;(4)将计算得到的折射率数据外推至强吸收区域,获得强吸收波段的折射率;(5)代入薄膜厚度计算公式获得薄膜厚度.
2.2 薄膜样品的折射率、 厚度和色散常数
对于弱吸收及中等吸收区(λ≥600 nm),折射率可以通过下式计算而得:
(4)

-C4+C5λ2/λ2-C6
(5)
式中,C1、C2、C3、C4、C5、C6分别是1.039 612 12、0.006 000 698 67、0.231 792 344、0.020 017 914 4、1.010 469 45、103.560 Y653.
由公式(5)计算得到硅碳氧薄膜样品的折射率数据如图3中实线所示.表1给出了薄膜透射光谱极大(小)值对应的波长、透射率及折射率.作为比较,在图3中还给出了由WDD色散关系推导获得的薄膜折射率数值,如图3中虚线所示.

图3 由包络线法及WDD色散关系获得的折射率随波长的关系Fig.3 The relationship,derived from Swanepoel’s theory and the WDD dispersion model,of wavelength and refractive index
由于式(1)是在κ2≪n2(弱吸收)的条件下得到的,对于强吸收区,该公式将不再适用,该区域的折射率数值可由WDD单振子色散模型得到.WDD单振子色散模型是Wemple[9]等在1971年提出,认为折射率与单振子能量E0及散射能量Ed存在如下关系:
(6)
根据式(6)及已获得的折射率数据,作(n2-1)-1随E2的变化曲线,并进行线性拟合.然后根据该直线的斜率与y轴的交点可以获得E0与Ed.并且根据拟合的直线向强吸收区域外推,便可得到该区域薄膜的折射率.
图3内的插图为WDD色散关系图.插图内的实线为拟合的直线.可以看出,所获得的结果和直线拟合得较好,表明采用WDD色散模型研究所讨论的薄膜体系是合理的.根据线性拟合结果,得到薄膜的E0和Ed值分别是5.2 eV和13.9 eV.
将式(6)外推至短波区域,即可估算出强吸收区域薄膜的折射率,如图3中虚线所示.在光谱的强吸收区域,两种方法获得的折射率差异较大,是由于包络线法不再适用造成的.
采用上述计算得到的折射率数据,可以根据式(7)得到一系列薄膜厚度:
(7)
式中,n1、n2为透射光谱中两个相邻的极大值(极小值)λ1、λ2处对应折射率,且有λ1>λ2.计算结果如表1所示,对薄膜厚度计算的平均值为606.8 nm,相对标准方差为2.41%.测试的薄膜厚度值为619.2 nm.结果表明,根据本方法计算获得的薄膜厚度与测量值比较接近,两值相对误差仅为2.0%.从而间接验证了该方法可以较为准确地获得薄膜的折射率、厚度等光学常数.

表 1 薄膜折射率及厚度计算结果Tab.1 The calculated values of refractive index and thickness
3 结 论
基于硅碳氧薄膜的透射光谱,根据Swanepoel极值包络线法以及WDD色散模型,建立一套精确、方便并适合于计算硅碳氧薄膜光学常数的方法.结果显示,在透射光谱的弱吸收区,两种方法给出的结果有极好的吻合性,表明采用Swanepoel极值包络线法以及WDD色散模型来研究硅碳氧薄膜光学常数的计算是合理的.薄膜厚度的计算值与实际测量值相对误差仅为2.0%,更进一步验证了该方法的准确度及可靠性.该工作有益于指导硅碳氧薄膜的制备及应用研究.
参考文献:
[1] 张平,罗崇泰,陈焘,等.碳化硅薄膜制备方法及光学性能的研究进展[J].真空与低温,2009,15(4):193-198.
[2] 李晨,陈焘,王多书,等.硅碳氧薄膜光学性能研究[J].真空科学与技术,2012,32(8):732-735.
[3] 陈燕平,余飞鸿.薄膜厚度和光学常数的主要测试方法[J].光学仪器,2006,28(6):84-88.
[4] Swanepoel R.Determination of the thickness and optical constants of amorphous silicon[J].JPhys,1983,16:1214-1222.
[5] 梁丽萍,郝建英,秦梅,等.基于透射光谱确定溶胶凝胶ZrO2薄膜的光学常数[J].物理学报,2008,57(12):7906-7911.
[6] Ilican S,Caglar M,Caglar Y.Determination of the thickness and optical constants of transparent indium-doped ZnO thin films by the envelope method[J].MaterialsScience-Poland,2007,25(3):709-718.
[7] Shaaban E R.Optical characterization of arsenic sulfide semiconducting glass films using the transmittance measurements[J].MaterialsChemistryandPhysics,2006,100:411-417.
[8] Xu Yu,Shen Mingrong.Structure and optical properties of nanocrystalline BiFeO3films prepared by chemical solution deposition[J].MaterialsLetters,2008,62:3600-3602.
[9] Wemple S H,DiDomenico M.Behavior of the electronic dielectric constant in covalent and ionic materials[J].PhysicalReviewB,1971,3(4):1338-1351.
