巷道变形及衬砌受力的影响因素敏感性分析

冯 伟，韩立军，张帆舸，任光住

(1.中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116；2.中国矿业大学力学与建筑工程学院,江苏 徐州 221116)

随着我国煤矿资源开采规模和深度的不断加大，巷道所赋存的地质力学环境越来越复杂，对于维持巷道围岩稳定性提出了新的挑战。巷道变形及支护构件受力主要受3方面因素的影响：巷道围岩地质条件；巷道工程赋存环境；巷道施工因素[1]。而这些因素对巷道变形及支护受力产生的影响都是通过改变巷道围岩状态(弹性、塑性及破裂状态)来实现的[2]。影响巷道变形及支护受力的参数往往具有随机性、不确定性的特点，且各参数的变化对其影响程度以及变形及支护受力对何种因素的影响最为敏感往往是工程关心的重要问题，因而有必要通过一定研究来获得巷道变形及支护受力对各个因素的敏感程度，为评价巷道稳定性及确定定量化工程支护措施提供依据[3-4]。

目前针对多因素实验分析多采用正交实验的方法，有关巷道围岩稳定性的多因素试验研究，有人已经做了许多有价值的工作[2-9]，主要集中于岩体的强度参数及变形参数对巷道围岩塑性区、变形量、岩层控制的影响。有研究表明，弹性模量及泊松比对巷道变形产生显著影响，而强度参数黏聚力及内摩擦角是影响围岩塑性区及变形量的主要因素[10]。研究方法多是采用正交试验与数值模拟相结合，但研究内容多侧重于未支护巷道，且较少考虑初始应力场的影响，与巷道实际的受力条件不同。本文采用正交数值模拟试验，统筹考虑巷道应力场、岩性参数及支护作用等因素，根据级差分析了不同因素对巷道变形及支护衬砌受力的影响显著程度。

1 正交数值模拟试验

1.1 数值模型

本文采用ABAQUS 数值计算软件作为分析工具。研究直墙半圆拱形巷道在不同试验条件下巷道变形及衬砌受力规律。试样模型尺寸50m×50m，半圆拱形巷道宽4m，高3.6m。模型左右两侧1方向的位移U1=0，底面上3方向的位移U3=0，顶面为应力边界，在上边界施加垂直应力来模拟上覆岩层。采用平面应变模型，模拟巷道开挖前，先采用ABAQUS中geostatic分析步进行初始地应力的平衡。巷道支护方案：Φ20mm螺纹钢间距0.8m，长度L=2.4m，全长锚固，预应力30kN；考虑巷道开挖后应力释放：采用刚度折减法，先释放70％的围岩压力，再施作衬砌和预应力锚杆。支护构件力学参数见表1。

图1 数值计算模型

表1 支护构件力学参数

模型为单一均质材料,其物理力学性质见正交试验安排。选用理想弹塑性模型,采用Mohr-Coulomb屈服准则。

由Mohr-Coulomb屈服函数可以得到剪切破坏准则

式中：σ1，σ3分别是最大和最小主应力；c,φ分别岩体黏聚力和内摩擦角，当fs<0时，岩体将发生剪切破坏。

1.2 正交试验设计

多因素作用分析时，采用正交实验方法，可以用尽量少的实验得到最优的实验结果，且正交实验不同因素不同水平在实验中出现次数相同，任何因素不同水平搭配在实验中都将出现，因此，可以正确全面反映各因素各水平对目标的影响程度[11]。

根据影响巷道变形及衬砌受力的影响因素，以及所采用的Mohr-Coulomb屈服准则，选取埋深、侧压力系数、弹性模量、泊松比、黏聚力、内摩擦角6因素作为正交试验的因素。选用6因素5水平正交实验表，各因素取值如表2。根据正交实验设计原理和方法，共进行25次数值模拟实验，具体实验安排见表3。

表2 正交数值模拟实验因素方案

根据表2建立相应的数值计算模型,每个模型试验条件按照对应的试验号确定，其余模型条件不变。因为本次试验主要是研究巷道所处应力场及力学参数对巷道变形及支护构件受力的影响,衬砌受力采用地层-结构法计算，能够较为准确的反映围岩压力变化及支护构件受力情况，故取出每个模型的巷道变形量和衬砌受力作为试验结果。巷道变形量取巷道顶、底板移近量及两帮移近量之和,衬砌受力采用衬砌最上端单元的轴力来表示,试验结果如表3所示。

2 正交数值模拟试验结果分析

直观分析法是通过对每一因素的平均极差来分析问题,极差大小反映了该因素选取不同的水平变动对指标的影响大小。[12-13]有一正交表Lp(nm),其中n为各因素的水平数，p为试验总数， 试验的p个结果为服从正态分布的随机变量，分别为y1，y2,…yp。一般地，定义Kij为因素j的第i个水平的数值之和(i=1，2…n，j=A，B…) ，它是因素j在i水平下的统计参数。

极差是指一组数据中的最大数据与最小数据的差，它反映了一组数据的离散程度，表达式见式(2)。

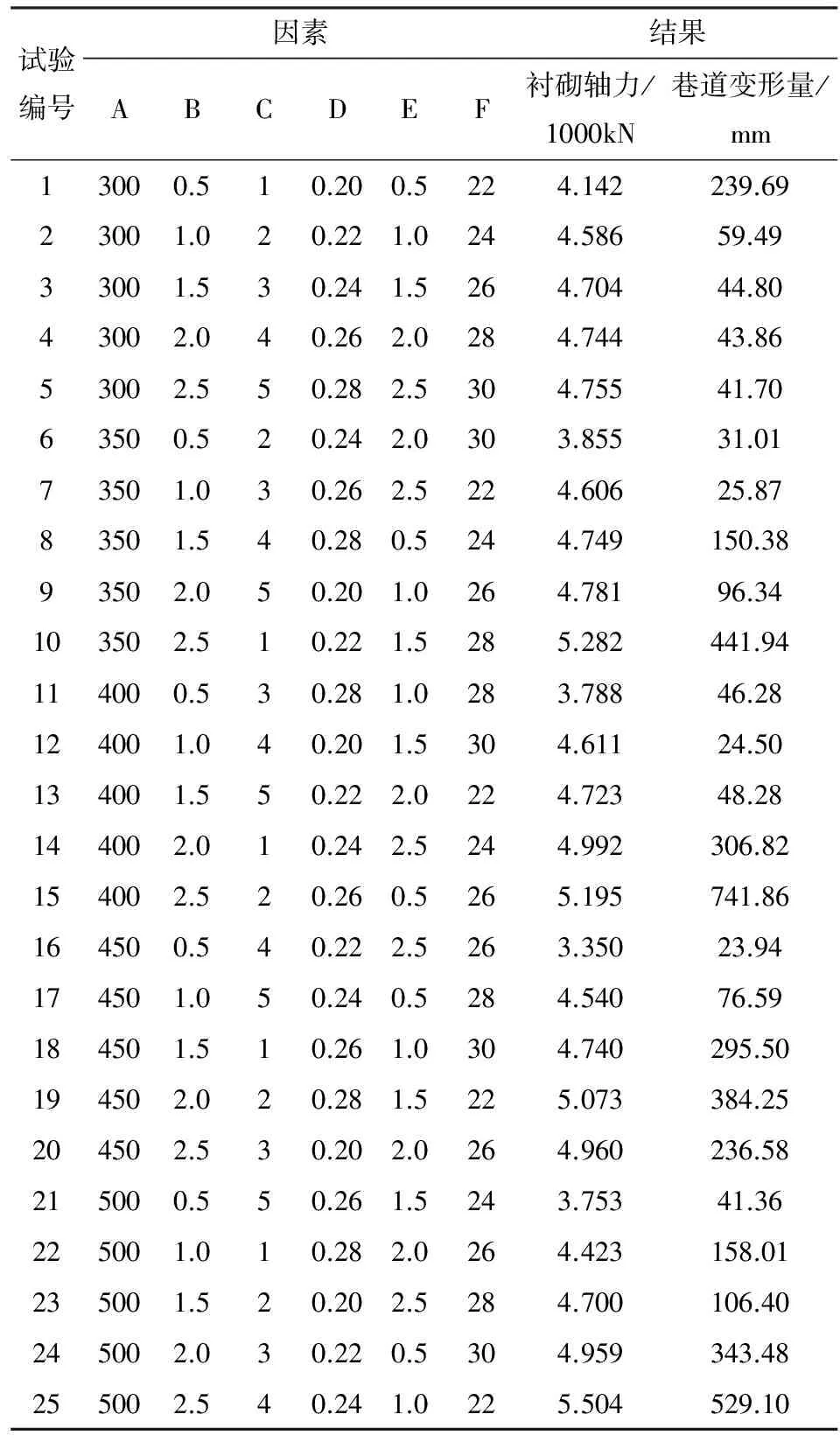
表3 正交数值模拟试验方案

根据表4不同因素极差，侧压力系数对衬砌轴力影响最大，内摩擦角、黏聚力、弹性模量对衬砌受力产生一定影响，泊松比影响较小，考虑到本文埋深较小，在埋深小于500m时，埋深对衬砌受力影响很小。根据表5不同因素极差，侧压力系数对巷道变形影响最大，黏聚力、弹模对巷道变形产生一定影响，内摩擦角、泊松比影响较小，在埋深小于500m时，埋深对巷道变形影响较小。

为进一步“量化”分析不同因素对衬砌轴力及巷道变形的影响，根据表4、表5得出了不同因素衬砌轴力及巷道变形均值随各水平变化见图2 、图3。

由表4、表5和图2、图3可得出如下结论。

1) 相比于围岩的力学参数侧压力系数是影响巷道衬砌受力和变形最显著性因素，随侧压力系数的增大，巷道衬砌轴力和变形都迅速增大。侧压力系数由1增加到1.5，衬砌受力由4553kN 增至4723kN,巷道变形由69mm增至129mm,不同侧压力系数将对巷道围岩的应力分布产生显著影响，从而对巷道变形破坏特征产生重大影响，因此布置巷道时，要首先考虑最大水平应力的方向及与竖向应力的比值，合理的确定巷道的层位与走向，其次再考虑巷道岩性的不同。

2) 巷道埋深在小于500m时,巷道深度的增加对于衬砌受力影响很小，但对巷道变形有一定的影响，由此可知在一定深度内围岩压力受埋深影响较小。随着埋深增加，巷道围压增大，使岩体强度适量提高，围岩承载性能提高，因而作用于衬砌上的力变化不大。

3) 弹性模量的增加使围岩抵抗变形的能力增加，有利于减小巷道变形量。其对巷道变形的影响程度要大于对衬砌轴力的影响程度。泊松比对衬砌受力及巷道变形量影响都较小。

4) 黏聚力和内摩擦角是岩体重要的力学参数，随着黏聚力和内摩擦角增大，岩体强度提高，衬砌轴力和巷道变形都不断减小。但内摩擦角对衬砌轴力的影响程度较大，而黏聚力对巷道变形影响较大。且内摩擦角存在临界值，当内摩擦角小于24°时，对巷道衬砌轴力和变形影响较大。

表4 衬砌轴力直观分析

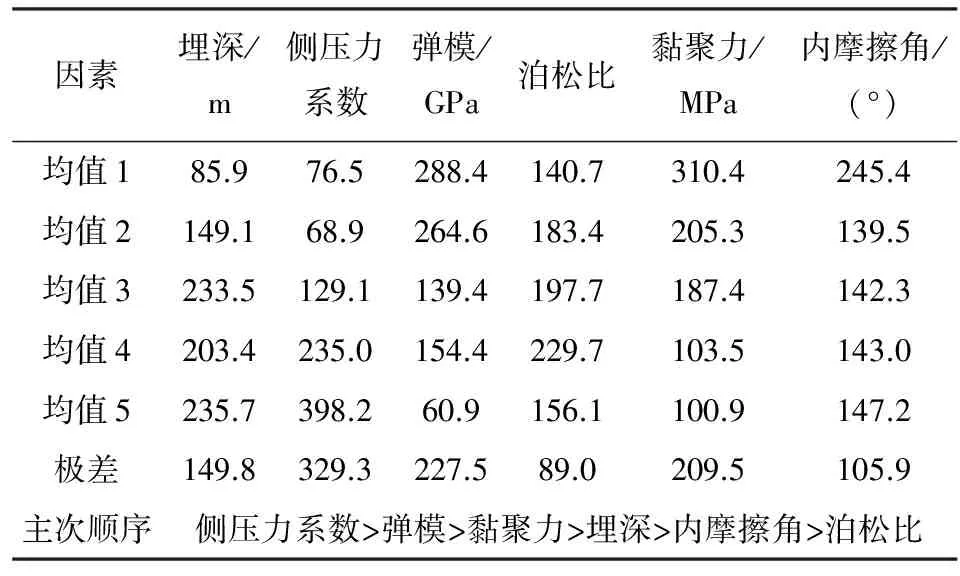
表5 巷道变形量直观分析

图2 各因素对衬砌轴力的影响

图3 各因素对巷道变形的影响

3 结论

采用正交数值模拟的方法对影响巷道衬砌受力和巷道变形的因素进行了多因素敏感性分析，得出了各影响因素的主次关系。 侧压力系数相对于岩性条件是影响巷道变形和衬砌受力更为显著性的因素，布置巷道时应根据实测地应力大小和方向，合理选择巷道的层位和走向。衬砌受力和巷道变形量对于各参数在一定范围内的摆幅表现出相同的变化趋势，但各参数对于衬砌受力和巷道变形量的敏感程度不同，在确定巷道定量的支护设计方案以及做反分析研究时，要统筹考虑各种因素的影响并应有所侧重。

[1]康红普.煤巷锚杆支护成套技术研究与实践[J].岩石力学与工程学报,2005,24(21):3959-3964.

[2]靖洪文，李元海，许国安.深埋巷道围岩稳定性分析与控制技术研究[J].岩土力学,2005,26(6):877-880,888.

[3]聂卫平，徐卫亚，周先齐.基于三维弹塑性有限元的硐室稳定性参数敏感性灰关联分析[J].岩石力学与工程学,2009,28(Z2):3885-3893.

[4]尤冰，李广杰.基于正交试验的巷道位移影响度研究[J].地下空间与工程学报,2011,7(Z2):1630-1633,1659.

[5]付建军,刘泉声,刘宾.基于数理统计的巷道塑性区边界分析[J].采矿与安全工程学报,2009,26(1):70-73.

[6]高富强,王兴库.岩体力学参数敏感性正交数值模拟试验[J].采矿与安全工程学报,2008,25(1):95-98.

[7]高富强,李志刚.影响巷道变形与破坏节理力学参数的正交数值模拟试验研究[J].山东科技大学学报：自然科学版,2008,27(1):5-10.

[8]于全发,贺俊征,王在泉，等.多元线性回归在矿体开采中的应用 [J].西安科技大学学报,2007,27(4):555-558.

[9]孙晓光,周华强,何荣军.基于蚁群算法和神经网络的位移反分析[J].西安科技大学学报,2007,27(4):569-572.

[10]黄书岭，冯夏庭，张传庆.岩体力学参数的敏感性综合评价分析方法研究[J].岩石力学与工程学报,2008,27(Z1):2624-2630.

[11]王永秀，毛德兵，齐庆新．数值模拟中煤岩层物理力学参数确定的研究[J]，煤炭学报，2003，28(6)：593-597.

[12]崔广心．相似理论与模型试验[M]．北京:中国矿业大学出版社，1989．

[13]《正交试验法》编写组.正交试验法[M].北京:国防工业出版社,1976.