保偏光纤中在不同频率区域拉曼效应和参量放大增益谱*

2013-12-12柴宏宇贾维国韩凤门克内木乐杨军张俊萍

物理学报 2013年4期

柴宏宇贾维国韩凤门克内木乐杨军张俊萍

(内蒙古大学物理科学与技术学院,呼和浩特 010021)

(2012年7月7日收到;2012年9月22日收到修改稿)

1 引言

保偏光纤是一种对线偏振光具有较强的偏振保持能力的光纤,而高双折射光纤是一种重要的保偏光纤,具有良好的偏振保持能力,并且与单模光纤有很好的相容性,在光子器件的偏振保持、光纤陀螺仪偏振保持、光纤环等领域具有广泛应用前景[1−3],在光纤激光器、光纤传感器、光波分复用器件以及相关光通信领域也有着十分广泛的应用[4,5].激光脉冲在双折射光纤中传输时,当脉冲达到一定强度,不但会产生参量放大(OPA)和拉曼散射效应(RSE),而且还会在光纤中产生热效应;强双折射光纤中,在拉曼散射和参量放大同时存在的情况下,斯托克斯波和反斯托克斯波的相关性质是由受激拉曼散射和参量放大共同决定.因此,研究参量放大和拉曼散射共同作用时增益系数随相关参量的变化,对于光纤开关和频率转换具有现实意义[6−8].热效应会使光纤中的温度产生变化,从而对波长产生影响,温度高波长就会变长.由于高双折射光纤的各向异性,导致在两偏振方向升温不同,从而使两偏振方向上的中心波长产生偏差,所以即使输入两个频率相同的抽运波,在传输过程中两偏振方向上也可能出现频率差,因而导致两双折射轴的波长不同,会影响相关保偏光纤器件的性能.例如,用保偏光纤绕制的光纤陀螺作为一种光纤传感器具有性能稳定、精度较高的特性,但随着光波在光纤中的传输,由于在两偏振方向上增益的不同,导致变化不一致,这些干扰在光纤长度上积分的效果会对光纤环产生相位调制,从而产生非互易性相移成为影响光纤陀螺漂移的主要因素之一[9].在保偏光纤偏振器中,利用保偏光纤的两个偏振模的特性,使得在光纤中传输的一偏振模在光波导处于截止状态,另一偏振模处于传输状态,从而使光纤达到起偏作用.若考虑上述因素,在传输过程中使工作波长发生漂移,首先影响偏振器的正常工作,其次由于传播常数差的变化会造成模的耦合,使保偏光纤两个正交的偏振态之间产生交叉偏振,从而产生损耗[10].

基于高双折射光纤中OPA和RSE,相关作者研究了输入抽运波偏振方向同双折射轴成45°时拉曼效应和参量放大共同作用所导致的增益及相关特性[11,12].本文利用拉曼效应和参量放大共同作用下在双折射光纤中所遵循的耦合模方程[11,12],并引入平行拉曼增益的洛伦兹模型,讨论了当入射两个波长不同的光脉冲,偏振方向互相正交且平行于光纤双折射轴时,在拉曼效应和参量放大共同作用下正常色散区和反常色散区所产生的增益特性.

2 理论分析

考虑拉曼效应,当入射两个波长不同偏振方向互相正交且平行于光纤双折射轴的光脉冲时,两束不同频率的光脉冲在光纤中传输时所满足的相干耦合薛定谔方程为[11,12]

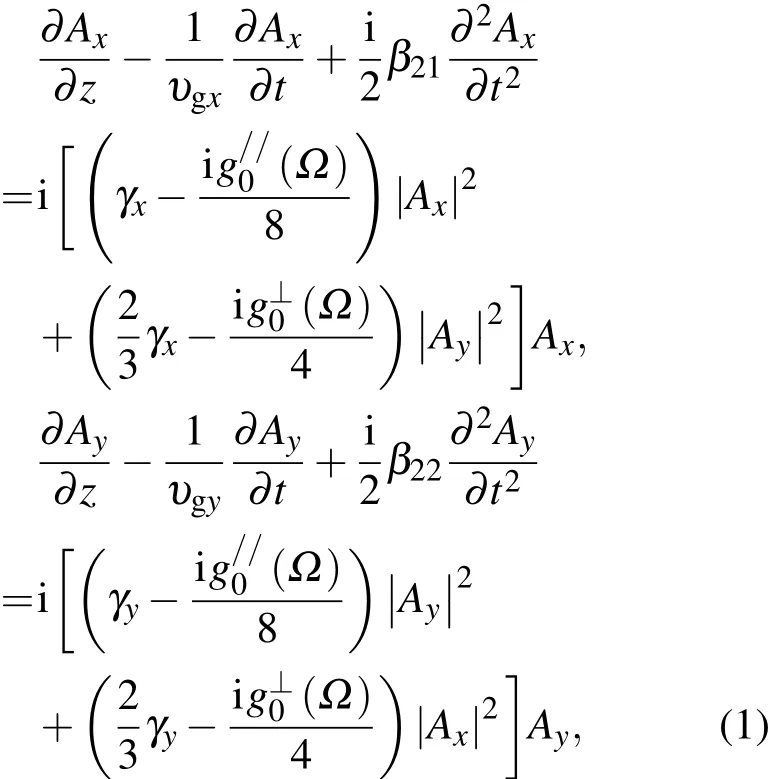
其中Ω表示抽运波和斯托克斯波或反斯托克斯波的频率差,对于斯托克斯波Ω=(ω0−ωs)＞0,而反斯托克斯波Ω=(ω0−ωa)＜0.在平行和垂直于抽运波偏振方向的x,y方向均产生拉曼增益,定义平行于抽运波偏振方向拉曼增益为平行拉曼增益g(Ω)=16iπωpχ(Ω)/c2kpAp的虚部,垂直于抽运波偏振方向拉曼增益为垂直拉曼增益gΩ)=16iπωχ/c2k p A p 的虚部,χ为平行于x轴的抽运波分量在x轴方向上的拉曼极化率,χ可看作是y方向的抽运波分量在x轴方向产生的拉曼极化率,且非线性极化率有如下关系:χ=χ;垂直拉曼增益取常数 g(Ω)≈ 0.1 m/W,平行拉曼增益系数g(Ω)采用洛伦兹模型:

其中系数 fR=3.125 THz,ωγ=8.2 THz.并定义非线性系数Ax为沿x方向上输入的抽运波的振幅,Ay为沿y方向上输入的抽运波的振幅,υg为群速度,为二阶色散系数,z为传输距离.由于输入的为两束不同波长的光波,所以,γx̸=γy,β21 ̸=β22.

为得到混合模抽运的稳态解,引入微扰u,v;u为x方向上的微扰,包含有两个成分:斯托克斯成分us,反斯托克斯成分ua;同理,y方向的微扰亦包含vs,va.引入微扰后的方程组(1)的稳态解为

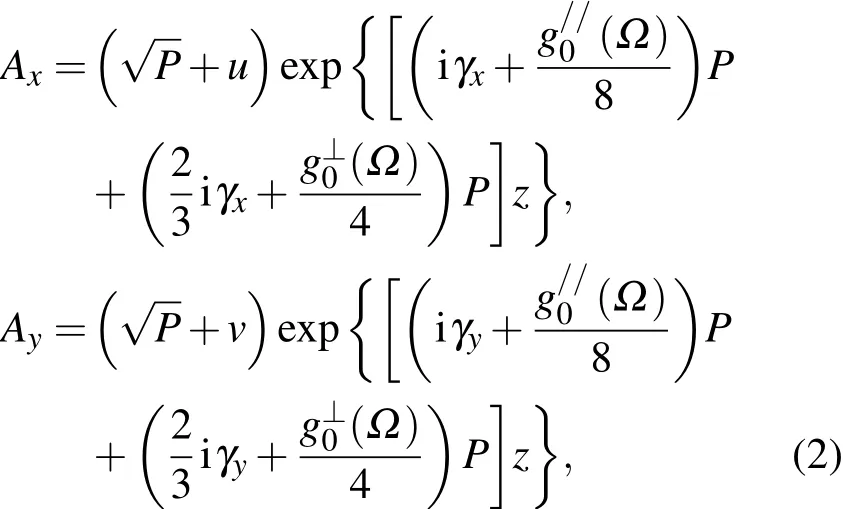
P为输入功率,设两束光的输入功率相同.将方程(2)带入方程(1)线性化,并采用群速度坐标系,得到关于微扰u,v的方程:

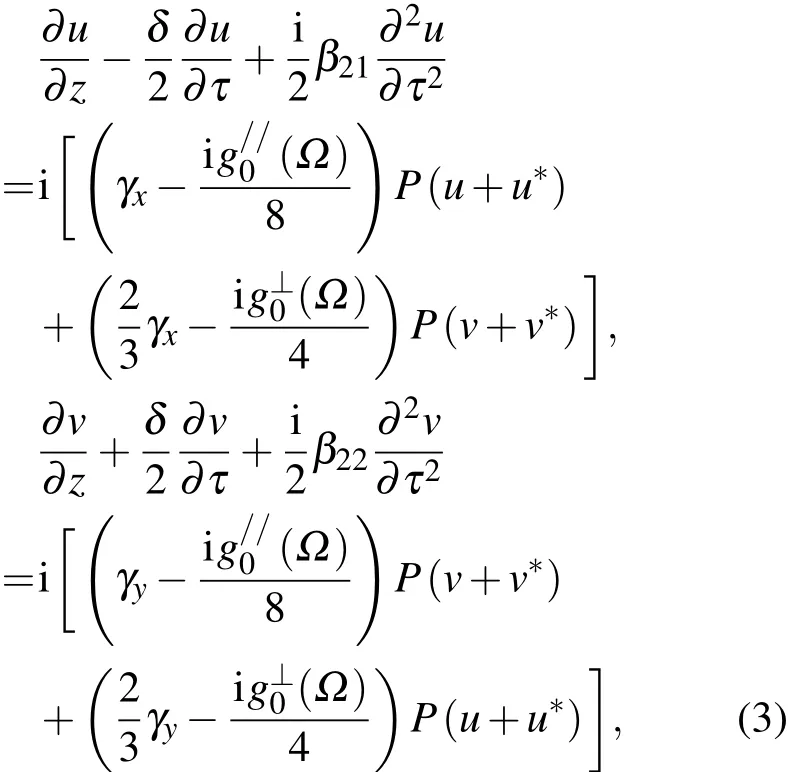
求解方程(3)时将微扰调制写成特解形式

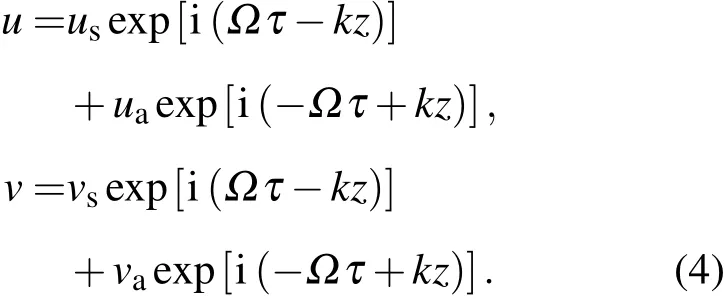
将特解(4)式带入方程(3)中,可化为下面的矩阵方程组形式:

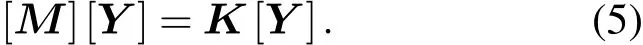
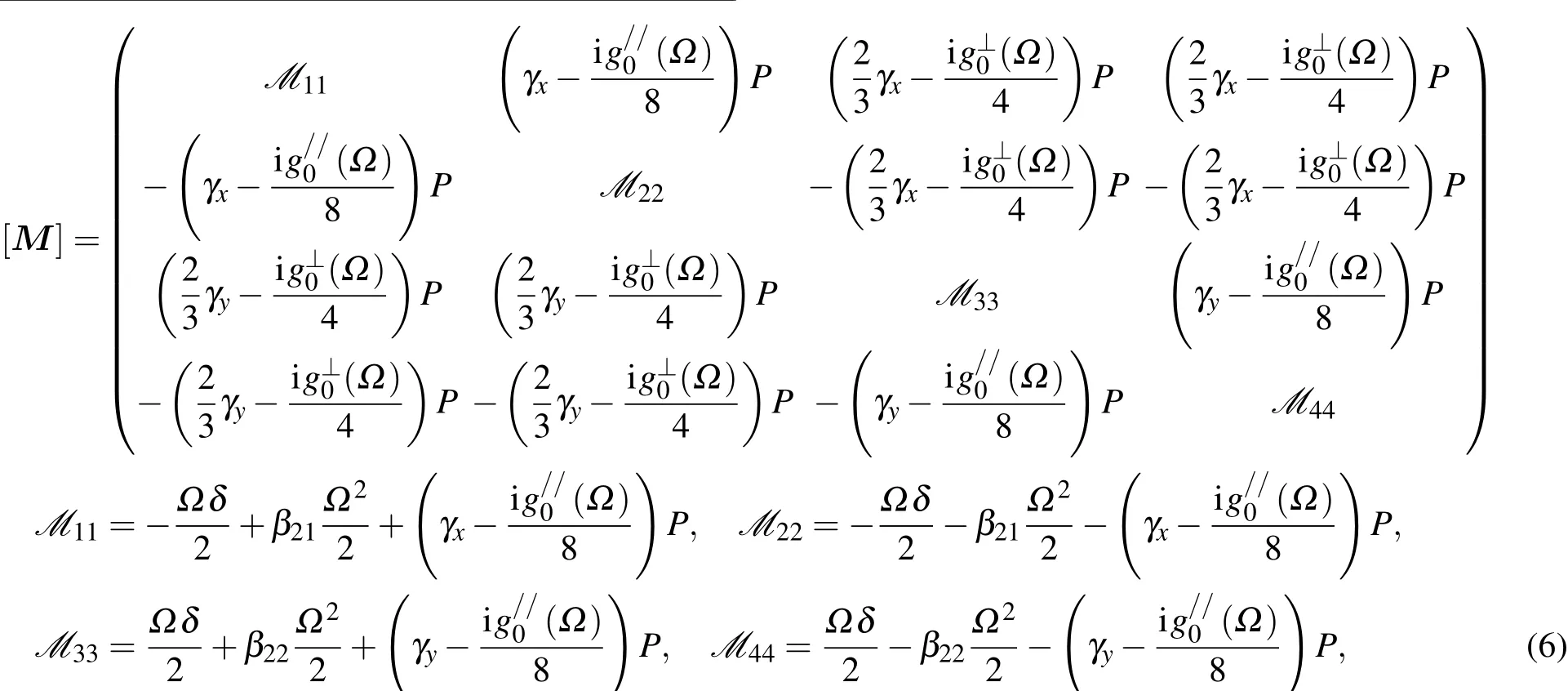
矩阵方程组(5)有解的条件为序数行列式等于0,得下面方程:

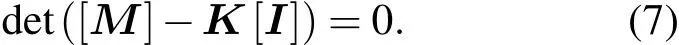
因此将一阶色散系数 β21=|β21|sgn(β21),β22=|β22|sgn(β22),非线性系数 γx,γy代入方程 (7),当沿着快轴和慢轴的光脉冲波长差小于10nm时,可以忽略方程中的K的一次项[13],转换为K2的一元二次方程,从而可以解得:

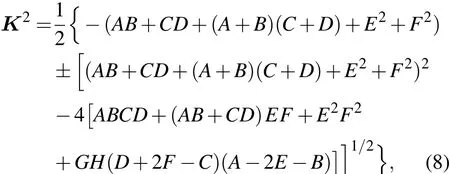
式中:

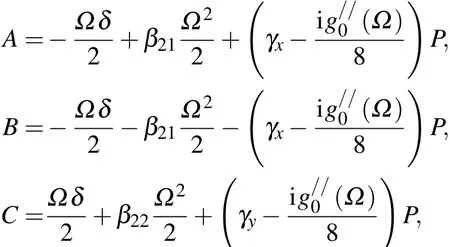
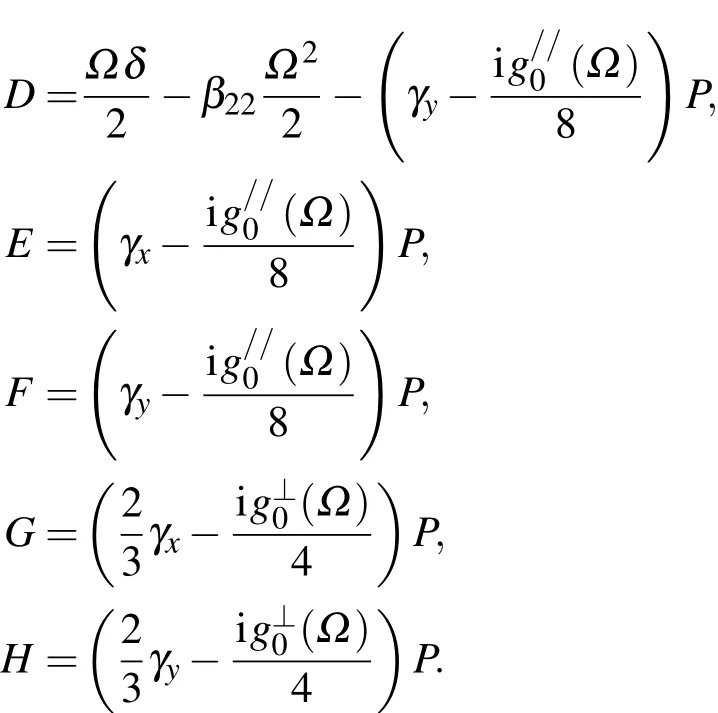
经带入化简可得:AB+CD+(A+B)(C+D)+E2+F2＜0,所以只有满足 ABCD+(AB+CD)EF+E2F2+GH(D+2F−C)(A−2E−B)＜0时,K 有复数解时,能产生增益,定义增益为

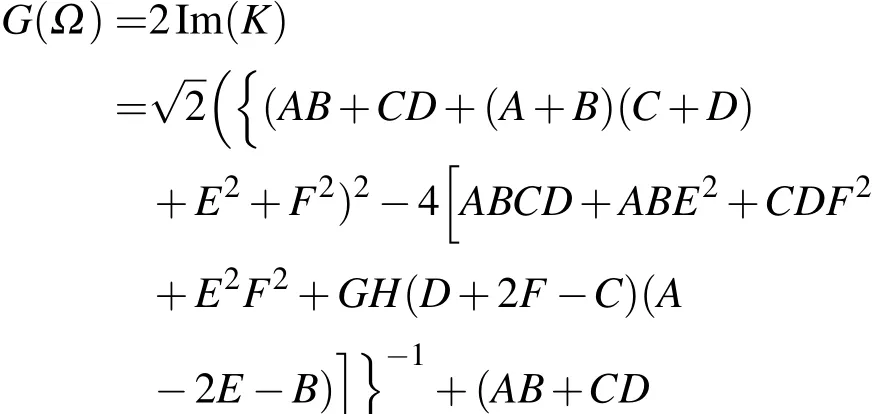
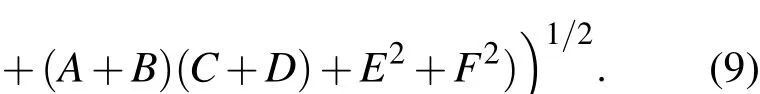
当输入两束不同频率激光脉冲时,用选取非线性系数 γx=25 W−1·km−1,γy=26 W−1·km−1,二阶色散系数β21=65 ps2/km,由于两偏振方向上的传输波长相差很小,群速度色散随波长减小而线性增加,所以β22与β21的差别不太大,与波长差有关,当波长差为2 nm时取β22=66 ps2/km.输入两束相同频率的激光脉冲时选取非线性系数γ=25.8 W−1·km−1,二阶色散系数β2=65 ps2.

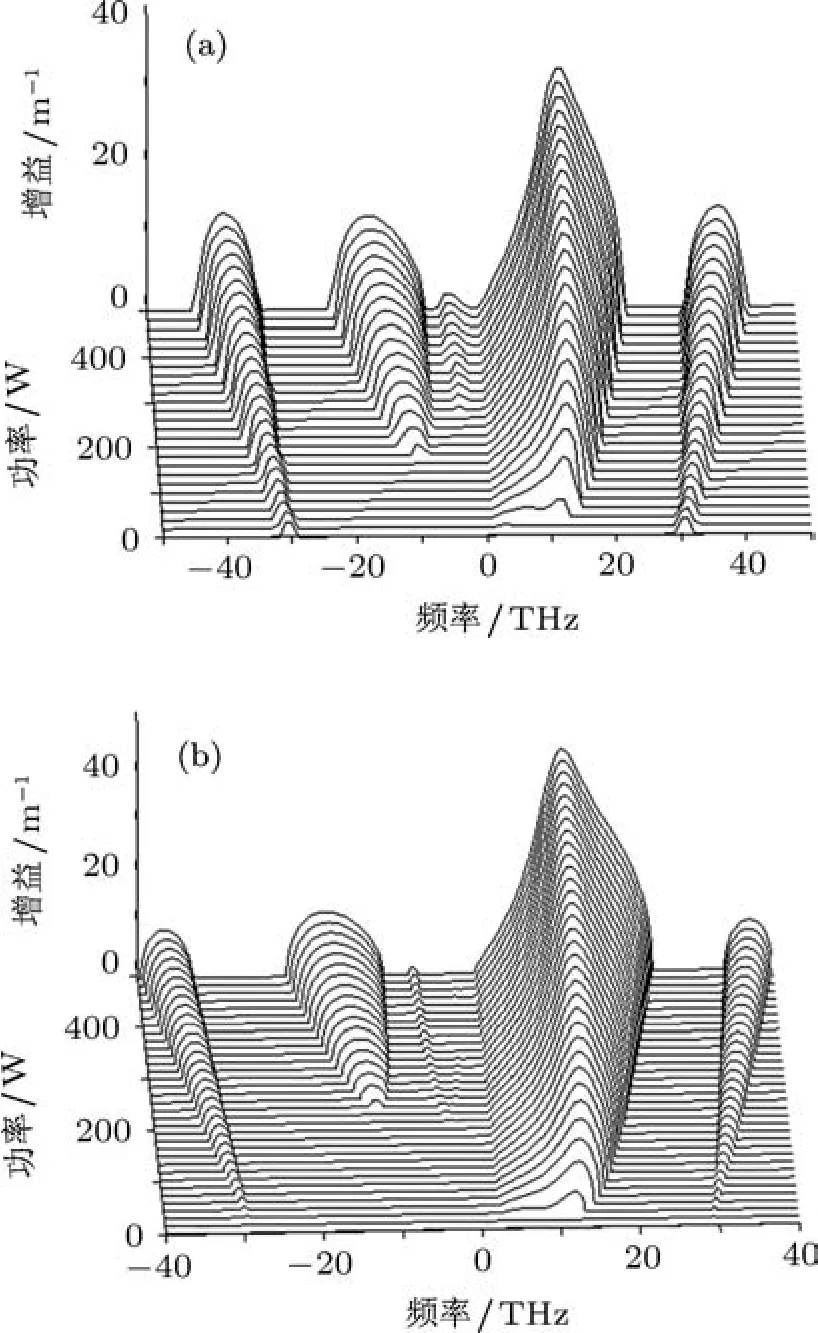
图1 同为正常色散区考虑拉曼效应时,输入两束不同和相同频率激光脉冲时,增益随频率和功率的变化关系 (a)不同频率;(b)相同频率

2.1 两者同为正常色散区

当两色散系数同为正常色散区时β21,β22同为正数,群速度失配为δ=1.9 ps/m时,输入相同频率激光脉冲和输入不同频率激光脉冲的增益随功率的变化关系如图1所示.可以看出沿互相正交且平行的光纤双折射轴,不论输入的两激光脉冲频率是否相同,在考虑拉曼效应的条件下增益在反斯托克斯(频率差小于零)部分和斯托克斯部分(频率差大于零)变化是不对称的.不同频率(图1(a))和相同频率(图1(b))的整体变化趋势相同,在斯托克斯部分同为双峰结构,反斯托克斯部分为多峰结构.在靠近中心频率的两侧,两图都呈现出斯托克斯部分的增益强于反斯托克斯部分,并且不同频率的斯托克斯波主峰弱于相同频率斯托克斯波主峰.在远离中心频率的外侧,差别比较明显,输入不同频率激光脉冲所产生的增益略强于输入相同频率激光脉冲时产生的增益.在输入不同频率激光脉冲,功率较小时,在外侧存在两个对称的增益峰,而输入频率相同时,当功率达到一定值时才出现增益.

群速度失配为δ=1.9 ps/m,输入功率恒定为P=250 W时可得到增益随波长差的变化关系图2.

从图2可以看出,随着波长差的增加,增益谱的宽度和强度都略有增强,但整体的形状没有什么变化.

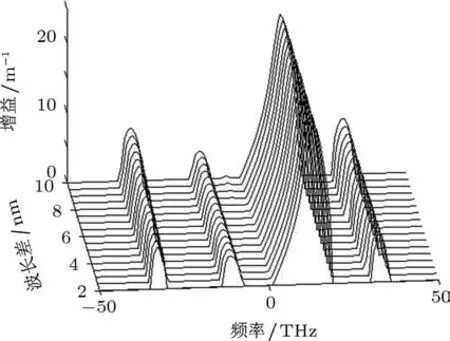
图2 在正常色散区,输入功率和群速度失配恒定时,增益随波长差的变化关系

两偏振方向的输入功率恒定为P=250 W时,可以得出增益随群速度失配的变化关系为图3所示.

从图3中可以看出,输入相同频率的激光脉冲和输入不同频率的激光脉冲产生的增益图整体形势基本相同,区别在于不同频率的增益峰的强度和宽度稍大于相同频率的情况.对于输入不同频率激光脉冲(图3(a)),在群速度失配较小时,中心频率两侧的两个增益峰强度和宽度基本不随群速度失配变化,随着群速度失配的增加,这两个增益峰开始变化分离为两部分;在靠近中心频率的斯托克斯部分出现一个强度较强、宽度较宽,随着群速度失陪的增加,分裂为两部分的增益峰,开始时有一段强度明显的下降,随后保持相对稳定.另一个增益峰强度较弱、宽度较窄,且强度和宽度最初缓慢下降,随后强度稳定不变,方向随群速度失配增大远离中心频率.在反斯托克斯部分,随群速度失配的增大,分离出三个不同的增益峰,向中心频率方向偏移的增益峰较相同频率情况较弱,并且很快消失;远离中心频率的增益峰其强度和宽度较相同频率时的情况较大,相对稳定,在三者中强度最强;中间的增益峰其强度和宽度大于相同频率是对应的增益峰,呈缓慢增加趋势;对于向远离中心频率方向偏移的两个增益峰的频率属于太赫兹脉冲,利用其远离中心频率分离的特性,可以提取太赫兹脉冲.

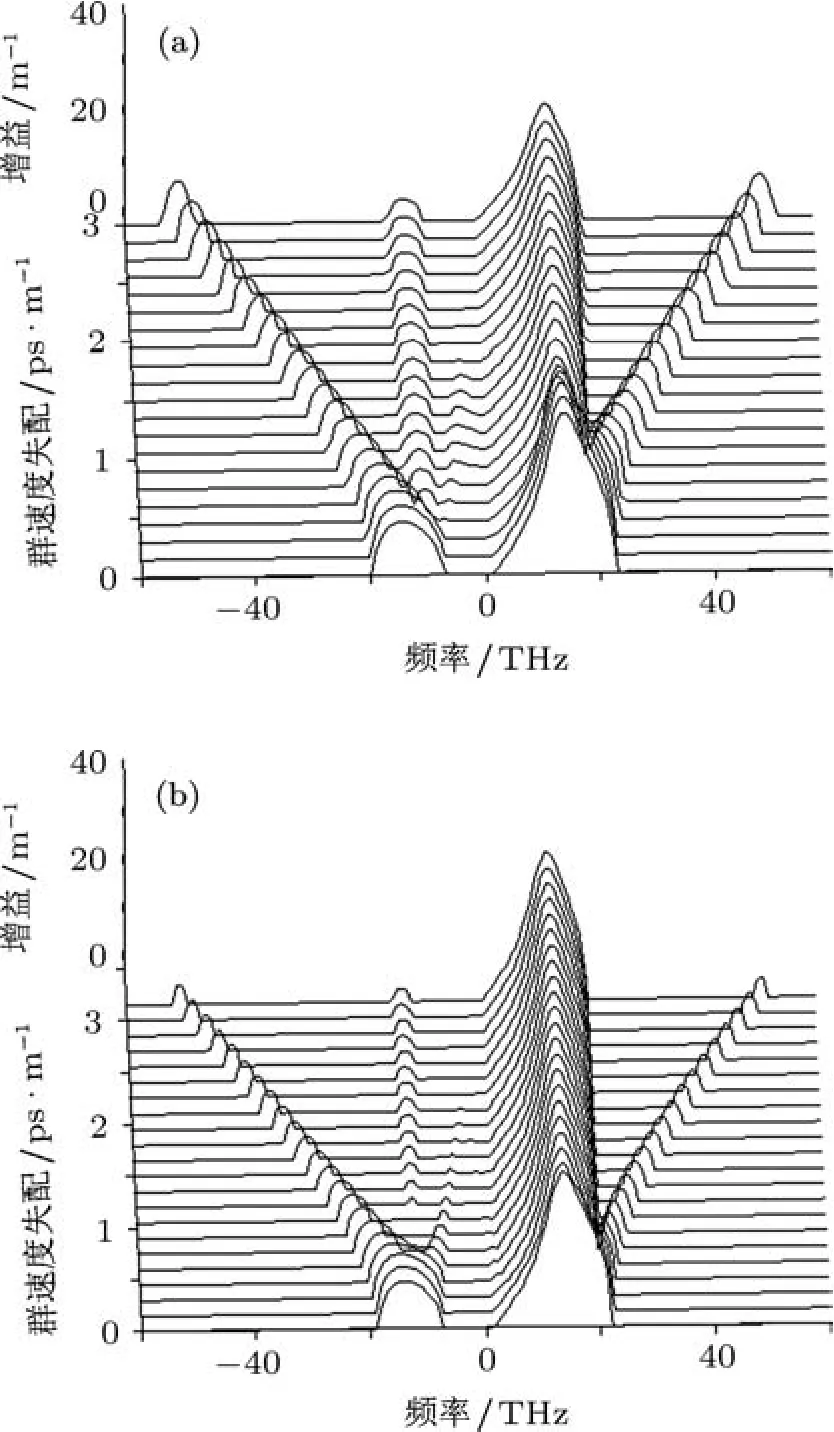
图3 同为正常色散区考虑拉曼效应时,输入两束不同和相同频率激光脉冲时,增益随频率和群速度失配常数的变化关系(a)不同频率;(b)相同频率

2.2 两者同为反常色散区

当两色散系数同在反常色散区时色散系数为负数,参数绝对值同在正常色散区时相同.图4为在拉曼效应和参量放大共同作用下,不同频率和相同频率时,增益随频率和功率的变化.两图在斯托克斯部分同为复杂的多峰结构,最内侧紧贴中心频率处都存在一个小的增益峰,宽度和强度随功率的增加变化不大,外侧的差别较大:输入不同频率的激光脉冲时,一开始便存在增益峰,随着输入功率的增加又出现一个新增益峰,然后逐渐合二为一,最后又一分为二;向外偏移的峰与最先出现的增益峰融合继而展宽变强,向内偏移的则缓慢增强展宽.输入激光频率相同时增益峰的强度宽度都较小,而且最外侧的增益峰和中间增益峰分离出的向外偏移的部分融合后并未持续展宽增强而是消失了,向内偏移的峰随着输入功率的增加,宽度和强度逐步加大,但远小于不同频率时向内偏移的增益峰.在反斯托克斯部分,两图同为双峰结构,但输入不同频率的激光脉冲时,随着输入功率的增大外侧增益峰加宽较为显著,其强度也强于内侧增益峰,输入相同频率的激光脉冲时,内侧明显强于外侧,两图反斯托克斯波的增益结构相同,变化趋势相近.

图4 反常色散区考虑拉曼效应,输入两束不同和相同频率激光脉冲时,增益随频率和功率的变化 (a)不同频率;(b)相同频率

当群速度失配为δ=1.9 ps/m,输入功率恒定为P=250 W时可得增益随波长差的变化关系如图5所示.

在反常色散区,增益随波长差的增加同样呈现出略微展宽和增强的特性,整体变化趋势也没有产生变化.

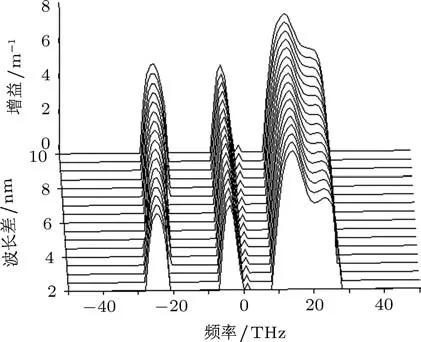
图5 反常色散区输入功率和群速度失配恒定时,增益随波长差的变化

图6 反常色散区考虑拉曼效应,输入两束不同和相同频率激光脉冲时,增益随频率和群速度失配常数的变化 (a)不同频率;(b)相同频率

输入功率恒定为P=250 W时增益随频率和群速度失配常数的变化关系如图6所示.从图6中可以看出,输入激光脉冲频率不相同时,斯托克斯和反斯托克斯部分的增益变化趋势与输入频率同时基本一致,只是增益峰的强度有所差异.输入激光脉冲频率不同时,斯托克斯部分起初只存在一个较相同频率小的增益峰,随着群速度失配的增加分离为两个增益峰,靠近中心频率处的强度宽度基本不变,另一部分强度比相同频率时强,且逐渐增强并向外侧远离中心频率方向偏移,最终和外侧新出现的增益峰融合,随着群速度失配的进一步增加,增益峰开始分离,内侧的部分与初始增益峰融合后迅速衰减并消失,另一分离出来的部分强度缓慢增强,向远离中心频率的外侧偏移,其强度明显强于相同频率的情况.在反斯托克斯部分起初存在一强度和宽度都大于斯托克斯部分的增益峰,但弱于同频率相对应的增益峰,随着群速度失配的增大,这个增益峰开始分离,在内侧出现一宽度和强度基本保持不变的增益峰,外侧的增益逐渐增强,强度明显大于同频率对应的增益峰,而且随着群速度失配的增加向外侧偏移.可以利用增益外侧远离中心频率分离特性提取太赫兹脉冲.

2.3 一个在正常色散区另一个在反常色散区

由于γx与γy相差不大,β21与β22的绝对值相差也不大,通过增益的表达式(9)式可以看出β21与β22在一正一负的情况下,不管哪个取正数对方程的影响都相同,所以当β21和β22一个处于正常色散区另一个反常色散区时,在不同色散区时可以得出增益随功率的变化关系图7.从图7中可以看出,不考虑拉曼效应时,斯托克斯部分和反斯托克斯部分互相对称,同为单峰结构,随功率增加而增强展宽的增益峰.考虑拉曼效应时,两边不再对称,在斯托克斯部分,在靠近中心频率的内侧当输入功率达到一定值会出现一新的增益峰,强度迅速增大,超过先出现的增益峰,当输入功率持续增大,两峰开始出现融合的趋势.在反斯托克斯部分,只存在一个同斯托克斯外侧的增益峰相同的逐渐增大展宽的增益峰.

群速度失配为δ=1.9 ps/m,输入功率恒定为P=250 W可以得出增益随波长差的变化关系如图8所示.

图8同图2、图5体现出相同的特性,在波长差增加时,增益峰有略微的展宽和增强,但整体趋势不变.

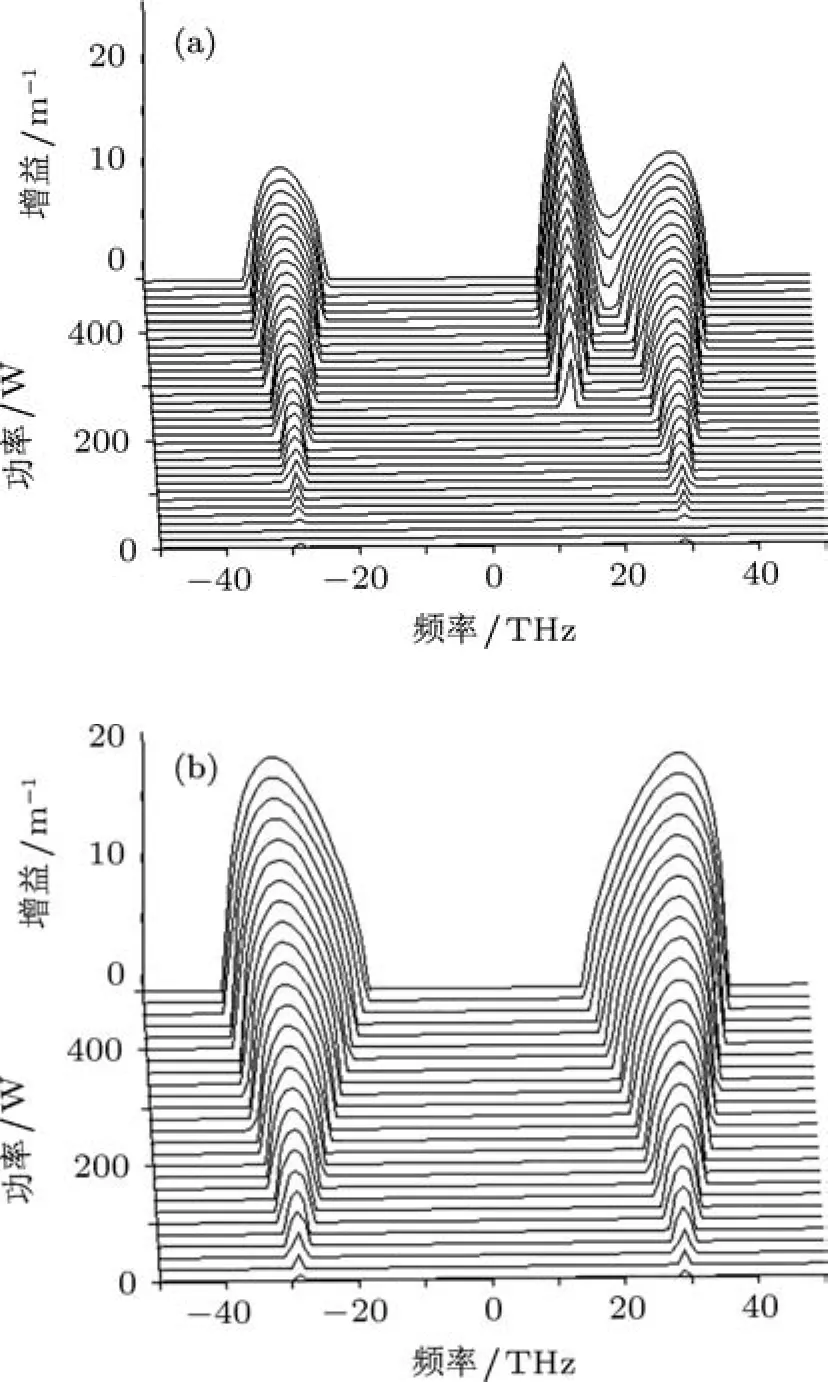
图7 β21与β22分别在正常和反常色散区时,考虑拉曼效应(a)和不考虑拉曼效应(b)时,增益随频率和功率的变化关系

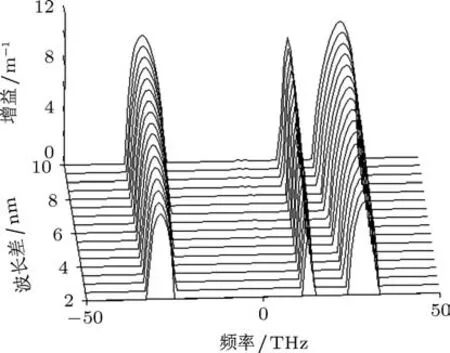
图8 不同色散区输入功率和群速度失配恒定时,增益随波长差的变化关系

当输入功率恒定为P=250 W时,增益随群速度失配常数的变化关系,如图9所示.不考虑拉曼效应时,左右两部分互相对称,开始在靠近中心频率附近存在一增益峰,随着群速度失配的增加增益峰的强度和宽度基本保持不变,只是向远离中心频率的方向偏移.考虑拉曼效应时左右不再对称.在斯托克斯部分,开始存在一个增益峰,其强度强于不考虑拉曼效应时的增益峰,随着群速度失配的增加,逐渐减小并分裂为两个增益峰,内侧的继续减小并最终消失,外侧的减小到一定程度后保持不变,持续向远离中心频率方向偏移,强度较不考虑拉曼效应时小.在反斯托克斯部分,开始存在两个增益峰,内侧的增益峰较大,且小于不考虑拉曼效应时的增益峰,随着群速失配的增加迅速减小消失,外侧的增益峰强度则随群速度失配的增大而缓慢增大,到一定强度时,趋于稳定不变,并不断向远离中心频率方向偏移,强度较不考虑拉曼效应时弱.

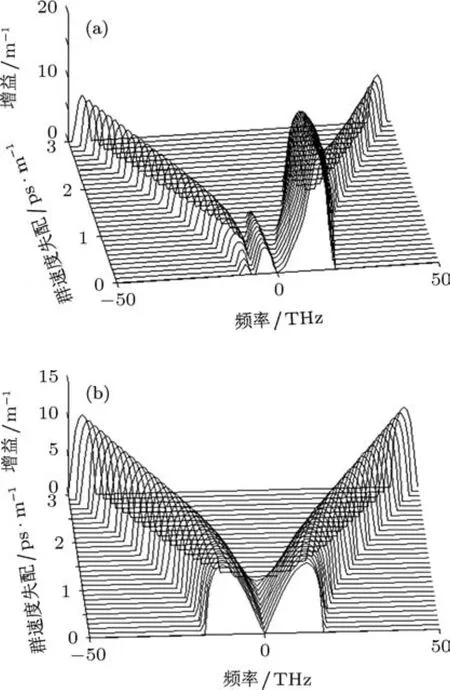
图9 β21与β22分别在正常和反常色散区时,考虑拉曼效应(a)和不考虑拉曼效应(b)时,增益随频率和群速度失配常数的变化

3 结论

沿双折射光纤两偏振轴输入不同频率的激光脉冲时,在同为正常色散区和反常色散区产生的增益谱与输入相同频率的激光脉冲时有很多相似之处,但又产生了明显区别.两种情况下增益谱的总体结构没有太大的变化,一般在相同的位置都有增益峰,而且增益峰的走势基本相同,靠近中心频率附近的增益峰强度差别较小,主要的区别在于外侧的增益峰.输入不同频率的激光脉冲时,所产生的增益峰强度明显更强宽度更宽,而且外侧的增益峰在输入功率较小时出现,而相同频率的状况下,一般在功率达到一定值时某些增益峰才会出现.当两个色散系数处于不同的色散区域时,通过与不考虑拉曼效应的情况的对比,发现考虑拉曼效应后,破坏了原本增益谱斯托克斯部分和反斯托克斯部分的对称性,增益谱结构发生明显的改变,且斯托克斯部分明显强于反斯托克斯部分.

[1]Qiu M 2001 Micro.Opt.Technol.Lett.30 327

[2]Liu X Y,Zhang F D,Zhang M 2007 Chin.Phys.B 16 1710

[3]Kim S,Kang J U 2004 IEEE Photonies Technol.Lett.16 494

[4]Ning T G,Qin X,Pei L,Tan Z W,Tong Z,Jian S S 2006 Chin.J.Laser 133 1078(in Chinese)[宁提纲,秦曦,裴丽,谭中伟,童治,简水生2006中国激光133 1078]

[5]Han K J,Lee Y W,Kwon J,Roh S,Jung J,Lee B 2004 IEEE Photonics Technol.Lett.16 2114

[6]Silva N A,Muga N J,Pinto A N 2009 J.Lightwave Technol.27 4979

[7]Lin Q,Agrawal G P 2006 Opt.Lett.31 3086

[8]Katsuragawa M,Hakuta K 2000 Opt.Lett.25 177

[9]Bi C Z,Wu Y J 2007 Infrared Laser Eng.36(supplement)566(in Chinese)[毕聪志,吴衍记2007红外与激光工程36(增刊)566]

[10]Gong Z B,Zhang S M 1992 J.Appl.Opt.13 40(in Chinese)[龚智炳,张栓民1992应用光学13 40]

[11]Jia W G,Qiao L R,Wang X Y,Yang J,Zhang J P,Meng K N M L 2012 Acta Phys.Sin.61 4215(in Chinese)[贾维国,乔丽荣,王旭颖,杨军,张俊萍,门克内木乐2012物理学报61 4215]

[12]Jia W G,Qiao L R,Wang X Y,Meng K N M L,Yang J,Zhang J P 2012 Acta Phys.Sin.61 4209(in Chinese)[贾维国,乔丽荣,王旭颖,门克内木乐,杨军,张俊萍2012物理学报61 4209]