基于体素相似性的三维多模脑图像配准研究

吕晓琪 LV Xiaoqi

李 娜 LI Na

张宝华 ZHANG Baohua

谷 宇 GU Yu

贾东征 JIA Dongzheng

内蒙古科技大学信息工程学院 内蒙古包头 014010

基于体素相似性的图像配准[1,2]，是用两图像对应体素对间的几何相似性搜索全局最优变换参数，避免了分割和特征提取的精度损失，并自动完成配准。目前，基于体素相似性的配准主要有3种：①基于灰度差异，速度快，但只适用于单模下灰度差异较小的图像间配准；②基于相关系数，要求对应体素的灰度值存在线性相关性，在多模配准中会出现误配；③基于信息论，以互信息为相似性测度，不依赖于图像数据关系的假设，对多模图像间的灰度关系也不用特殊假设，几乎可用于任何多模图像间配准[3]。因此，基于体素相似性的互信息算法广泛应用于多模图像配准中[4-7]。

常用的配准优化方法有单纯形法、Powell法、梯度下降法、模拟退火法、粒子群优化法、遗传算法等，其中前3种是局部优化算法，收敛速度快，但易陷入局部极值；后3种是全局优化算法，减少了陷入局部极值的概率，但计算量大，优化速度慢。

本研究用Mattes互信息作为相似性测度以实现三维多模脑图像配准。此测度函数通常是不光滑的，容易受局部极值的影响，导致误配准。这就要求一种策略能利用测度函数连续和可微的特性，得到一个接近全局最优的变换参数，并且计算速度快，还不影响配准的准确性。本研究详细分析了互信息算法和多分辨率金字塔算法的计算原理，并将其有效结合，通过平滑滤波在一定程度上避免了局部极值，提高了配准精度和鲁棒性，使用下采样减少了数据量，提高了配准速度。

1 三维医学图像的配准流程

1.1 三维配准体数据的常用格式和获得方法 三维配准体数据的常用格式有Analyze文件、NifTI-1文件和MetaImage文件，可以通过两种方式获得体数据：读取一系列二维切片构成一个三维体数据，最后将体数据写到指定文件中；利用医学图像转换应用程序包MRIConvert把二维 DICOM切片系列文件集转换成需要的三维体数据。

本研究选用的三维体数据格式是MetaImage文件，由raw二进制数据文件和mhd头文件构成，对三维图像的存取是通过头文件访问对应的数据文件。

1.2 三维配准的一般流程 实现三维医学图像配准需要以下基本模块：空间变换、配准测度、插值器和优化器。其中，配准测度是配准框架中最关键的部分，用于评估配准效果；插值器影响搜索空间的平滑度和整个配准的执行时间。

配准组件用来协调整体，以确保在传递给优化器之前准备工作都已完成。Observer/Command类对象用来监测优化器并跟踪配准迭代过程，判断优化器是否正常工作，振幅长度是否合理，不必等优化器自动停止即可中断配准程序调整初始化参数，这样就完成了整个配准算法过程（图1）。

图1 三维配准基本流程

2 基于互信息的配准方法

2.1 以互信息为相似性测度 互信息的主要优点是不需要指定其依靠的实际形式。因此，待配准的两幅图像之间的复杂映射能够模型化，这种灵活性使互信息很好地适应了多模配准的标准。本研究选择了Mattes等[8]提出的互信息方法作为相似性度量。

医学图像配准本质上是一个函数优化问题，即一系列变换参数μ最大化一个图像相似度函数S：

本研究用互信息作为图像的相似度函数，假设最大化相似度函数的这一组变换参数{μopt}能使变换后的浮动图像很好地对齐到参考图像上。公式（1）呈现的是最大化问题，但是Mattes互信息计算出负的交互信息，因此，实际上要最小化这个负的相似度函数S。假设LF和LR分别是浮动和参考图像的离散灰度集。参考和浮动图像之间的负互信息S表示为变换参数μ的函数如下：

其中，P、PF和PR分别是联合概率分布、浮动图像边缘概率分布和参考图像边缘概率分布，后面将会导出。

对于高维的空间变换参数，采用梯度准则有助于寻找其最大值。互信息的梯度公式如下：

单个的梯度通过公式（2）对变换参数μ求微分得到：

用于计算互信息的概率分布是基于参考和浮动图像的边缘和联合直方图。Parzen窗用来形成连续的基本图像直方图估计，也减少了插值量化和二进制数据离散化的影响。因此，联合概率分布是可微函数。用β（3）作为3次样条Parzen窗口，β（0）作为0次样条Parzen窗口，联合离散型概率分布如下：

浮动图像的边缘离散概率分布通过联合分布计算如下：

参考图像的边缘离散型概率分布可以独立于变换参数来计算，通过B样条Parzen窗来满足分区的联合约束。计算公式如下：

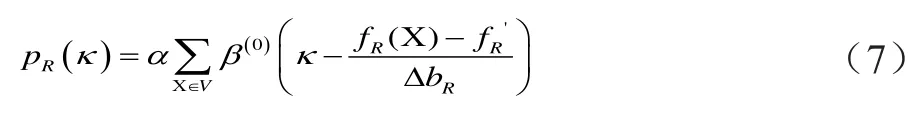
2.2 初始变换参数的估计 三维多模医学图像配准是使两幅待配准图像在同一空间坐标系中达到空间位置上的对齐，用Vr和Vf分别表示参考体和浮动体，两点（xr∈Vr，xf∈Vf）间的几何映射可以表示为：

其中，xr和xf分别表示来自体数据vr和vf的空间坐标的体素点，M是两点间的几何变换矩阵。本研究中的所有实验图像都来自脑部，头骨的刚性特性使得脑部被认为是刚性的，因此，刚性变换矩阵M由3个平移和3个旋转来定义，可以写成一个平移向量T(t)和一个旋转矩阵R连接的齐次坐标形式：

因此，矢量表示的刚体变换公式（8）可以重写为：

一个常见的描述旋转矩阵的方法是以分解形式表示的一系列矩阵：

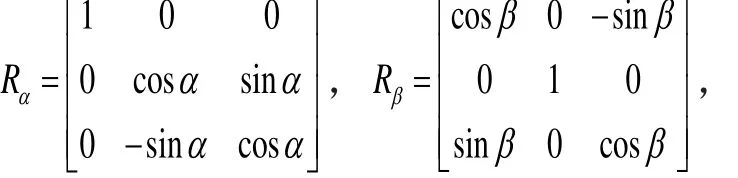
旋转矩阵可以分解为R=RγRβRα。定义一个解剖坐标系，以体图像的中心为原点，X轴方向定义从右到左，Y轴方向从前到后，Z轴方向从颅低到颅顶。Rα、Rβ和Rγ分别表示图像绕X轴、Y轴和Z轴正发生旋转。

因此，参考体vr和浮动体vf之间的相关位置由这样一组参数决定，其中，tx、ty和tz是平移量，α、β和γ分别是浮动体沿着相关的参考体三维轴旋转的角度。从而，为了使浮动体更好地对齐到参考体上，图像配准就转化为寻找最优参数组P的过程。

2.3 图像多分辨率策略 多分辨率配准框架需要一对图像金字塔来平滑和下采样图像[9-11]。高斯金字塔、小波变换、拉普拉斯金字塔和steerable金字塔等常用于医学图像配准。本研究使用的是高斯金字塔，其底层金字塔T0是原始图像，通过低通滤波和下采样获取下一个金字塔层次T1，然后T1以同样的方式滤波和下采样获得T2，重复以上步骤，生成剩下的金字塔层次结构。显然，这个金字塔结构是通过迭代得到的，迭代公式如下：

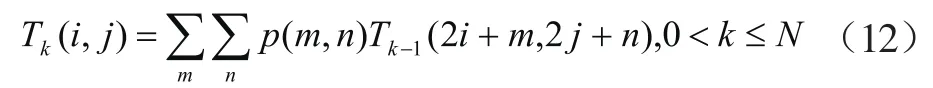
其中，Tk(i, j)表示第k层金字塔图像，i是图像的列数，j是图像的行数，k是金字塔的层数，p(m, n)是一个5×5的高斯模板窗口函数。

2.4 结合多分辨率的互信息配准 互信息配准函数通常是不光滑的，有多个局部最大值。局部最大值可能由以下原因引起：一部分局部最大值来自两幅待配准图像的局部对齐；另一部分来自配准算法执行过程，如插值算法或者图像重叠部分的变化等，这一部分是不合理的。面对庞大的三维体数据集，本研究把Mattes等提出的负互信息度量作为相似性测度的方法和多分辨率金字塔算法相结合。这种混合算法先将金字塔分解两幅待配准图像，得到分层次多分辨率的图像；接着对金字塔的粗糙尺度层进行参数的最优搜索，由于减小了图像尺寸，从而加快了收敛速度；然后将粗糙水平的搜索结果用来初始化下一层较细尺度的图像执行配准，该尺度层有了初始化估计，也加快了变换参数的搜索；最后重复以上过程，直到达到最细尺度层，得到最优的配准结果。此混合配准算法的大部分迭代过程是在粗尺度层上进行，并给出了初始化估计，因此，在细尺度层的配准迭代减少，加快了配准的收敛速度。

多分辨率策略是结合下采样和平滑操作的一种图像金字塔结构，通过由粗糙到平滑的方式解决配准问题。金字塔分解使平滑滤波后的图像尽量保留所需要的全局有用信息，在一定程度上减少了局部极值的影响，提高了配准的成功率、速度和鲁棒性。

3 实验结果与分析

为了验证本研究提出的算法对多模三维体图像的有效性，分别进行了三维单模和多模配准。采用3种算法进行对比分析：算法①用均方差[12]作为度量，算法②用Mattes互信息作为度量，算法③用加入了多分辨率金字塔算法的Mattes互信息作为度量，即本研究提出的算法。

本研究实验程序用VC++2005实现，配准程序中主要参数设置：收敛步长为0.0001，空间取样数量用大概像素的1%，平均信息数的二进制位数为64，最大迭代次数为500。

3.1 单模三维配准 选取来自BrainWeb网站的图像为实验对象。参考图像为质子密度（PD）加权的脑部MR体图像，体数据为181×217×180，沿每个方向像素之间的间隔均为1.0 mm；浮动图像在参考图像的基础上绕原点旋转20°，并在X轴方向上移动20 mm。

分别用上述3种算法对两幅待配准图像进行配准，由于从体图像显示上难以看出这3种算法的细微差别，所以仅对其中1种算法的配准输出进行显示来说明配准问题。结果发现，本研究提出的算法比前2种算法有更高的精确度，同时运行速度也得到了很大的提高（表1）。采用体三视图对比显示配准输出的结果发现，浮动体图像发生了很大的偏移和旋转，浮动体图像和参考体图像得到了很好的配准（图2）。

3.2 多模三维配准 选取美国Vanderbilt大学图像数据库中的Practice组脑图像数据进行多模三维配准，图像包括一个患者的CT图像数据、PET图像数据和不同成像参数（T1、T2、PD加权，几何失真校正的T1-rectif i ed、T2-rectif i ed、PD-rectif i ed）的MR图像数据。该组数据被研究人员用来完成算法的初步评估（表2）。这组图像提供了CT到MR、PET到MR配准的标准刚体变换数据，该变换数据给出了浮动体图像8个顶点的原始物理空间位置坐标和经过配准变换后的位置坐标。因此依据这组数据，采用8点评估标准对本研究提出算法的精确性进行评价。

表1 三种算法配准结果对比

图2 Mattes互信息算法单模配准前后对比，上排为横断面对比图，中排为矢状面对比图，下排为冠状面对比图。A~E分别为参考图、原始浮动图、配准后浮动图、配准前差别图、配准后差别图

表2 Practice组脑图像数据的大小和像素间隔

经验证，算法①进行多模配准时由于超过限定的迭代次数而溢出，配准失败，说明算法①只适合进行单模配准。因此，只用Mattes互信息法和改进后的混合算法对CT和MR体图像进行配准比较，MR作为参考体图像，CT作为浮动体图像。把经过配准变换后的CT浮动体图像的8个顶点的空间坐标qj,MR和标准的8个对应点qj,ref按公式（13）求平均几何距离△，用以评价配准结果：

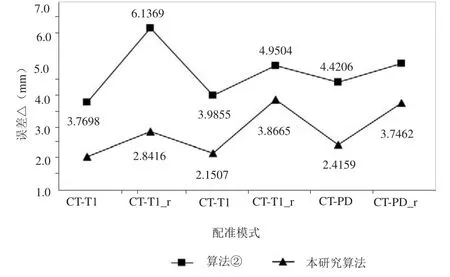
图3 CT到不同成像参数的MR图像配准误差

从图3可以看出，使用算法②的配准误差中，只有CT-T1和CT-T2配准模式误差小于一个像素大小，其余模式由于陷入局部极值等原因，造成配准结果出现误差，导致精度较低。然而加入多分辨率金字塔的Mattes互信息算法采用多步分解配准策略，在较低分辨率层次消除局部极值，从而提高了配准的精度，增强了配准的鲁棒性，所有配准误差都小于一个像素大小，可认为配准结果达到了亚像素级标准。

图4 本研究算法多模配准前后对比 ，上排为横断面对比图，中排为矢状面对比图，下排为冠状面对比图。A~E分别为最初CT浮动图、MR参考图、配准后CT图、配准前差别图、配准后差别图

采用横断面、矢状面、冠状面三视图分别对比显示CT到MR配准的结果。利用本研究算法可得到很好的配准结果（图4）。在相同实验条件下，由于算法②存在局部极值使配准精度比本研究提出的算法精度要低得多，仅用横断面显示算法②的配准结果（图5）。

通过图4可知，参考体与浮动体原始空间位置相差较大。对比横断面图4C和图5A、图4E和图5B可以得出，加入多分辨率金字塔的Mattes互信息算法使两幅体图像在空间位置上得到了很好的对准。

图5 Mattes互信息算法多模配准横断面输出图。A. 配准后CT图；B. 配准后差别图

4 结束语

基于体素相似性的Mattes互信息算法是利用不同模态下的图像灰度信息的统计特性来执行配准，不需要分割和特征提取，从而提高了配准的精度和鲁棒性，但是互信息配准函数通常是不光滑的，在插值或者图像重叠部分变化的过程中，容易陷入局部最优，导致配准的精度降低，甚至出现很大的误配。多分辨率金字塔算法采用分层的、由粗到精的递进搜索，可以配合互信息算法有效地避免在收敛过程中陷入局部极值的情况。实验证明，用这种混合配准算法对三维CT、MR图像进行多模配准，两幅待配准图像在空间位置上得到了很好的对齐，配准的精度达到了亚像素级。

[1] Nyúl LG, Udupa JK, Saha PK. Incorporating a measure of local scale in voxel-based 3-D image registration. IEEE Trans Med Imaging, 2003, 22(2): 228-237.

[2] Loeckx D, Maes F, Vandermeulen D, et al. Voxel based nonrigid image registration using local and partial volume similarity measures. Proceedings 7th IEEE international symposium on biomedical imaging, 2010: 348-351.

[3] Maes F, Collignon A, Vandermeulen D, et al. Multimodality image registration by maximization of mutual information.IEEE Trans Med Imaging, 1997, 16(2): 187-198.

[4] 余慧婷, 张杰, 潘萌. 噪声对三维图像归一化互信息配准的影响. 中国医学影像学杂志, 2011, 19(11): 844-849.

[5] 胡凯, 王卫东, 邱本胜, 等. 颅颌面CT与MR图像的配准.中国医学影像学杂志, 2002, 10(2): 123-125.

[6] 刘晴, 郭希娟, 许慎洋. 基于互信息的N维多模医学图像配准. 中国图象图形学报, 2009, 14(10): 2061-2068.

[7] Lee D, Hofmann M, Steinke F, et al. Learning similarity measure for multi-modal 3D image registration. IEEE Conference on CVPR. Tubingen: Germany, 2009: 186-193.

[8] Mattes D, Haynor DR, Vesselle H, et al. PET-CT image registration in the chest using free-form deformations. IEEE Trans Med Imaging, 2003, 22(1): 120-128.

[9] Thévenaz P, Unser M. Optimization of mutual information for multiresolution image registration. IEEE Trans Image Process,2000, 9(12): 2083-2099.

[10] 李乔亮, 汪国有, 刘建国, 等. 基于样条金字塔和互信息的快速图像配准. 计算机应用研究, 2009, 26(5): 1949-1950, 1960.

[11] Bunting P, Labrosse F, Lucas R. A multi-resolution area-based technique for automatic multi-modal image registration. Image Vis Comput, 2010, 28(8): 1203-1219.

[12] 谢小辉, 杨光, 那奇, 等. 肝脏介入治疗中基于B样条变形形变模型的配准. 中国医学影像学杂志, 2011, 19(8): 616-619.