带模糊参数的理想化模糊软环
2013-12-07刘先平
刘先平
(湖北民族学院 理学院,湖北 恩施 445000)
带模糊参数的理想化模糊软环
刘先平
(湖北民族学院 理学院,湖北 恩施 445000)
根据环的模糊理想和带模糊参数的模糊软集的概念提出带模糊参数的理想化模糊软环和带模糊参数的模糊软环同态的概念,讨论它们的基本性质.并进一步提出随模糊参数递增(递减)的理想化模糊软环的概念和相关理论.
模糊理想;理想化模糊软环;模糊软同态
美国控制论专家L.A.Zadeh于1965年提出模糊集概念[1],奠定了模糊理论的基础.模糊理论是处理不确定信息的一种数学方法.许多学者把模糊集应用到代数理论中,模糊代数理论得到了迅速发展.Rosenfeld 引入了模糊子群和模糊子半群的概念[2],Mukherjee引入了模糊子环和模糊理想的概念并进行了相关研究[3],其他学者也对其展开进一步研究,得到了许多重要结论.1999年Molodtov又提出软集的概念[4],它是一种新的处理不确定性、不精确性的数学工具.近年来,软代数理论也得到了快速的发展[5-10].Maji结合模糊集理论和软集理论提出了模糊软集的概念[11],Cagman进一步提出了带模糊参数的软集和带模糊参数的模糊软集的概念[12-13].本文根据环的模糊理想和带模糊参数的模糊软集的相关理论提出带模糊参数的理想化模糊软环的概念,讨论它们的基本性质.并进一步提出随模糊参数递增(递减)的理想化模糊软环的概念和相应理论.
1 预备知识
定义1[1]设μ是集合U到[0,1]的映射,即μ:U→[0,1],称映射称μ是U的一个模糊集,μ(x)称为模糊集μ的隶属函数,U的全体模糊集所构成的集合记为F(U).若μ,ν∈F(U),μ∪ν称为μ与ν的并,其中(μ∪ν)(x)=max{μ(x),ν(x)};μ∩ν称为μ与ν的交,其中(μ∩ν)(x)=min{μ(x),ν(x)}.
定义2[3]设R是一个环,μ是R的一个模糊集,若对∀x,y∈R,满足下列条件:
(1)μ(x-y)≥min{μ(x),μ(y)},
(2)μ(xy)≥max{μ(x),μ(y)},
则称μ是R的一个模糊理想.
定义3[11]设U是一个集合,E是一个参数集,如果γ为E到F(U)的一个映射,即γ:E→F(U),则称序对(γ,E)为集合U上的模糊软集.
定义4[13]设U是一个集合,E是一个参数集,X是参数集E的模糊集,其隶属函数记为μX(x),即μX:E→[0,1],γX为E到F(U)的一个带有模糊参数的映射,即γX:E→F(U),当μX(x)=0时,γX(x)=φ.称序对{(μX(x)/x,γX(x)):x∈E,γX(x)∈F(U),μX(x)∈[0,1]}为集合U上带模糊参数X的模糊软集,记为ΓX={(μX(x)/x,γX(x)):x∈E,γX(x)∈F(R),μX(x)∈[0,1]}.
定义5[13]设ΓX={(μX(x)/x,γX(x)):x∈E,γX(x)∈F(U),μX(x)∈[0,1]},ΓY={(μY(x)/x,γY(x)):x∈E,γY(x)∈F(U),μY(x)∈[0,1]}, 称ΓXΓY为ΓX与ΓY的交,其中ΓXΓY={((μX∩μY)(x)/x,(γX∩γY)(x)):x∈E};称ΓXΓY为ΓX与ΓY的并,其中ΓXΓY={((μX∪μY)(x)/x,(γX∪γY)(x)):x∈E}.
定义6[14]设X,Y是两个集合,f:X→Y是一个映射,μ,ν分别是X,Y的模糊集,则μ在f下的象和ν在f下的原象分别定义如下:
f-1(ν)(x)=ν(f(x)),x∈X.
引理1 设f是环R到环K的一个满同态,若μ是R的模糊理想,则f(μ)是K的模糊理想.
2 带模糊参数的理想化模糊软环
定义7 设R是一个环,E是一个参数集,X是E的模糊集,ΓX={(μX(x)/x,γX(x)):x∈E,γX(x)∈F(R),μX(x)∈[0,1]},如果对任意x∈E,γX(x)都是R的模糊理想,则称ΓX是R上带模糊参数X的理想化模糊软环.

E的模糊集X={0.2/a,0.6/b,0/c},


则ΓX={(μX(x)/x,γX(x)):x∈E}是R上带模糊参数X的理想化模糊软环.
定理1 设R是一个环,E是一个参数集,如果ΓX和ΓY分别是环R上带模糊参数X和Y的理想化模糊软环,则ΓXΓY是R上带模糊参数X∩Y的理想化模糊软环.
证明因为ΓXΓY={((μX∩μY)(x)/x,(γX∩γY)(x)):x∈E},ΓX和ΓY分别是环R上的带模糊参数X和Y的理想化模糊软环,即X,Y都是E的模糊集,且对∀x∈E,γX(x),γY(x)都是R的模糊理想.于是X∩Y也是E的模糊集,(γX∩γY)(x)也是R的模糊理想,即ΓXΓY是R上带模糊参数X∩Y的理想化模糊软环.
定理2 设R是一个环,E是一个参数集,如果ΓX和ΓY分别是环R上带模糊参数X和Y的理想化模糊软环,且X∩Y=φ,则ΓXΓY也是R上带模糊参数X∪Y的理想化模糊软环.
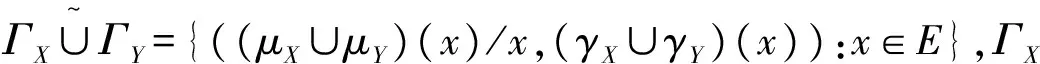
由引理1,容易得出下列结论:
定理3 设ΓX={(μX(x)/x,γX(x)):x∈E,γX(x)∈F(R),μX(x)∈[0,1]}是环R上的具有模糊参数X的理想化模糊软环,则ΓX={(μX(x)/x,f(γX(x))):x∈E}是环K上的具有模糊参数X的理想化模糊软环.
定义8 设R是一个环,A,B是两个参数集,X,Y分别是A,B的模糊集,ΓX={(μX(x)/x,γX(x)):x∈A,γX(x)∈F(R),μX(x)∈[0,1]},ΓY={(μY(x)/x,γY(x)):x∈B,γY(x)∈F(K),μY(x)∈[0,1]}
分别是环R,K上的具有模糊参数X,Y的理想化模糊软环,f是R到K的映射,即f:R→K,g是A到B的映射,g:A→B,如果满足下列条件:
1)f是R到K的满同态;
2)g是A到B的满射;
3)μX(x)=μY(g(x)),f(γX(x))=γY(g(x)),∀x∈A.
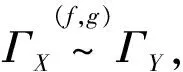
如果f是R到K的一个同构,g是一个双射,则我们称(f,g)是一个带模糊参数的模糊软环同构,称ΓX同构于ΓY,记为ΓX≃ΓY.
例2 设R=Z(+,×),K=3Z(+,×),A={1,2},B={2,4},f:R→K定义为f(r)=3r,g:A→B定义为g(x)=2x,A的模糊集定义为X={0.2/1,0.6/2,},B的模糊集定义为Y={0.2/2,0.6/4,},γX,γY分别定义如下:
;
显然,ΓX={(μX(x)/x,γX(x)):x∈A}和ΓY={(μY(x)/x,γY(x)):x∈B}分别是环R和K上的具有模糊参数X和Y的理想化模糊软环.我们可以验证,f是R到K的同构,g是A到B的双射,对∀x∈A,μX(x)=μY(g(x)),f(γX(x))=γY(g(x)),因此,ΓX同构于ΓY.
定理4 设ΓX={(μX(x)/x,γX(x)):x∈A,γX(x)∈F(R),μX(x)∈[0,1]}是环R上的具有模糊参数X的理想化模糊软环,ΓY={(μY(x)/x,γY(x)):x∈B,γY(x)∈F(K),μY(x)∈[0,1]}是环K上的具有模糊参数Y的模糊软集,如果ΓX~ΓY,则ΓY环K上的具有模糊参数Y的理想化模糊软环.
证明设(f,g)是从ΓX到ΓY的带模糊参数的模糊软环同态,由于ΓX是环R上的带模糊参数X的理想化模糊软环,即对x∈A,μX(x)∈[0,1],γX(x)是环R的一模糊理想;则对∀y∈B,∃x∈A,,使得g(x)=y,μY(y)=μY(g(x))=μX(x)∈[0,1],是环K的模糊理想,所以ΓY环K上的带模糊参数Y的理想化模糊软环.
3 随模糊参数递增(递减)的理想化模糊软环
定义9 设ΓX={(μX(x)/x,γX(x)):x∈E,γX(x)∈F(R),μX(x)∈[0,1]}是环R上的带模糊参数X的理想化模糊软环,对于∀x,y∈E,如果μX(x)≤μX(y),有γX(x)⊆γX(y)(γX(x)⊇γX(y)),则称ΓX是环R上随模糊参数X递增(递减)的理想化模糊软环.

E的模糊集X={0.8/a,0.6/b,0.1/c,0.4/d},
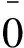
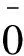
则ΓX={(μX(x)/x,γX(x)):x∈E}是R上随模糊参数X递增的理想化模糊软环.
注意,如果ΓX={(μX(x)/x,γX(x)):x∈E,γX(x)∈F(R),μX(x)∈[0,1]}和ΓY={(μY(x)/x,γY(x)):x∈E,γY(x)∈F(R),μY(x)∈[0,1]}分别是R上随模糊参数X和Y递增(递减)的理想化模糊软环,但ΓXΓY不一定是R上随模糊参数X∩Y递增(递减)的理想化模糊软环.

X={0.5/x1,0.4/x2},
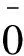
Y={0.1/x1,0.9/x2},
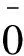
ΓX,ΓY分别是R上随模糊参数X和Y递增的理想化模糊软环,但是,X∩Y={0.1/x1,0.4/x2},
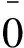
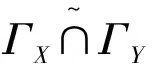
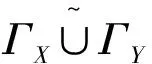

X={0/x1,0.4/x2},
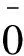
Y={0.1/x1,0/x2},
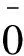
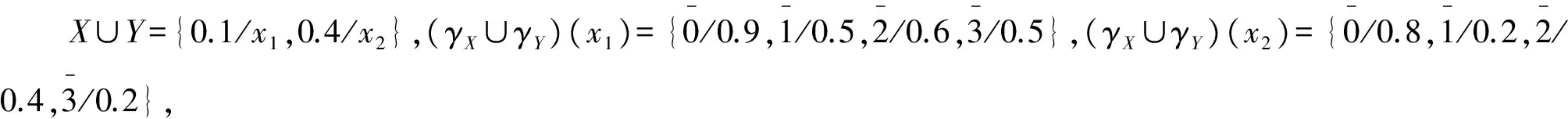
定理4 设ΓX={(μX(x)/x,γX(x)):x∈A,γX(x)∈F(R),μX(x)∈[0,1]}是环R上随模糊参数X递增(递减)的理想化模糊软环,ΓY={(μY(x)/x,γY(x)):x∈B,γY(x)∈F(K),μY(x)∈[0,1]}是环K上的带模糊参数Y的模糊软集,如果ΓX~ΓY,则ΓY环K上随模糊参数Y递增(递减)的理想化模糊软环.
证明设(f,g)是从ΓX到ΓY的带模糊参数的模糊软环同态,由于ΓX是环R随模糊参数X递增的理想化模糊软环,即对x1,x2∈A,μX(x1)≤μX(x2),γX(x1),γX(x2)是环R的模糊理想,且γX(x1)⊆γX(x2);对∀y1,y2∈B,若μY(y1)≤μY(y2),∃x1,x2∈A,,使得g(x1)=y1,g(x2)=y2.由于μY(y1)=μY(g(x1))=μX(x1),μY(y2)=μY(g(x2))=μX(x2),因此,μX(x1)≤μX(x2),γX(x1)⊆γX(x2),
γY(y1)=γY(g(x1))=f(γX(x1))⊆f(γX)(x2)=γY(g(x2))=γY(y2).
所以ΓY是环K上随模糊参数Y递增的理想化模糊软环.
对于ΓX是环R随模糊参数递减的理想化模糊软环的情形,同样可以证明ΓY是环K上随模糊参数递减的理想化模糊软环.
[1] Zadeh L A.Fuzzy sets[J]. Inform Control,1965,8:338-353.
[2] Rosenfeld A. Fuzzy groups [J].J Math Anal Appl,1971,35:512-517.
[3] Mukherjee T K, Sen M K. On Fuzzy ideals of a ring I [J].Fuzzy Sets and Systems,1987,21:99-104.
[4] Molodstov D. Soft set theory-first results [J].Comput Math Appl,1999,37:19-31.
[5] Aktas H, Cagman N. Soft sets and soft groups [J].Inform Sci,2007,177:2726-2735.
[6] Feng F.Soft semirings[J].Computers and Mathematics with Applications,2008,56:2621-2628.
[7] Jun Y B.Soft BCK/BCI-algebras[J].Comput Math Appl,2008,56:1408-1413.
[8] Jun Y B,Park C H.Applications of soft sets in ideal theory of BCK/BCI-algebras[J].Inform Sci,2008,178:2466-2475.
[9] Liu X P,Xiang D J,Zhan J M,et al.Isomorphism theorems for soft rings[J].Algebra Colloquium,2012,19:391-397.
[10] Liu X P,Xiang D J,Zhan J M.Fuzzy isomorphism theorems of soft rings[J].Neural Comput Appl,2012,21:391-397.
[11] Maji P K,Biswas R,Roy A R.Fuzzy soft sets[J].Fuzzy Math,2001,9:589-602.
[12] Cagman N,Citak F,Enginogglu S.FP-soft sets and its applications [J].Annals of Fuzzy Mathematics and Informatics,2011,2:219-226.
[13] Cagman N,Citak F,Enginogglu S.Fuzzy parameterized fuzzy soft set theory and its applications[J].Turkish Journal of Fuzzy Systems,2010,1:21-35.
[14] Liu Y,Liu S.Fuzzy isomorphism theorems of groups[J].Far East J Appl Math,2004,16:77-89.
IdealisticFuzzySoftRingswithFuzzyParameters
LIU Xian-ping
(School of Science,Hubei University for Nationalities,Enshi 445000,China)
The concepts of fuzzy parameterized idealistic fuzzy soft rings and fuzzy soft homomorphism are introduced based on fuzzy ideals and fuzzy parameterized fuzzy soft sets. Then some properties of them are given. Furthermore,idealistic fuzzy soft rings with increasing (decreasing) fuzzy parameters are proposed and corresponding properties are studied.
fuzzy ideals;idealistic fuzzy soft rings;fuzzy soft homomorphism
2013-03-29.
国家自然科学基金项目(61175055);湖北省教育厅自然科学研究项目(B20122904).
刘先平(1979- ),女,讲师,硕士,主要从事代数学研究.
0153.3
A
1008-8423(2013)02-0167-04
