动力调谐陀螺仪模型快速开环辨识

杨 光，李醒飞，孙 建，赵建远

(天津大学精密测试技术及仪器国家重点实验室，天津 300072）

动力调谐陀螺仪是一种工作于闭环状态的角速率测量元件．因其内部结构复杂，批量生产难以保证其传递函数模型参数一致，同时，这些参数还会因内部机械磨损、应力配合等因素发生改变．为了实时调整回路参数，保证闭环伺服性能，需要对动力调谐陀螺仪传递函数参数模型进行快速辨识，为陀螺仪伺服回路设计调整提供依据[1]．

目前关于动力调谐陀螺仪传递函数模型辨识的研究多使用正弦扫频信号作为激励信号，逐点检测系统对不同频率正弦信号的响应，获取系统频率特性曲线，并通过最小二乘拟合、傅里叶变换等方法得到频率响应函数[2]．该方案具有稳定、可靠等优点，但测试速度较慢，另外在开环测试中，输入信号幅度受对象特性限制，因而信噪比低，影响辨识精度．激励信号的选择在系统传递函数模型辨识中起着重要作用，包括信号类型、阶次等参数的确定．n 阶系统开环可辨识条件是激励信号满足2n 阶持续激励条件[3]，以充分激发出系统的所有模态．Callafon 等[4]的研究表明激励信号频率段应大于对系统所感兴趣的频率段．Pintelon 等[5]指出周期信号的激励可以简化辨识算法．采用多正弦信号作为激励信号兼具上述特点，可以一次性激励系统在各个频率上的特征[6]，相比扫频信号效率更高．同时，与最小二乘法相比，基于外加输入自回归(auto regressive exogenous，ARX)模型采用预报误差法进行模型参数估计可以简化辨识过程，降低参数估计误差、提高抑制噪声能力[7-9]．

笔者使用多正弦信号作为激励，对信号带宽、幅值进行选择，获得适宜于惯性元件测试的激励信号．在此基础上建立动力调谐陀螺仪模型辨识平台，获得实验数据，并基于ARX 模型采用预报误差法进行陀螺参数模型辨识．最后对辨识得到的模型进行了有效性验证．

1 动力调谐陀螺仪模型

典型的两自由度动力调谐陀螺仪由陀螺马达及悬挂在挠性支撑上的转子飞轮、信号器和力矩器等组成．在调谐状态下，其传递函数模型结构如图1 所示．图中：J 为陀螺转动惯量；H 为陀螺角动量；KT和KP分别为力矩器和信号器增益系数；Φx、Φy分别为陀螺仪壳体相对惯性空间的运动转角在陀螺仪壳体坐标系Oxyz 的Ox 和Oy 轴上的分量；α、β分别为陀螺仪转子相对壳体偏角在壳体坐标系Oy 和Ox 轴上的分量；Mx、My分别为作用于转子上的外力矩M在陀螺仪壳体坐标系Ox 和Oy 轴上的分量．令Φx= Φy= 0，动力调谐陀螺仪开环传递函数矩阵可以表示为

图1 动力调谐陀螺仪参考模型Fig.1 Reference model of DTG

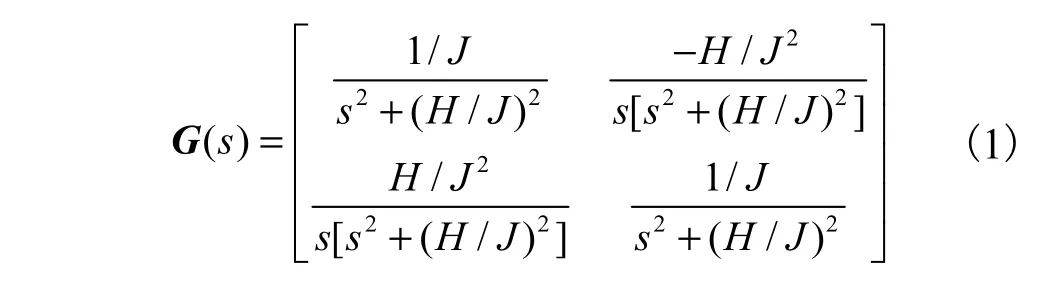
通过对力矩器施加激励信号，检测信号器输出响应，可以对系统参数模型进行辨识．

2 模型辨识

辨识过程需要考虑输入输出数据、模型类和辨识准则3 方面的内容[3]．首先进行辨识激励信号的设计，即如何设计辨识实验获取辨识数据．

2.1 辨识激励信号设计

本文采用多正弦信号作为动力调谐陀螺仪模型辨识的激励信号，其时域表达式为

式中：ia 为正弦量的幅值；0f 为起始频率；fΔ 为频率间隔；iφ为初相角，按线性分布．

可以看出，多正弦信号具有周期性、带宽和频谱可以任意精确设定以及无杂散频率成分等优点．另外，当初始相角按线性分布时，信号可以获得较低的峰值因子[6]，这样既可以增加输入信号幅度，提高信噪比，又能保证激励平稳均匀，适宜于惯性器件的参数辨识．

另外，通过对动力调谐陀螺仪工作频带进行加权可以更充分地激发出对象的动态特性．综上所述，对应激励信号时域表达式为

式中p 为对应工作频带ωn1～ωn2的加权．

2.2 基于渐进理论的模型辨识

确定辨识信号，并通过辨识实验获取输入输出数据后，下面需要选择模型类，并按照相应的辨识准则进行参数估计，得到系统模型估计ˆ(j) Gω．系统辨识渐进定理指出：当系统辨识模型阶数n 和数据样本数N 趋于无穷时，估计模型渐进收敛于真实模型．对于开环实验，模型估计方差[10-11]为

式中Φu和Φv分别为系统输入信号和噪声信号的功率谱密度．

由式(4)可知：①模型估计方差与输入信号功率谱相关，因此在选取激励信号加权值p 时，要保证尽可能大幅度激励对象的工作频段，以提高模型估计的准确性．②只要能保证足够的样本数据和模型阶次，模型的估计值将渐近收敛于模型的真实描述．即模型估计的渐近特性与模型结构没有关系，所以在选取模型类时选择结构简单的ARX 模型．

描述动力调谐陀螺仪模型的ARX 模型类可表示为

式中：u(t)、y (t)分别为激励信号、响应信号；Gij(q)为动力调谐陀螺仪子模型，i 和j 分别表示输出通道和输入通道序号．

子模型的ARX 模型结构为

对应差分方程可以描述为

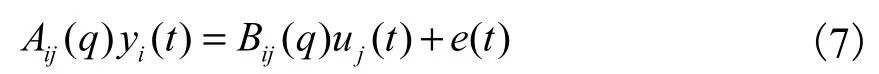
模型参数估计采用预报误差法，该方法不需要数据概率分布的先验知识，直接极小化预报误差准则函数即可．模型阶的确定采用赤池信息准则(AIC)[3]，模型的有效性检验采用计算模型预测输出与实验数据拟合度的方案．另外，由于动力调谐陀螺仪自身结构及加工装配工艺限制，系统测试数据会包含马达转频干扰以及陀螺电源频率干扰等，可以通过数据处理滤除．

3 实验及结果分析

为验证实际系统测试效果，以某型号动力调谐陀螺仪为辨识对象进行参数模型辨识测试．选用NI采集卡PCI-6251 对动力调谐陀螺仪施加激励并采集响应数据，上位机用于对数据进行处理和模型辨识．实验系统如图2 所示．

实验以交叉轴传递函数辨识为例(Gij(s)，i = 2,j= 1)，将多正弦信号作为输入信号，正弦量幅值300,mV，起始频率f0＝1,Hz，频率间隔Δf＝1,Hz，终止频率600,Hz，共600 个正弦波叠加，为了保证响应的稳定性，持续激励20,s．

图2 动力调谐陀螺仪模型测试系统Fig.2 Model testing system of DTG

根据本文的辨识方法，得到系统ARX 模型为

将以上辨识结果转换为连续传递函数，进而得到系统频率特性曲线，如图3(a)所示，可以看出，频率特性主要包括3 个峰值，其中455,Hz 是反映系统动态特性的章动频率，250,Hz 和500,Hz 分别为陀螺转子转频干扰以及陀螺电源频率干扰，并非系统对激励信号的响应，因此对响应数据中的干扰频率进行滤波处理，保留反映系统主要动态性的信息，重新进行模型辨识，得到辨识结果为

同上，可以转换得到动力调谐陀螺仪交叉轴频率特性曲线如图3(b)所示．

按照上面测试方法进行5 组重复实验，拟合结果修正取平均，化简可得到交叉轴的传递函数模型为

由式(10)可以得到参量H 和J 的实测值：H = 0.024 kg· m2· rad/s ，J = 8.4 ×1 0−6kg· m2．这与设计和生产参考值 H0= 0.025 kg· m2· rad/s ，J0=8.8 ×10−6kg· m2具有一致性，验证了设计指标．

图3 多正弦激励辨识结果Fig.3 Identification results got by the motivation of multisine

同时，为了进一步验证模型的可靠性，将基于该辨识模型获得的仿真输出与实验数据进行对比，结果如图4 所示，两组数据拟合度为95.3%，辨识得到的模型足以描述系统主要动态特性，满足控制器设计的需求．

图4 辨识模型的仿真输出与验证数据的比较Fig.4 Comparison between validation data and simulation output of identification model

最后，使用传统的系统扫频测试与本方案进行对比验证，同样选择频段1～600,Hz，进行多次重复性实验．为防止转子偏摆过大，扫频测试信号幅值定为60,mV．激励时间与前面保持一致，每个频率持续激励20,s，共测试100 个频率点．辨识结果如图5 所示，可以看到扫频得到的结果与按本文方案辨识得到的结果具有一致性．

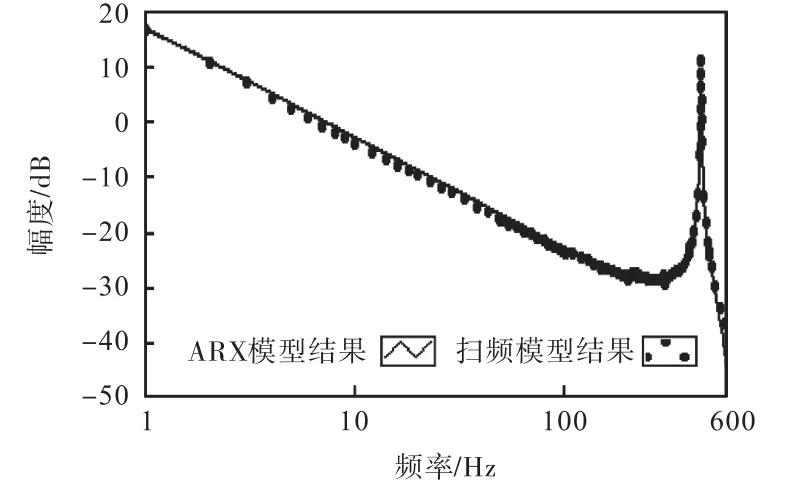
图5 ARX模型辨识与扫频得到交轴频率特性比较Fig.5 Comparison of the cross-axis frequency characteristic got by sweep and the ARX model identification

将两种方案进行对比，结果如表1所示．由表1 可以看出多正弦信号激励测试时间约20,s，而传统扫频法辨识却需要2,000,s．可见，由于多正弦信号可以在短时间内对系统工作频段给予充分激励，因而采用该方案可极大提高辨识效率．另外，多正弦信号输入激励均匀，保证陀螺转子不会超出限定的工作区间，因而激励幅值远高于扫频信号，同等条件下提高了输入信噪比，获得相对较高的模型拟合度.

表1 模型辨识方案比较Tab.1 Comparison of model identification program

4 结 语

实验结果表明，与扫频辨识方案相比，采用本文辨识方案，辨识效率得到大幅提高，测试时间由2,000,s 缩短为20,s；进一步改善辨识精度，模型对数据的拟合度由92.5%提高到95.3%；此外，本辨识方案大幅度提高了输入信噪比．为快速辨识动力调谐陀螺仪的参数模型并进行伺服回路优化设计，保证闭环伺服性能提供了可靠保证．同时，本方案也适用于液浮陀螺、石英挠性加速度计等惯性元件的传递函数测试建模．

［1］万健如，张建松，陈 超，等. 垂直陀螺180°回转伺服变结构 PID 控制[J]. 天津大学学报， 2006 ，39(8)：913-917.Wan Jianru，Zhang Jiansong，Chen Chao，et al. Variable PID control method for 180° back swing serve control system of vertical gyro[J]. Journal of Tianjin University，2006，39(8)：913-917(in Chinese).

［2］张连超， 范世 珣，范大鹏，等. 动力调谐陀螺再平衡回路数字化的研究与实现[J]. 光学精密工程，2007，15(12)：1974-1981.Zhang Lianchao，Fan Shixun，Fan Dapeng，et al. Research and implementation of digital control of dynamically tuned gyroscope rebalance loop[J]. Opt Precision Eng，2007，15(12)：1974-1981(in Chinese).

［3］Ljung L. System Identification：Theory for the User[M].2nd ed. NJ，Upper Saddle River：Prentice-Hall，1999.

［4］de Callafon R A，Van den Hof P M J. Multivariable feedback relevant system identification of a wafer stepper system[J]. IEEE Transactions on Control Systems Technology，2001，9(2)：381-390.

［5］Pintelon R，Vandersteen G，Locht L D. Experimental characterization of operational amplifiers ： A system identification approach(Part I)：Theory and simulations[J]. IEEE Transactions on Instrumentation and Measurement，2004，53(3)：854-862.

［6］侯国屏，吴 静，董甲瑞. Multitone 信号及其在测量中的应用[J]. 清华大学学报： 自然科学版，2007(10)：1574-1577.Hou Guoping，Wu Jing，Dong Jiarui. Multitone signals and its applications in measurement [J]. Journal of Tsinghua University：Science and Technology，2007(10)：1574-1577(in Chinese).

［7］Yang M，Makis V. ARX model-based gearbox fault detection and localization under varying load conditions[J]. Journal of Sound and Vibration，2010，329(24)：5209-5221.

［8］Karny M，Pavelkova L. Projection-based Bayesian recursive estimation of ARX model with uniform innovations[J]. Systems and Control Letters ， 2007 ， 56(9/10)：646-655.

［9］Li H，Wang D，Chen Z. Adaptive Hammerstein predistorter using the recursive prediction error method[J].Tsinghua Science and Technology，2008，13(1)：17-22.

［10］Ljung L. Asymptotic variance expressions for identified black-box transfer function models[J]. IEEE Transactions on Automatic Control，1985，30(9)：834-844.

［11］Zhu Y C. Multivariable System Identification for Process Control[M]. Netherlands：Elsevier Science Ltd，2001.