基于曲率图的三维点云数据配准

葛宝臻 ，彭 博 ，田庆国

(1. 天津大学精密仪器与光电子工程学院，天津 300072；2. 光电信息技术教育部重点实验室，天津 300072)

三维点云数据的配准与融合是计算机视觉领域一个基本而重要的问题．其研究成果在医学、逆向工程、虚拟现实、计算机视觉等领域得到了广泛的应用[1]．根据不同视图点云数据间是否存在畸变，现有的配准算法大致可以分为基于刚性变换的配准和非刚性配准两类．本文只讨论基于刚性变换的配准算法．给定具有重叠部分的三维点云数据，其任务是求取点云数据间的最佳刚性变换，使不同视图的点云数据准确地融合在一起[2-4]．

迭代最近点(iterative closest point，ICP)算法[5]是当前最流行的刚性配准算法，该算法以相对位置经过粗略配准的两片点云数据为基础，迭代求取两片点云数据间的对应点及相应的刚性变换，直到对应点之间的距离误差评价函数最小．该算法根据两点云数据点之间的距离来确定对应点，所以需要待配准的两点云数据之间基本已经配准．实际上待配准的点云数据间的相对位置往往未知，怎样利用粗略配准算法将点云数据间的相对位置变换到ICP 算法的收敛域成为问题的关键．

目前普遍的解决方法是通过不依赖于三维旋转和平移变换的点云特征信息来建立点云数据间的对应关系．这些特征信息包括法向[6]、曲率[7]、体积分[8]等简单的一维特征描述函数，还包括旋转图像[9]、形状内容[10]等高维特征描述函数，有的甚至还包括颜色、强度值等辅助信息．但存在的问题是，低维特征描述函数计算简单，但所包含的特征信息较少，且对噪声敏感；高维特征函数能很好地反映特征信息，但计算复杂，时间、空间开销较大，且怎样合理地进行特征比较是一个难题．

笔者致力于通过新颖的特征信息和匹配算法快速、准确地得到点云数据间的对应关系．受Gatzke等[11]的启发，在以点几何表示的三维点云数据中引入曲率图的概念，并将其作为三维点云数据的特征描述函数．该描述函数的优点在于通过选择不同的环数及各环半径值可得到不同的曲率图，很容易实现多比例空间的特征保持分析．有了曲率图的概念以后，本文的主要算法思想是通过一维曲率图粗选特征点和潜在对应点，然后对特征点和潜在对应点进行高维曲率图计算，并再次通过高维曲率图进一步精简潜在对应点．这样既保证了丰富的特征信息以获得正确的对应点，也大大减小了由于对整片点云进行高维曲率图计算所花费的时间和空间开销．在特征点的匹配算法上，对已有的Mitra 贪婪算法[12]进行了改进，大大提高了其稳定性．最后通过对真实三维点云数据进行配准，验证了该算法的有效性．

1 三维点云数据的曲率及曲率图

在微分几何中，对于三维欧几里得空间中可微曲面上的任一点A，给定了两个主曲率 1k 、2k[13]来衡量该点在不同方向上的弯曲程度．三维点云数据是对真实物体表面进行扫描采样获得的离散数据，点云数据中的每个顶点同样具有主曲率，不但如此，它还是点云数据的一项重要特性．经常提及和主曲率相关的几个曲率概念还有高斯曲率 K = k1k2、均值曲率

对于三维点云数据，估算其顶点主曲率 1k 、2k 的方法有很多，具代表性的有多项式拟合(polynomial fitting)法[15]、主成分分析(principal component analysis)法[16]以及移动最小二乘(moving least-squares)法[17]等．其中多项式拟合法对噪声敏感程度最小，稳定性高，但计算相对复杂；主成分分析法求解过程相对简单，但只适用于采样点稠密的大型点云；移动最小二乘法具有较好的法向估算精度，但需要求解非线性方程．本文根据不同的点云数据采取与之相适合的主曲率估算方法．但仅利用单一点的均方根曲率C 并不能很好地反映该点周围点的特征，并且对噪声比较敏感．曲率图利用该点及其周围点的曲率信息分布，能够准确地反映特征信息的同时有效地抑制噪声．下面分别介绍以点几何表示的三维点云数据中一维曲率图和高维曲率图的构造方式．这里以降采样后的点云数据Stanford bunny00[18]为例，对其表面上的任意一顶点A，一维曲率图的构造比较简单，如图1(a)所示，以目标点A 为球心，对半径为R 的球体内所有顶点的均方根曲率 Ci进行平均，得到的平均值即为该点的一维曲率图．

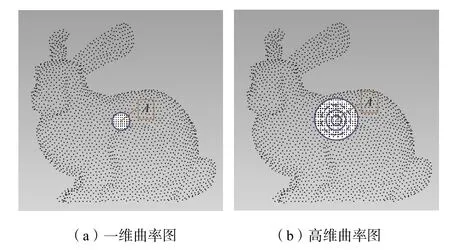
图1 曲率图的概念示意Fig.1 Sketch of curvature map

式中n 为距离A 点的距离小于R 的顶点个数．对于高维曲率图，如图1(b)所示，同样以目标点A 为球心，利用半径为 rj(0 ＜ j ≤m)的同心球将邻域空间划分为m 个球壳层，然后对每个球壳内的所有顶点的均方根曲率进行平均得到 f(rj)(0＜ j≤m)，高维曲率图 kmap即为 f(rj)随 rj的变化关系．用向量表示为

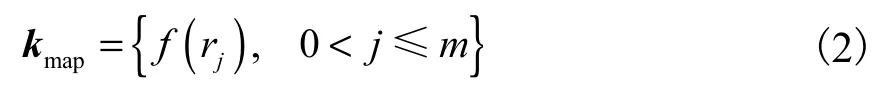
2 基于一维曲率图提取特征点

有了曲率图的概念以后，对三维点云数据的每个顶点进行一维曲率图运算．根据所有顶点的一维曲率图分布情况进行特征点的提取．这里采用的思想是对所有顶点的一维曲率图进行统计分析，求取一维曲率图的平均值μ和方差σ，选取一维曲率图 f(R)处于μ± kσ之外的点作为特征点．一片点云的数据量很大，使得一维曲率图往往近似服从正太分布，实验中发现 k = 1时，获得的特征点数量大致为点云总数的10%，通过调整系数k 可选择不同程度的特征点．为了使选取的特征点能更好地反映点云的特征信息，抑制噪声，对每个顶点选取不同的邻域范围做多比例空间的特征分析．这里通过改变一维曲率图的构造半径R ，例如对于半径为 Ri和 Ri+1时的邻域范围分别做特征分析得到特征点集 Pi和 Pi+1，选取 Pi和Pi+1的交集作为特征点．最后的特征点集为

式中n 为做多比例空间特征分析选取的半径个数．对Stanford bunny00 进行了基于一维曲率图的特征点提取及特征保持分析．算法流程为：采用空间包围盒法将三维点云数据结构化；在此基础上按欧式距离进行点云的K 邻域搜索；采用主成分分析法估算主曲率及均方根曲率(K＝20)；对每个半径R 分别计算每个顶点的一维曲率图 f(R)(R ＝0.000 5、0.001、0.002、0.005,mm)；对每个半径R 分别进行曲率图统计分析，选取 f(R)处于μ± kσ之外的点作为该曲率图半径下的特征点集(k ＝1)；对上述4 个曲率图半径R进行多比例空间的特征保持分析，得到特征保持点集；对特征保持点集按一定间隔距离值(0.005,mm)进行采样．

图2所示为该算法的特征点提取过程．图2(a)为R ＝0.000 5,mm 时提取到的特征点，可以看到，通过一维曲率图提取到的特征点基本上都是处在兔子的耳朵、脖子、腿等轮廓特征比较明显的部位，验证了一维曲率图提取特征点的有效性；图2(b)显示了通过多比例空间的特征保持分析后得到的特征保持点集，对比图2(a)可知，特征保持分析能有效去除一些非特征点或特征不够显著的点；图 2(c)为按0.005,mm 间隔对特征保持点集采样的结果，对特征保持点集按一定距离采样是为了进一步减少特征点数量，且让特征点间有一定的距离，为后面的配准算法打下了基础．

图2 特征点的提取过程Fig.2 Process of extracting feature points

3 高维曲率图精简潜在对应点

对于要配准的两片点云数据，通常称之为源点集和目标点集．理论上，只要在源点集和目标点集之间至少找出3 对对应点，就能够计算出这两片点云数据间的刚性变换关系，从而将这两片点云数据配准到一起．因此，准确找到点集间的对应点成为配准的关键．

本文的思想是对源点集进行基于一维曲率图的特征点提取，然后对目标点集进行相应的一维曲率图运算，一维曲率图半径为R ．对源点集中的每个特征点根据半径为R 时一维曲率图的相似性在目标点集中求取相应的对应点，即选取 fp(R) − fq(R )≤Δ的点作为该特征点的潜在对应点，Δ为设定阈值，设定原则是保证理论上具有对应点的特征点都能在潜在对应点中找到正确的对应点．通过实验发现，该值设为所有源点集中特征点的一维曲率图平均值的10%时，基本能够满足上述要求．此时源点集中的一点 pi往往对应目标点集中的多个点 qi1，qi2，…，qik．为进一步减少潜在对应点的数量，有效去除错误对应点，对pi及其潜在对应点 qi1，qi2，…，qik进行高维曲率图运算，高维曲率图的半径大小及环数根据点云采样密度决定．然后将 pi的高维曲率图分别与 qi1，qi2，…，qik的高维曲率图做比较，比较的方式直接采用高维空间的欧式距离，即E2中选择与 ie 没有交集的2 点对 je ，使得 ie 、je 组成的4 点对的距离均方差dRMS 最小．每构成一个新的4 点对，便从E2中删除包含这4 点对中任意一点的2 点对，遍历直到E2为空．最后得到4 点对集E4，同样按照距离均方差的值对E4升序排列．这里距离均方差dRMS 的定义为

(3) 粗略匹配对应点．同理可以对E4进行组合，得到8 点对集E8，乃至16 点对集E16等．在对应点对不是太多的情况下一般得到E4、E8即可．选择E4或E8中距离均方差最小的4 点对或8 点对作为粗略的对应点．

(4) 精确匹配对应点．在目标点集中以粗略对应点为球心，半径为 CR 做球，处于球内的点作为潜在对应点，遍历所有的对应点组合，选择使dRMS 最小的点对组合作为最终的对应点．CR 的选取值越大得到的结果更精确，但耗时也越大．

对Stanford bunny00 和Stanford bunny45 进行上述匹配算法，点对组合至E4，CR 取0.005,mm，得到4对对应点，如图3 所示．从图中可以看到，两视图间的对应点对基本上处于兔子的同一个位置，证实了该匹配算法的有效性．

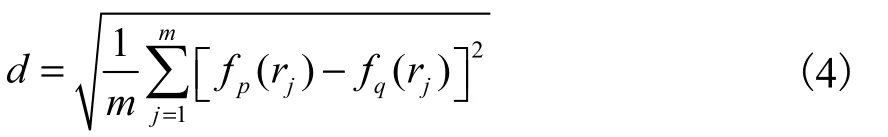
式中：m 为高维曲率图的维数；fp(rj)、fq(ri)分别为点 pi、qi的高维曲率图分量．对 pi的所有潜在对应点按d 的大小进行升序排列，选取靠前的M 个对应的 qi作为 pi最终的潜在对应点．M 的选取原则是尽量保证正确的对应点包括在其中，而且值还不能过大，不然会给后面的匹配算法带来困难．经过实验验证M 值选取为10，即一个点具有10 个对应点时，点云重叠部分的特征点基本都能找到正确的对应点，而且对后续的匹配算法不会增加太多负担．

4 精确匹配对应点

目前主要匹配算法思想是利用形状的空间变换不变性来有效匹配对应点．在众多的算法中，Mitra的贪婪算法虽然不能保证找到最佳的对应点，但它能高效快速地找到接近最佳匹配的对应点对．为了较为精确地匹配对应点，笔者提出下面的两步匹配算法：首先，通过贪婪算法粗略匹配对应点，然后同样利用形状空间变换不变性，遍历这些点某个邻域范围内的所有点对组合，找出最佳对应点．具体算法有如下4 个步骤．

(1) 构造点对．对于源特征点集中的每个点对组合 pi和 pj，从其潜在对应点中选择 qik和 qjl，使得

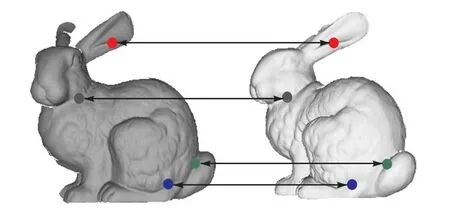
图3 精确匹配对应点Fig.3 Accurately matching of corresponding points

5 结果与讨论

(2) 组合点对．顺序从E2中取出2 点对 ei，再从

针对Stanford bunny00 和Stanford bunny45，配准前如图4(a)所示，利用匹配算法得到对应点以后，运用奇异值分解(SVD)法[19]直接求取刚性变换，将Stanford bunny45 粗略配准到Stanford bunny00 上，得到图4(b)所示结果，可以看到两片点云数据基本上被配准在一起，但仍出现大片单一视图的点云数据，需要进一步的精确配准．

为此，将粗配准后的两片点云数据作为输入，利用经典ICP 算法进一步精配准，ICP 算法的具体算法流程为：

(1) 通过随机采样的方式从源点集中选择一部分点集P；

中日医院呼吸中心烟草病学与戒烟中心主任肖丹教授指出，无论吸什么样的烟，只要吸烟就是有害健康的。大量研究表明，烟草烟雾中有超过7000种化学物质，包括69种致癌物，依然含有尼古丁、丙二醇、丙三醇、重金属等有害物质，会增加患慢性阻塞性肺疾病、肺癌、心血管疾病的风险，可以引起人体中多个器官的损害。

(2) 对点集P 中的任何一点，在目标点集中找寻与之欧式距离最近的点作为对应点，得到点集P的对应点集Q；

(3) 从对应点集P 和Q 中删除距离值大于平均距离的点，剩下的点作为最后的对应点；

(4) 通过对应点求取坐标变换矩阵(四元素法或SVD)；

(5) 构造并计算误差评价函数，其实就是第4 节提到的距离均方差；

(6) 判断误差评价函数的大小是否满足精度要求，如果满足则算法终止，返回结果；如不满足，迭代进入步骤(1)，此时的目标点集为原始目标点集经过步骤(4)获得的变换后的结果．

通过ICP 算法的精配准得到最终的配准结果如图4(c)所示，可以看到两片点云数据交错有致，达到了较好的配准效果．

图4 兔子点云的配准过程Fig.4 Process of registration for Stanford bunny

为了验证本文配准算法的通用性和适应性，利用本实验室的扫描系统，对图5 所示的人头模型进行扫描实验．但这次扫描条件比较特殊，只利用其中的一个摄像机，分别从不同角度进行扫描，得到一系列具有重叠部分的三维点云视图．

图5 人头模型Fig.5 Model of head

图 6 所示为以任意两角度拍摄的两点云视图．运用本文的配准算法模块，对这两点云视图进行配准，得到如图7 所示的结果．图7(a)为配准前的两点云视图在同一坐标系中的表示，可以看出两点云的视图旋转了一定的角度，且存在少量的平移；图7(b)所示为本文算法粗配准后的点云视图，这时两点云数据已经相当接近配准状态；图7(c)为经过ICP 精配准的结果，可以看到视图间的点云交错有致，达到了良好的配准效果，验证了本文算法的有效性．

为说明该算法的抗噪性能，对Stanford bunny00和Stanford bunny45 加入不同程度的白高斯噪声．噪声方差δ分别设为原始点云相邻顶点间平均距离的0.1、0.3 和1.0 倍．为了和同类算法进行比较，在1.0倍噪声时，分别利用旋转图像算法[6]和本文的算法进行粗配准．图8(a)、8(b)分别表示在0.1 倍和0.3 倍噪声下本文算法的配准结果，图8(c)、8(d)分别表示在1.0 倍噪声下利用本文算法和旋转图像算法的粗配准结果．从图中可以看到，本文的配准算法具有很好的抗噪性，即使在1.0 倍噪声下也能达到不错的配准效果，远远优越于旋转图像算法．

图6 不同角度的两点云视图Fig.6 Two views of head with different angles

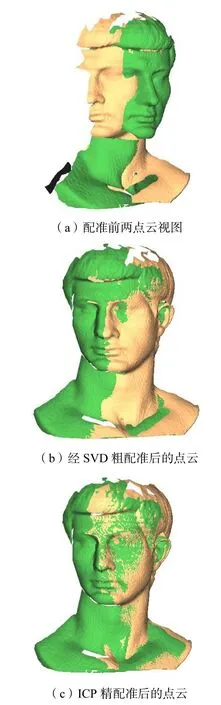
图7 人头点云的配准过程Fig.7 Process of registration for the head

图8 不同高斯噪声下的点云配准结果Fig.8 Results of registration for Stanford bunny with different noise levels

为了进一步说明该算法在寻找对应点上的时间复杂度，以体积分(integral volume descriptors)算法[4]作对比．针对点云数据Bunny、Chicken、Dragon[15]，以Bunny000、Chicken_view1 和Dragonstandright_0作为源点集，Bunny045、Chicken_view2 和Dragonstandright_24 作为目标点集．在相同硬件条件下，在源点集中选取相同的100 个特征点，然后分别利用曲率图和体积分算子在对应的目标点集中寻找对应点，每个特征点的对应点数量设定为20，实验结果如表1所示．由于本文的匹配算法是通过两步法的思想寻找对应点，只对很少的部分点集进行了高维曲率图计算，所以耗费的时间也大大少于体积分算子．

表1 曲率图和体积分算子找到对应点的耗时对比Tab.1 Comparison of the point matching time for some models

6 结 语

本文在点几何表示的三维点云数据中，构造了一维、高维曲率图．并利用曲率图分两步确立了具有重叠部分的三维点云数据间的对应点．先利用一维曲率图粗略找对应点，然后对找出的点进行高维曲率图运算，剔除大量错误对应点．在此基础上，通过改进的贪婪算法实现了对应点之间的精确匹配．找到匹配点对后，通过SVD 求解刚性变换，将两片点云数据粗略配准到ICP 算法的收敛域，最后借助经典ICP算法实现了点云数据的精确配准．通过各种配准实验，体现了该算法不但具有很强的抗噪性，在计算时间上也大大优于其他基于特征点的配准算法．

致 谢：

特别感谢卡内基美隆大学机器人研究所的Daniel Huber 教授提供了利用旋转图像进行三维点云数据配准的可执行代码．同时感谢斯坦福大学的计算机图形学实验室提供的三维点云数据．

2006.

［9］Johnson A，Hebert M. Using spin images for efficient object recognition in cluttered 3D scenes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，1999，21(5)：674-686.

［10］Frome A，Huber D，Kolluri R，et al. Recognizing objects in range data using regional point descriptors[J].Computer Vision-ECCV，2004，3023：224-237.

［11］Gatzke T，Grimm C，Garland M，et al. Curvature maps for local shape comparison[C]//IEEE International Conference on Shape Modeling and Applications. 2005：244-253.

［12］Mitra N J，Gelfand N，Pottmann H，et al. Guibas registration of point cloud data from a geometric optimization perspective [C]//Proc Symposium on Geometry Processing. 2004：23-32.

［13］Gray A. Modern Differential Geometry of Curves and Surfaces[M]. Boca Raton，FL，USA：CRC Press，1993.

［14］Huy Tho Ho，Gibbins Danny. Multi-scale feature extraction for 3D models using local surface curvature [C]//Digital Image Computing：Techniques and Applications.2008：16-23.

［15］Cazals F，Pouget M. Estimating differential quantities using polynomial fitting of osculating jets[J]. Computer Aided Geometric Design，2005，22(2)：121-146.

［16］Lange C，Polthier K. Anisotropic smoothing of point sets[J]. Compute Aided Geometric Design ， 2005 ，22(7)：680-692.

［17］Alexa M，Behr J，Cohen-Or D，et al. Point set surfaces[C]// Proceedings of IEEE Visualization. 2001：21-28.

［18］Stanford University. Stanford 3D Scanning Repository[EB/OL]. http：//www-graphics. stanford. edu/data/3Dscanrep/.

［19］Arun K S，Huang T S，Blostein S D. Least-squares fitting of two 3-D point sets[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence ， 1987 ，9(5)：698-700.