一种滚珠丝杠扭转振动模态的测量与分析方法

周 勇 王国贤 曹小华

武汉理工大学，武汉，430063

0 引言

滚珠丝杠副进给驱动是目前数控机床上应用最广泛的进给驱动设备，相对直线电机驱动，它具有成本低、易于控制、维护简单等优点。高速加工技术要求机床的进给驱动机构具有高速度和高加速度，然而，细长的丝杠在高速、高加速度运行过程中会引起扭转、轴向和弯曲变形及振动，这种变形和振动会影响零件的加工质量、加剧刀具磨损甚至导致控制系统的不稳定，也限制了机床进给速度和加速度的进一步提高。

在滚珠丝杠副驱动中，滚珠丝杠的扭转振动是实现高带宽和高定位精度的决定性影响因素之一［1-3］。由于滚珠丝杠副进给驱动系统一般采用半闭环控制，其位置和速度反馈是从电机码盘或丝杠上安装的角度编码器获取的，因此，转子－丝杠系统的扭转振动被包含在控制系统的位置、速度控制环中。此外，在实际机床的加工过程中，工作台的位置是不断变化的，而且被加工件往往有很高的金属切除量，从而不可避免地会导致控制性能上的偏差，进而影响到机床的加工精度。因此，有必要对滚珠丝杠副进给驱动机构的扭转振动模态进行精确分析，充分考虑其动力学行为对控制的影响，进而对控制系统进行有效的补偿。目前，对于滚珠丝杠扭转振动模态的研究通常采用有限元或集中参数等方法建立其动力学模型［4-10］，但是由于滚珠丝杠副进给驱动机构的结构复杂性，仅仅依靠理论分析很难得到精确结果，还必须结合必要的实验研究。

在滚珠丝杠副进给驱动系统中，电机驱动力矩难以精确测量，而且丝杠上也难以布置多个测点，因此，对其扭转振动模态的测量很难采用常规的通过测量多点激励－响应的方式进行。本文提出一种滚珠丝杠扭转振动模态测量与分析方法:在丝杠尾端安装一个旋转编码器，测量电机码盘和尾端旋转编码器的角加速度信号，对测量信号进行频域分析，并结合滚珠丝杠副进给驱动机构扭转动力学理论计算模型，获得其扭转振动模态。研究结果可为滚珠丝杠副进给驱动扭转动力学分析及其高带宽控制提供科学依据。

1 滚珠丝杠副进给驱动机构扭转动力学模型

图1为本文所研究的滚珠丝杠副进给驱动机构转子－丝杠系统的示意图。采用有限元方法，将转子－丝杠系统划分为若干个扭转单元。由于联轴器的刚度是非均匀分布的，故将联轴器按输入端和输出端分开，分别建立有限元单元，输入端和输出端之间的扭转刚度采用联轴器的标称刚度。对于工作台和螺母等移动部件，忽略工作台与滑轨之间的接触刚度的影响，将其作为集中质量来考虑，并按照动能相等的原则，折算到丝杠轴上作为等效惯量。

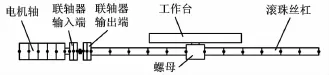
图1 转子-丝杠扭转系统有限元-集中参数模型

对于均质杆单元，利用形函数方法，可得到其单元惯量矩阵［7］:

式中，l为单元的长度;jl为杆单元的单位长度转动惯量;下标i表示节点编号。

杆单元的单元刚度矩阵为

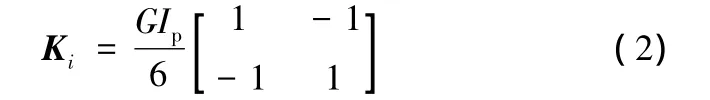
式中，G为杆单元的剪切弹性模量;Ip为杆单元的截面极惯性矩。

对于工作台等直线运动部件，建立扭振动力学模型时，应将它们的质量换算成等效转动惯量，然后把它们看作惯量元件。换算的原则是保持转换前后动能相等［11］，即

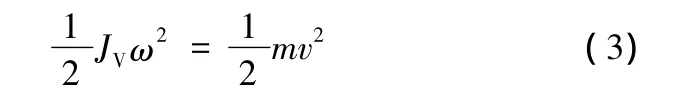
式中，ω为丝杠角速度;v为移动部件速度;m为移动部件质量;JV为等效转动惯量。

在将等效惯量转换到滚珠丝杠对应单元上时，就将其视为丝杠上的一附加惯量元件。取丝杠导程为ξ，于是由几何关系可得

将式(4)代入到式(3)后得移动部件的等效惯量:

将各单元所作的分析结果进行综合，分别对单元惯量矩阵和单元刚度矩阵进行组集，可得到全系统整体惯量矩阵M和整体刚度矩阵K。

联轴器扭转刚度采用集中刚度kct，对其组集的方法如下:取kct相邻的两个单元组成的子系统，如图2所示，则子系统在t时刻的变形势能为

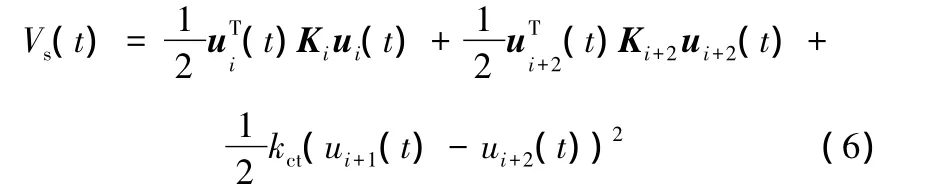
式中，ui(t)=［ui(t)ui+1(t)］T，ui+j(t)(j=0，1，2，3)为单元节点的角位移。

图2 考虑联轴器集中刚度的单元子系统

取角位移列矢量u'i(t)=［ui(t)ui+1(t)ui+2(t)ui+3(t)］T，则式(6)可变为

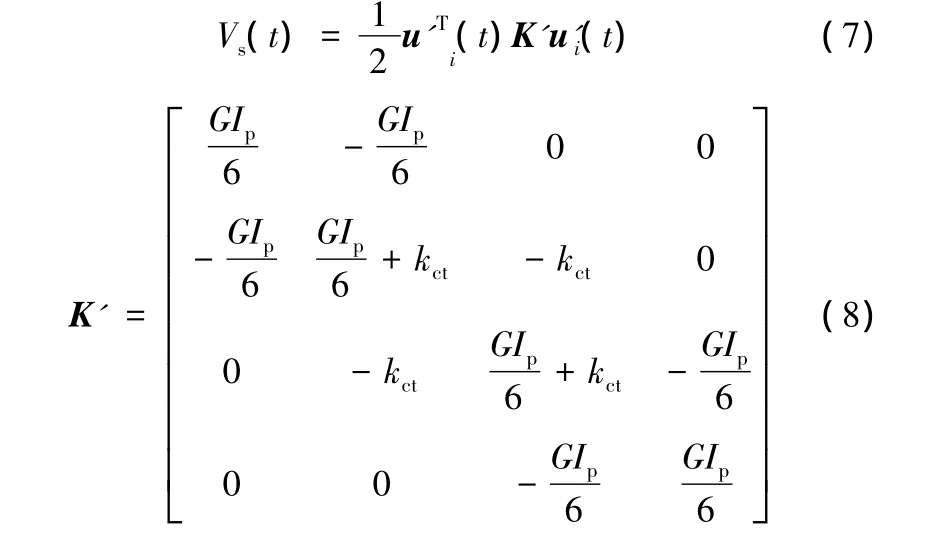
以各独立节点的角位移作为其动力系统的广义坐标，记作qi，相应广义坐标的广义力记为Qi，i=1，2，…，n(n为考虑系统边界条件后的独立变形节点个数)。则由拉格朗日动力学方程可得到全系统的动力学方程:

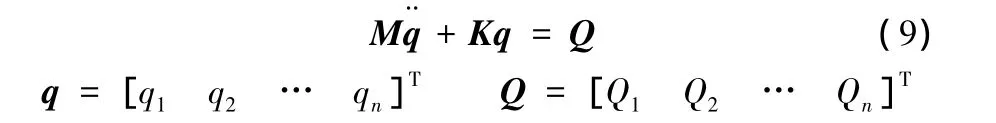
对该动力学方程进行求解，即可得到滚珠丝杠副驱动机构扭转振动的各阶模态固有频率和振型。但是，由于滚珠丝杠上开有螺旋槽，其转动惯量和刚度的计算不能简单按照直圆轴处理，只能确定它们的取值在一定的范围之内，因而根据该方程通过仿真进行求解，需要结合实验对其参数进行适当调整。当采用一组取值合理的参数组合，经过模拟试算的结果与实验结果相吻合时，模拟计算结果和试验结果皆有效。

2 扭转振动测量装置及方法

本文测量装置如图3所示，主要包括滚珠丝杠副进给驱动系统(含数控装置、伺服驱动器、伺服电机、联轴器、滚珠丝杠、螺母、工作台等)、旋转编码器、计数卡以及计算机等。通过计数卡可实时测量安装在丝杠尾端的旋转编码器信号和伺服电机码盘信号。旋转编码器为德国Heidenhain公司制造的ERN120系列，其物理分辨率为5000脉冲每转，经4倍频后可达到20 000脉冲每转。伺服电机码盘的分辨率为6000脉冲每转，经4倍频后可达到24 000脉冲每转。计数卡为阿尔泰科技制造的PCI2394型4轴正交编码器和计数器卡，通过PCI接口安装在计算机内，可同时测量4个通道的脉冲/方向信号。测量软件基于实时Linux系统开发，计数采样频率可达到10kHz。

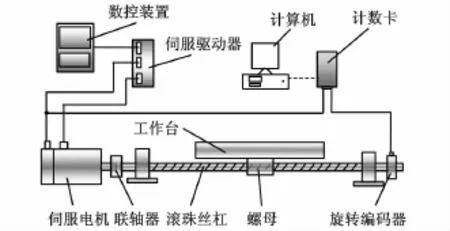
图3 测量装置示意图

测量时，首先打开测量软件，设置采样周期、锁存数据频率、计数通道的个数等;然后进入测量等待状态，数控系统指令工作台按照一定的位置、速度运动，当运动开始时，电机码盘和旋转编码器随电机转子－丝杠系统一起旋转，计数卡的计数器模块被触发并开始按照设定的采样周期对码盘和旋转编码器脉冲信号进行计数，当程序计数完成后将自动停止计数(在采样周期低的时候可以通过键盘输入中止程序);最后执行保存数据操作，即将测量数据保存至计算机，所测得的数据为一定时间间隔的脉冲个数，根据码盘或旋转编码器的分辨率可得到实际的转角值，由于是按照一定的采样周期计数，故角速度和角加速度可通过差分运算得到。

丝杠的扭转振动是在丝杠大位移旋转运动过程中同时发生的运动现象，对于测量信号，需要消除丝杠大位移运动的影响。可截取工作台匀速运动段的角位移数据，并经两次差分运算后得到角加速度信号，则该加速度信号包含扭转振动信号且理论上平均加速度为零。对不同测点信号作互功率谱分析，可反映两个信号在频域中所得两种谱的共同成分及其相位差关系等。为抑制噪声和测量误差影响，可对同一测点取两次测量信号作互功率谱分析，得到该测点振动信号的频域特征。

由于滚珠丝杠上难以布置多个测点，通过两个测点仅能得到扭转振动的频率信息，而无法得到其振动阶次和振型，又考虑到扭转振动模态一般不是密集模态，其各阶频率值相差较大，故可通过建立的滚珠丝杠副进给驱动机构扭转动力学模型获得其理论扭转振动模态固有频率和振型，并根据测量结果对模型参数进行适当调整，当前几阶扭转振动固有频率与实验结果一致时，即可认为所得到的理论模态与实际相符。

3 实例研究

本文所建立的实验平台见图4，对其X轴扭转振动模态进行了测量与分析。该实验平台X轴主要计算参数如表1所示。

图4 实验平台照片

表1 X轴主要计算参数

让X轴拖板处于丝杠中间位置，指令其作直线进给运动，取进给位移为25mm，进给速度为6000mm/min(100mm/s)，加 速 度 为 0.5g(5m/s2)。截取X轴作匀速运动时的加速度信号作频域分析，图5所示为电机码盘信号与旋转编码器信号的互功率谱幅频曲线，图6所示为旋转编码器两次测量信号的互功率谱幅频曲线。从图5和图6可以看出，主要的振动频率为19Hz、54Hz、90Hz、352Hz和 700Hz。

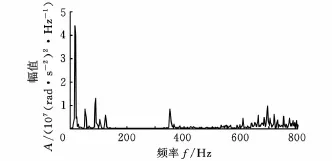
图5 电机码盘信号与旋转编码器信号的互功率谱幅频曲线

图6 旋转编码器两次测量信号的互功率谱幅频曲线

利用MATLAB编制滚珠丝杠副进给驱动机构扭转振动模态数值计算程序，图7和图8分别为第1阶和第2阶扭转振动模态固有频率和振型图(取电机自由端振幅为1)。结合实验测量结果与数值计算结果，可以判断，352Hz为第1阶扭转振动固有频率，700Hz为第2阶扭转振动固有频率。实验结果与数值计算结果误差不超过1%，可以认为理论计算模态振型符合实际。需要说明的是，频率19Hz、54Hz和90Hz可能与移动部件的轴向振动及工频信号干扰相关，有待进一步研究。

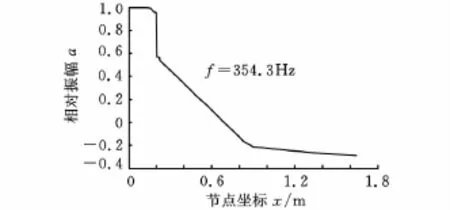
图7 第1阶扭转振动模态振型图

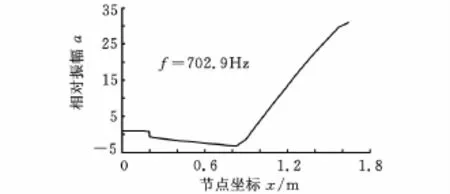
图8 第2阶扭转振动模态振型图

4 应用前景

本文提出的测量和分析方法可用于新产品试制过程中的滚珠丝杠副进给驱动系统的扭转动力学分析，实现滚珠丝杠副驱动机构的结构优化，还可以直接用在进给驱动系统的控制系统之中，构建性能更优的控制方式。如滚珠丝杠副进给驱动机构的扭转振动会限制系统的控制带宽并劣化机床的加工质量，通常在伺服驱动器速度环中利用陷波滤波器进行补偿(图9)。利用本文提出的测量和分析方法，可准确得到系统的扭转振动频率及振型，为陷波滤波器的参数自适应调整及补偿效果的验证提供科学依据。

图9 扭转振动的陷波滤波补偿

5 结语

本文提出了滚珠丝杠副驱动机构的扭转振动模态的测量和分析方法，对安装在滚珠丝杠尾端的高分辨率旋转编码器信号和伺服电机码盘信号进行了测量和分析，并对所建立的驱动机构转子－丝杠系统有限元－集中参数模型进行了数值计算，可精确得到系统扭转振动模态前两阶固有频率和振型，克服了滚珠丝杠副驱动机构的扭转振动模态难以精确测量和分析的困难。该方法可用于滚珠丝杠副驱动机构的结构优化、控制系统陷波滤波器的参数自适应调整及补偿效果的验证等。

［1］Smith D A.Wide Bandwidth Control of High－speed Milling Machine Feed Drives［D］.Gainesville:Univ.of Florida，1999.

［2］Erkorkmaz K，Kamalzadeh A.High Bandwidth Control of Ball Screw Drives［J］.Annals of CIRP，2006，55(1):393-398.

［3］Kamalzadeh A，Erkorkmaz K.Accurate Tracking Controller Design for High－speed Drives［J］.International Journal of Machine Tools and Manufacture，2007，47(9):1393-1400.

［4］Poignet P，Gautier M，Khalil W.Modeling，Control and Simulation of High Speed Machine Tool Axes［C］//Proceedings of IEEE International Conference on Advanced Intelligent Mechatronics.Atlanta，1999:617-622.

［5］Zaeh M F，Oertli T.Finite Element Modeling of Ball Screw Feed Drive System［J］.Annals of CIRP，2004，53(1):289-292.

［6］Whalley R，Ebrahimi M，Jamil Z.The Torsional Response of Rotor Systems［J］.Proceedings of the Institution of Mechanical Engineers，Part C:Journal of Mechanical Engineering Science，2005，219(4):357-380.

［7］Zhou Y，Peng F Y，Chen J H.Torsion Vibration Analysis of Lead－screw Feed Drives with Changeable Table Position and Work－piece Mass［C］//Proceedings of IEEE International Conference on Mechatronics and Automation.Harbin，2007:2194-2199.

［8］左健民，王保升，汪木兰.数控机床进给系统刚度分析及前馈补偿控制研究［J］.机械科学与技术，2008，27(3):386-389.Zuo Jianmin，Wang Baosheng，Wang Mulan.Analysis and Feedforward Compensation Control of Stiffness in a CNC Machine Tool Feed System［J］.Mechanical Science and Technology，2008，27(3):386-389.

［9］Okwudire C E，Altintas Y.Hybrid Modeling of Ball Screw Drives with Coupled Axial，Torsional，and Lateral Dynamics［J］.ASME Journal of Mechanical Design，2009，131(7):071002.1-071002.9.

［10］范大鹏，范世珣，鲁亚飞，等.数控机床高性能传动部件控制技术的研究进展［J］.中国机械工程，2011，22(11):1378-1385.Fan Dapeng，Fan Shixun，Lu Yafei，et al.Current Status of Control Research on NC Machine Transmission Component［J］.ChinaMechanicalEngineering，2011，22(11):1378-1385.

［11］王祺.内燃机轴系扭转振动［M］.大连:大连理工大学出版社，1991.