基于耐撞性拓扑优化的汽车关键安全件设计

聂 昕 黄鹏冲 陈 涛 成艾国

湖南大学汽车车身先进制造国家重点实验室，长沙，410082

0 引言

随着我国居民汽车保有量的不断提高，国内车辆C－NCAP星级评价体系的完善，人们对于汽车碰撞安全性能的认知也日益提高，汽车的安全性能也如同舒适性和动力经济性，成为了人们购买汽车时考虑的重要性能之一。

在车辆传统的设计开发阶段，对于车身关键安全件的设计都是依靠设计师的经验或类比设计进行初始设计，然后通过大量的零部件及整车试验，并对试验结果进行分析和优化，才得出最终的设计方案。这不仅需要大量的人力、物力，而且只是在原有的设计基础上进行优化，很难对原始的结构进行较大的改进。结构拓扑优化可以在给定的设计区域获得最佳的材料分布形式，同时满足给定的约束条件。在碰撞关键区域的初始设计阶段采用拓扑优化方法，不失为一种很好的选择。国外学者对于碰撞的拓扑优化做了大量的研究:Park［1］运用等效静态载荷(equivalent static loads，ESL)方法，求解线性动态响应、非线性静态响应和非线性动态响应等结构优化问题;Ortmann［2］通过数学模型来描述拓扑模型结构的横截面，运用Graph－Heuristic方法通过数学优化算法求解动态加载的结构拓扑优化问题;Inou等［3］将自动网格模型(cellular automaton，CA)模型引入到拓扑优化方法中，其后，Patel等［4］在此基础上整合非线性带罚函数的实体变密度法(solid isotropic microstructures with penalization，SIMP)插值模型，提出以LS－DYNA为求解基础的非线性拓扑优化方法。国内学者对于耐撞性拓扑优化研究也已逐渐展开［5-6］，但研究的广度和深度相对滞后，主要还停留在以模型刚度、强度为拓扑优化目标，进而研究车辆的碰撞性能这一阶段。

本文以某设计开发阶段的国产车辆为基础，针对其在分析过程中存在的侧面碰撞侵入量较大及偏置碰门槛梁折弯等现象，运用耐撞性拓扑优化方法，建立门槛梁的等效拓扑优化模型，对门槛梁及其内部结构的材料分布进行重新定义。

1 耐撞性拓扑优化基本原理

1.1 HCA方法简介

自动混合元网格模型［7］(hybrid cellular automaton，HCA)方法是一种自动的CA网格处理方法。CA是由规则网格组成的离散计算模型，其中每个单元都有自己独立的有限维向量的特点，同时每个单元的计算信息都是由其相邻单元的节点和两者之间的相对半径来确定的。这种相邻单元的信息构成贯穿于整个计算求解迭代过程。这种单元的离散特性可以免除拓扑优化过程中对于梯度信息的处理，能够很好地应用于动态加载方式的拓扑优化问题。在拓扑优化过程中，CA模型与有限元模型中的网格之间存在一一对应的关系。图1所示为CA网格模型的3种典型相邻位置信息。

1.2 材料参数化

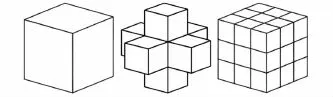
图1 典型的CA模型相邻位置信息

根据HCA方法的网格特性，材料参数化结合变密度法［8］以及 SIMP［9-10］插值模型进行设定。基于SIMP插值模型，Patel等［4］提出一种非线性插值方法，将材料属性映射到相对密度单元中，在能量与材料相对密度之间获得两者的相互关系。同时引入模型发生塑性变形时，材料屈服极限和应变硬化模量的插值模型，以保证材料参数在碰撞过程中的正常应用。该数学模型可表示为

式中，ρ为材料密度;E为弹性模量;σY为屈服极限;Eh为应变硬化模量;p、q为惩罚因子。

1.3 设计目标

对于类似碰撞类型的动态拓扑优化问题，往往是要求在其结构能够吸收更多能量的同时，保证碰撞过程中的结构完整性。该数学模型为

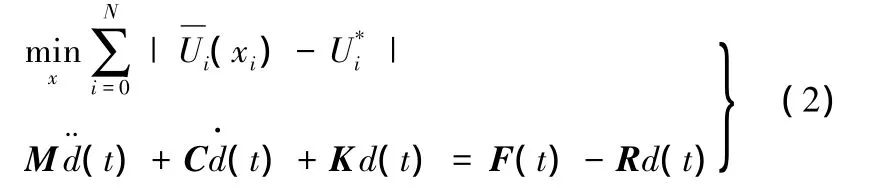
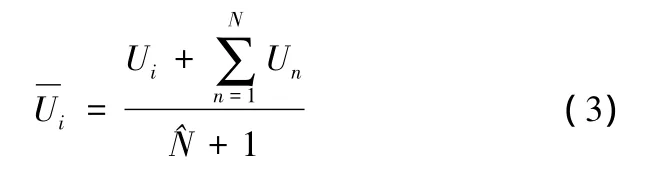
式中，Ui为第i个单元的内部能量密度;Un为第i个单元的第n个相邻单元的内部能量密度;^N为第i个单元相邻单元的总数。

该数学模型还需满足以下条件:

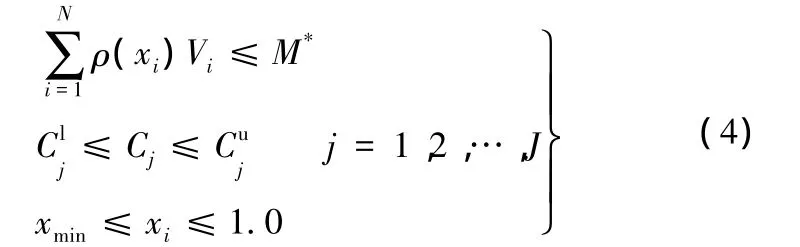
式中，Vi为第i个单元的体积;M*为设计目标质量;Cj为模型中第j个约束;上标l和u表示相关约束的上下边界。

1.4 仿真求解及优化过程

采用LS－DYNA求解器为计算基础，在每次迭代过程中，材料的重新分布都会伴随着单元的增加或删除。为保证材料在重新分布过程中计算求解的稳定性，对材料相对密度做以下约束:

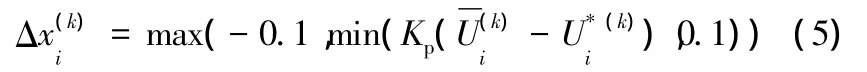
其中，Kp为比例因子，最大相对密度的改变量为±1，这是为了保证在迭代过程中的稳定性，k为迭代次数。在某次迭代过程中，材料的相对密度等设计变量会发生改变，这会成为下一次迭代的初始变量，直到满足整体约束的收敛条件。图2所示为耐撞性拓扑优化基本过程。

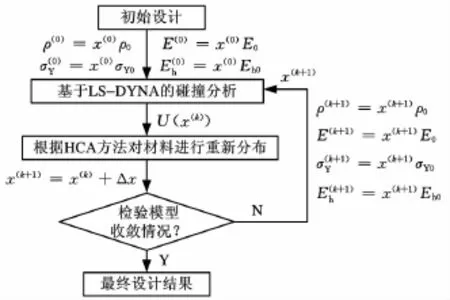
图2 耐撞性拓扑优化基本过程

1.5 收敛准则

对于质量控制的拓扑优化过程，以质量为约束条件，在每次迭代过程中的质量变化可表示为

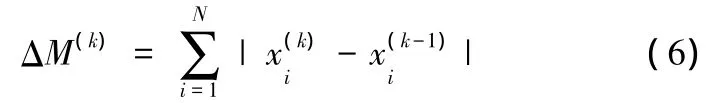
当质量变化满足以下条件时，模型满足收敛条件:

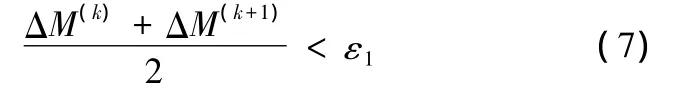
式中，ε1为质量收敛误差因子。

2 门槛梁拓扑优化模型

2.1 门槛梁有限元模型

图3所示为正面碰撞和侧面碰撞过程中碰撞作用力的传递情况。门槛梁作为主要传递路径，在传递碰撞作用力的同时还要保证乘员舱的结构完整性，避免产生较大的侵入。在侧面碰撞过程中，门槛梁的Y向变形情况直接影响了B柱、内饰等部件对于人体的损伤情况。针对门槛梁对于车辆安全性能的重要性，本文以某设计开发阶段的国产车辆为基础，依据总布置的设计需求和门槛梁初始设计的基本尺寸，将门槛梁本体作为设计区域，建立由22 100个3D实体单元组成的门槛梁有限元模型，通过等效圆柱体来分别模拟偏置碰撞过程中轮胎对门槛梁的冲击作用和侧面碰撞过程中B柱变形对门槛梁产生的冲击作用。图4所示为门槛梁正面40%偏置碰撞和侧面碰撞的等效有限元模型。

图3 正面碰撞和侧面碰撞作用力传递情况

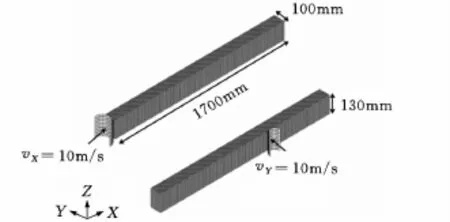
图4 门槛梁等效有限元模型

2.2 初始变量

作为车辆碰撞过程中的主要传递路径，门槛梁及其内部的加强板结构的材料一般都选用高强度钢，以确保门槛梁有足够的抗弯强度，以满足车辆碰撞过程中对于乘员舱的保护作用。在门槛梁模型的建立过程中，以普通钢材的材料参数对模型的密度、弹性模量、屈服应力等初始变量进行设定，如表1所示。

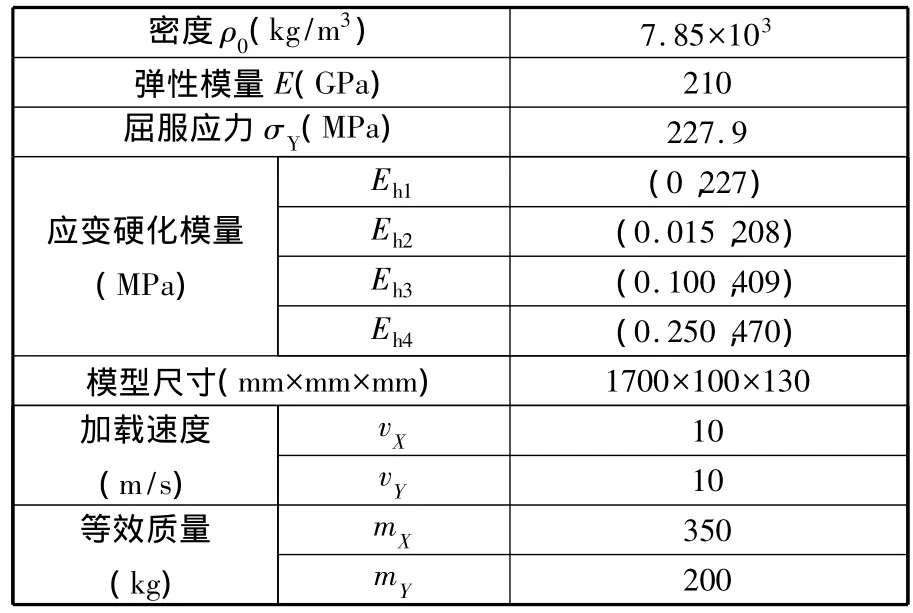
表1 拓扑优化初始变量

在模拟过程中，等效刚性圆柱体加载情况对于拓扑优化结果的正确与否起着关键作用。以正面40%偏置碰撞为例，碰撞过程中，轮胎会对门槛梁产生一定的冲击作用，截取门槛梁前端在碰撞过程中的截面力－时间曲线，根据动量守恒定律:

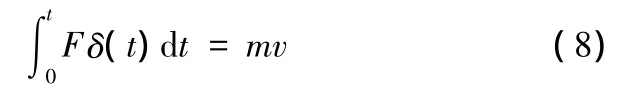
式中，F为碰撞力;δ(t)为微位移;m为碰撞质量;v为碰撞速度。

可求解出轮胎在碰撞瞬间的冲击动量。在正面40%偏置碰撞过程中车辆的加载速度为17.8m/s，经过前舱吸能盒、大梁等主要吸能部件对碰撞能量的吸收，轮胎对于门槛梁的冲击速度会有一定程度的减小，人为选取vX=10m/s，即可获得刚性圆柱体的等效质量。对于侧面碰撞而言，侧碰小车的初始加载速度为13.8m/s，碰撞过程中，侧碰小车前方蜂窝铝的压溃变形以及B柱的弯曲都会使侵入速度减小，故取vY=10m/s，通过截取B柱下方Y向的截面力－时间曲线，即可获得侧面碰撞刚性圆柱体等效质量。

2.3 边界条件

为保证门槛梁有足够的强度来抵抗碰撞的冲击载荷，同时降低生产制造过程中的材料消耗，选取拓扑优化的最终质量参数为0.3。

在正面40%偏置碰撞过程中，为避免门槛梁在轮胎的冲击作用下产生较大的折弯变形，在门槛梁前端施加最大X向位移为20mm的约束条件。对于侧面碰撞而言，为降低碰撞过程中的侵入量，在B柱下方门槛梁对应位置加载Y向最大位移为30mm的约束条件。

结合式(2)和式(3)，门槛梁的偏置碰撞和侧面碰撞并行运算的数学模型可表示为

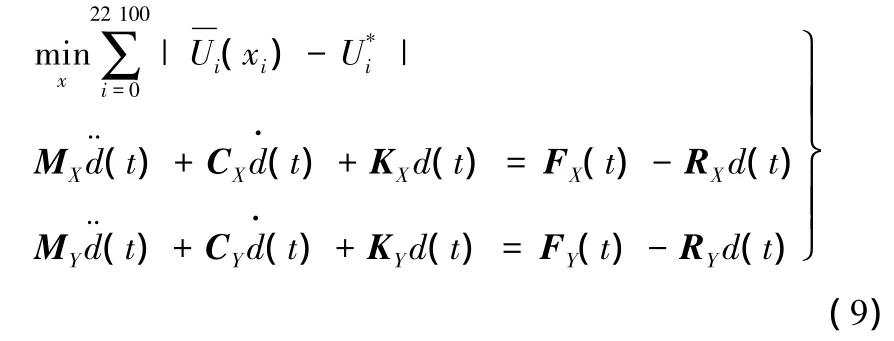
并满足以下条件:

2.4 拓扑优化结果及收敛情况

拓扑优化模型以4核、内存为4G的HP Z600台式工作站为运算载体，平均每次迭代所需要的时间约为5min。经过47次的迭代，模型趋于收敛，并得到最终的拓扑优化模型。图5所示为拓扑优化结果;图6所示为门槛梁Y向结构拓扑优化迭代过程;图7所示为拓扑优化基于模型质量的收敛情况。图8所示为拓扑优化过程中X向和Y向的位移情况，其中X向最大位移为12.5mm，Y向最大位移为26.8mm，均满足拓扑优化的初始边界条件。

图5 拓扑优化最终结果

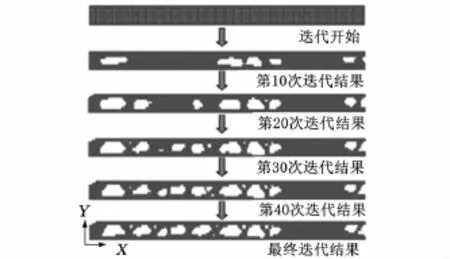
图6 门槛梁Y向结构拓扑优化迭代过程

图7 拓扑优化收敛情况

图8 门槛梁X向与Y向位移情况

3 工程诠释及耐撞性验证

3.1 工程诠释及工艺修正

分析拓扑优化结果，整体的材料分布情况为腔体结构，与实际车辆门槛梁结构基本一致。对于门槛梁而言，更改其钣金结构会对车辆整体造型造成一定的影响。门槛梁在实际工程装配过程中，不仅要考虑B柱、侧围等车身部件的搭接情况，同时还必须在门槛梁内部预留出空调管路和车内电子系统线路布置的必要空间。本文沿用原始设计的门槛梁内外钣金件结构，在保留总布置以及装配所需要的各种定位孔、过线孔的基础上，根据拓扑优化后的材料分布，在门槛梁外板的相对位置作冲孔处理，同时更改内外钣金厚度和材料属性使其与拓扑优化结果的材料分布情况趋于一致。图9为门槛梁外板结构示意图。

图9 门槛梁内外钣金件结构示意图

对于门槛梁内部结构而言，将门槛梁的材料分布结果沿X轴方向分成4个部分，如图10所示。对比门槛梁的内部加强板结构，第①部分和第③部分的Y向加强结构与拓扑优化结果的材料分布情况在位置上有一定的差异，但整体的结构基本一致。在优化结果中沿用初始设计的第①部分和第③部分的Y向加强板结构，适当修改该区域内部钣金的材料属性，以弥补其在相对位置上的差异。就第②部分而言，由于总布置的设计需求，在该区域内存在必要的安装定位孔，故建立图10所示的优化后带有筋条结构的内部加强板，并对其加载适当的材料属性，使其在整体结构上与材料分布结果趋于一致，同时满足该区域的耐撞性的需求。对于第④部分，从材料的分布情况可以看出，该区域内材料分布较为密集，故在此区域内增加内部加强板，并使用高强度钢，保证该区域的耐撞性需求。拓扑优化后，门槛梁总成的质量由原始设计的14.1kg降低到12.4kg，质量降低了12.1%。

图10 拓扑优化结果工程诠释

3.2 耐撞性验证

建立精确的整车碰撞有限元模型，车身由薄壁钣金件连接而成，主要采用2D壳单元进行整车结构建模，模型包括门盖系统、发动机、座椅和假人等，整车单元数为982 844，整备质量为1230kg。将拓扑优化结果的工程诠释模型装配到整车模型中，并分析整车偏置碰撞和侧面碰撞的耐撞性能。图11所示为整车有限元模型，图12所示为整车偏置碰撞结果，图13为侧面碰撞B柱、门槛梁的的变形截面图。

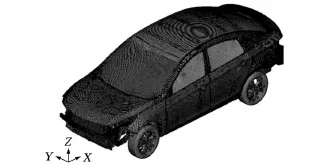
图11 整车有限元模型

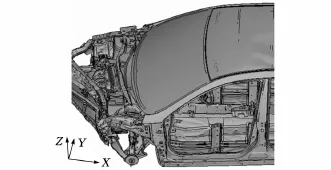
图12 偏置碰撞结果图

图13 侧面碰撞B柱、门槛梁等变形截面

对于正面40%偏置碰撞，优化前后门槛梁变形对比情况如图14所示。优化后，门槛梁的X向压溃量由20.3mm降低到13.8mm。优化后门槛梁上没有明显的折弯变形，能够更好地承受轮胎对于门槛梁的冲击作用，同时保证碰撞后左前门的正常开启、不受门槛梁变形的影响。

图14 拓扑优化前后门槛梁变形对比

表2所示为门槛梁更改前后侧面碰撞过程中乘员舱的侵入情况。车辆在碰撞过程中，车辆B柱相对假人各个部位的侵入量和侵入速度都有一定程度的降低，尤其是骨盆位置的侵入量、侵入速度的变化率都高于胸部和腹部位置的变化率。这对于车辆在侧面碰撞过程中对乘员的保护起着关键性的作用。

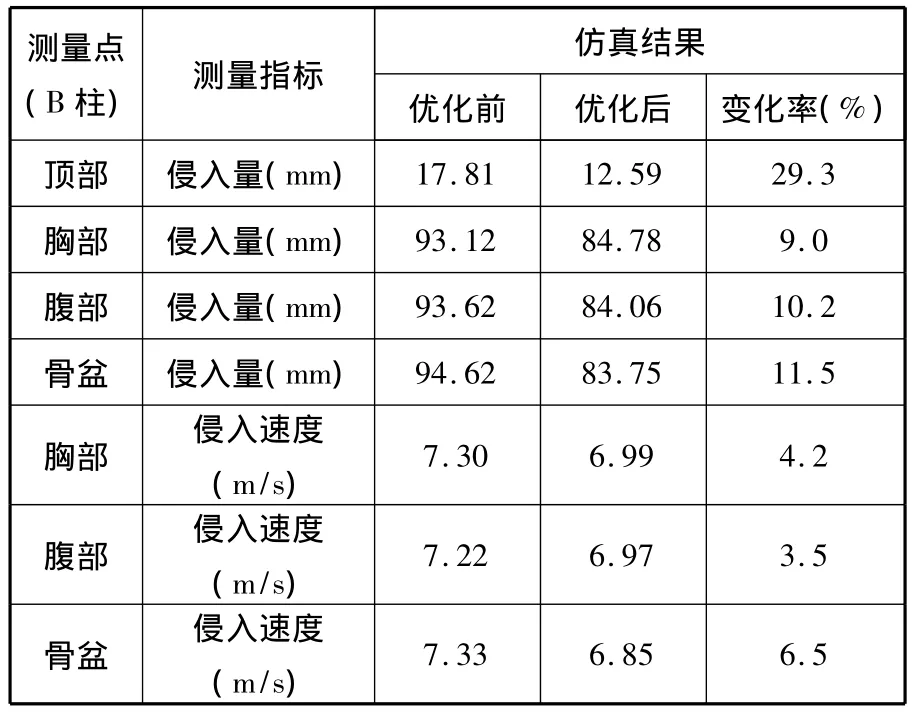
表2 拓扑优化前后乘员舱侵入情况

4 结语

本文运用耐撞性拓扑优化方法，对目标车辆的门槛梁进行拓扑优化，以获得其最优的材料分布情况，并进行必要的工程诠释和工艺修正，最终得到门槛梁的拓扑优化结果。优化后门槛梁总成的质量由原始设计的14.1kg降低到12.4kg，降低了12.1%;整车的偏置碰撞过程中门槛梁的X向压溃量由20.3mm降低到13.8mm;侧面碰撞过程中，B柱相对于假人骨盆位置的侵入量降低了11.5%，侵入速度降低了6.5%，这对于保护车内司乘人员起着至关重要的作用。

运用耐撞性拓扑优化方法对车辆关键安全件进行设计，可以在车身设计的前期得出零件的材料分布情况，避免设计过程中零件的反复修改。有利于缩短设计周期，降低车辆设计开发费用，降低人力、物力成本，同时还能提高车辆的碰撞安全性能，对车辆安全性设计具有很好的指导作用。

［1］Park G J.Technical Overview of the Equivalent Static Loads Method for Non－linear Static Response Structural Optimization［J］.Struct.Multidisc Optim.，2011，43(3):319-337.

［2］Ortmann C.Graph and Heuristic Based Topology Optimization of Crash Loaded Structures［J］.Struct.Multidisc Optim.，2013，47(6):839-854.

［3］Inou N，Shimotai N，Uesugi T.Cellular Automaton Generating Topological Structures［C］//Second European Conference on Smart Structures and Materials.Glasgow，UK，2011:47-50.

［4］Patel N M，Kang B S，Renaud J E.Topology Synthesis of Structures under Impact Loading Using a Hybrid Cellular Automaton Algorithm［C］//Proceedings of the 11th AIAA/ISSMO Symposium on Multidisciplinary A-nalysis and Optimization.Portsmouth，VA，2006:1-19.

［5］舒磊，方宗德.汽车子结构的复合域拓扑优化［J］.汽车工程，2008，30(5):35-37.Shu Lei，Fang Zongde.Design of Composite Domain Topology Optimization for Vehicle Substructure［J］.Chinese Journal of Automotive Engineering，2008，30(5):35-37.

［7］Tovar A.Bone Remodeling as a Hybrid Cellular Automaton Optimization Process ［D］. Notre Dame:University of Notre Dame，2004.

［8］Bendsoe M P，Kikuchi N.Generating Optimal Topologies in Structural Design Using Homogenization Method［J］.Computer Methods in Applied Mechanics and Engineering，1998，2:197-224.

［9］Rozvany G I N，Bendsoe M P，Kirsh U.Optimality Criteria a Basis for Multidisciplinary Optimization［J］.Appl.Mech.Rev.，1994，48:41-119.

［10］Yoon G H，Kim Y Y.Topology Optimization of Material－Nonlinear Continuum Structures by the Element Connectivity Parameterization［J］.Int.J.Numer.Methods Eng.，1997，69:2196-2218.