三层平板导体厚度及电导率的涡流检测

任芳芳，雷银照

（北京航空航天大学自动化科学与电气工程学院，北京 100191）

不导磁的层状平板导体常见于航空、航天设备中，以多层金属复合板、多层平板导电涂层为其典型结构。为确保功用的充分发挥，多层平板导体在诸多参数上均有要求，其厚度及电导率不仅能够指示多层平板导体的磨损、老化、腐蚀程度，亦能反映多层导体内部的物理、化学变化，因而需要有效的检测技术来检测这些参数。

采用涡流检测法对多层不导磁平板导体进行无损检测，具有精度高、速度快、操作简单、成本低廉等优势。其正问题的求解模型可归结为多层平板导体上方线圈阻抗解析表达式的计算。目前已发表的文献中，多层平板导体上方空心圆柱线圈［1－3］、椭圆线圈［4］的阻抗计算方法均已给出，对表达式中各部分的数值计算方法亦有所探讨［5－6］。反问题的求解可采用最优化算法。文献［7］提出了一种基于解析法的检测金属电导率的新方法，对金属电导率实现了高精度测量；文献［8］对金属近表面电导率分布情况进行了初步反演；文献［9］针对三层平板导体在已知厚度时反推电导率，或已知电导率时反推厚度；文献［10］有效反演出了飞机发动机叶片表层涂层厚度、中间涂层厚度及电导率。

1 正问题求解及试验验证

1.1 正问题求解

如图1所示，三层不导磁无限大平板导体上方置有一空心圆柱线圈。其中，三层平板导体底层厚度为h2，电导率为σ2；中层厚度为h3，电导率为σ3；上层厚度为h4，电导率为σ4；空心圆柱线圈的内半径为R1，外半径为R2，高度为D，端部提离为H。现从空心圆柱线圈中任取一匝圆环线圈，其上面的任一点P坐标为（P′，φ，z），并将无限大空间划分为6个场区，各场区内的周向磁矢位Aφ满足以下边界条件。

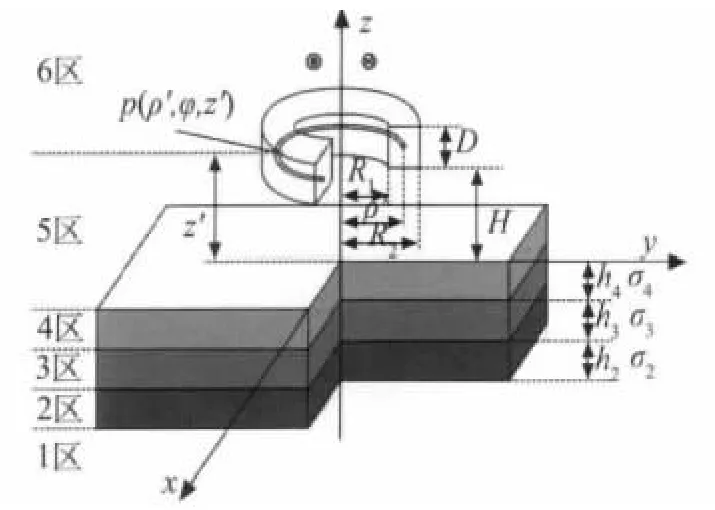
图1 三层平板导体涡流问题的求解模型

①约束方程：

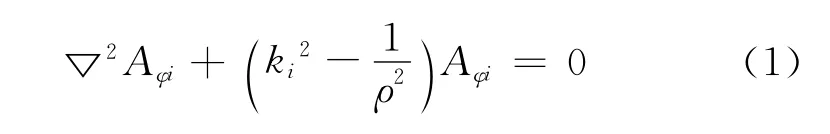
式中：i为1，2，3，4，5，6分别为0，－jωμ0σ2，－jωμ0σ3，－jωμ0σ4，0，0；μ0 为 真 空 磁导率。

②内边界上的边界条件：

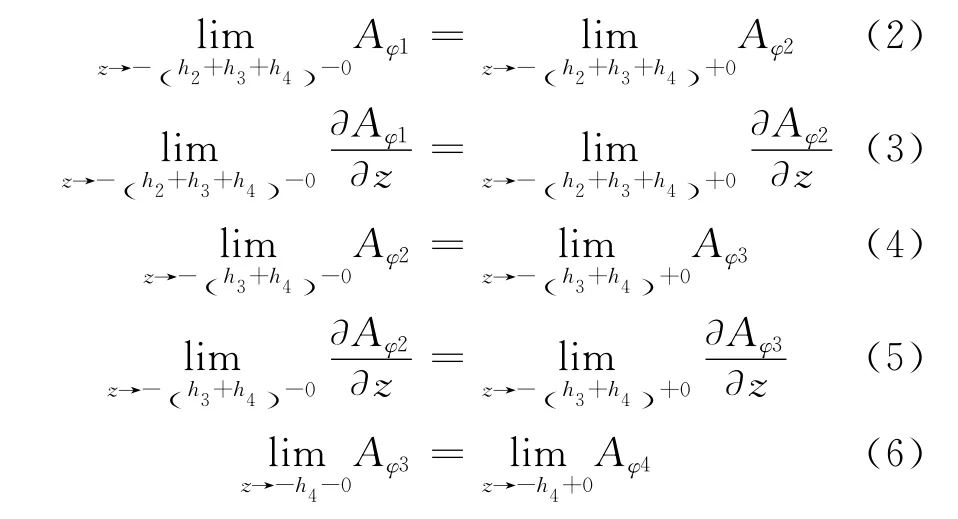
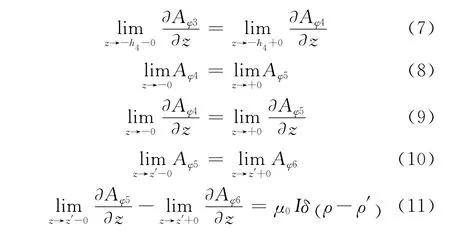
式中：z和ρ均为柱坐标系中的坐标

③无限远条件：

利用分离变量法求解约束方程（1），并结合第一类一阶贝塞尔函数J，（λρ）性质及边界条件（2）～（12）解得［2］

区别于阿斯顿·马丁旗舰车型DB11，全新Vantage兼具了造型的美感和强劲的性能。这辆颇有GT感觉的运动跑车在听觉、美学方面所成就的造诣令人向往，飞驰的快感通过莱卡（Lycra）纤维材质制成的座椅传递至驾驶者的身体，配合着高亢的发动机声线，英伦品牌独到的魅力此时被彰显得淋漓尽致。

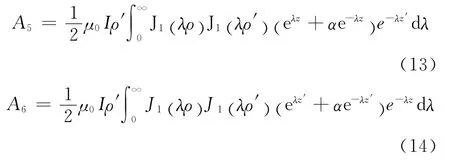
式中：λ是引入的一个参数。

其中：

在空心圆柱线圈的横截面内任选一点P，则点P所在圆环线圈平面将空心圆柱线圈分为上下两部分，仿照文献［2］中的方法将I替换为：

式中：I为电流强度；Jc为电流密度。

其中H＜z＜H＋D。进一步，根据文献［2］中给出的空心圆柱线圈两端的阻抗公式：

可得空心圆柱线圈的散射场阻抗（导体中的涡流单独作用时在线圈两端产生的阻抗）为：

式中：α为导体尺寸及电磁参数的函数。

1.2 正问题试验验证

为验证散射场阻抗表达式（17）的正确性，进行了如下试验。绕制空心圆柱线圈用作检测探头，线圈匝数43圈，内半径R1为9.95mm，外半径R2为10.20mm，高度D为3.62mm，提离H为1.20mm。取2.0mm 厚铜板，1.04mm 空气层和3.44mm厚铝板依次叠置（各层板面积不小于20cm×20cm），用以模拟3层导电不导磁平板结构。

使用游标卡尺测量各层金属板厚度（多次测量后取平均值），使用D60k型数字金属电导率测量仪测量各层金属板电导率（可测量厚度大于1.5 mm的单层金属板的电导率，测量误差小于1%）。

将线圈参数及3层平板结构各分层厚度及电导率值代入散射场阻抗表达式（17），求得散射场阻抗计算值，并与使用阻抗分析仪测量所得的测量值对比，比较结果见图2。可见，散射场阻抗计算值与测量值吻合良好。

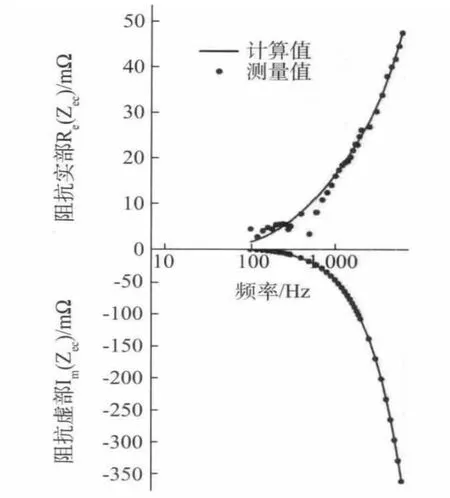
图2 空心圆柱线圈散射场阻抗计算值与测量值的对比

2 反问题计算与试验验证

2.1 反问题计算

设σ2，h2为三层平板导体底层电导率和厚度，σ3，h3为中层电导率和厚度，σ4，h4为上层电导率和厚度，σmax为待求电导率最大值，hmax为待求厚度最大值。取待测参数的向量为：

建立最优化问题如下：

其中k＝1，2，…，n；约束条件为：

设k为迭代次数，i为频率点数为频率fi处的散射场阻抗测量值为频率fi处的第k次散射场阻抗计算值。测量不同频率fi下线圈的散射场阻抗值ΔZfi，设待测参数初值为：

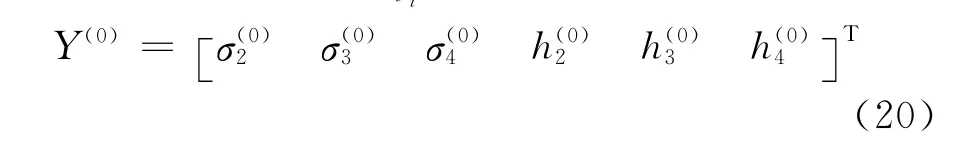
利用最优化算法［11］调整待测参数，使散射场阻抗计算值逐渐逼近散射场阻抗测量值当计算精度达到设定要求时，认为此时对应的参数值：

即为待测参数的反演值：

2.2 试验验证

为验证上述反问题的计算模型，用1.2节正问题试验验证部分的试验数据，将各频率点处的散射场阻抗试验值虚部代入反演计算程序进行计算，所得反演结果如表1所示。

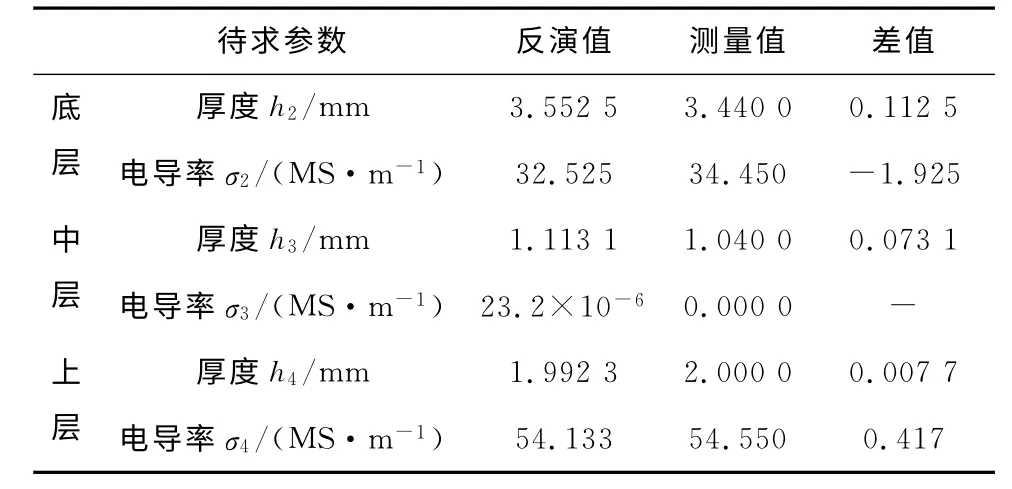
表1 反演结果

结果表明，使用上述反问题计算模型，可以在已知若干频率点的空心圆柱线圈散射场阻抗后，一次性计算出三层平板导体所有分层厚度及电导率。

3 结论

建立了三层平板导体电磁场正问题求解模型，计算导体上方空心圆柱线圈的散射场阻抗，计算值与测量值吻合良好；由激励频率范围内若干频率点处线圈散射场阻抗测量值，利用最优化方法，可一次性计算出三层导电不导磁平板结构所有分层厚度及电导率，反演结果与实际值吻合良好。

［1］ DODD C V，DEEDS W E.Analytical Solutions to Eddy－Current Probe－Coil Problems［J］.Journal of Applied Physics，1968，39（60）：2829－2838.

［2］ 雷银照.时谐电磁场解析方法［M］.北京：科学出版社，2001：178－217.

［3］ YONG LI，Theodoros Theodoulidis，GUI Yun Tian.Magnetic Field－Based Eddy－Current Modeling for Multilayered Specimens［J］.IEEE Transactions on Magnetics，2007，43（11）：4010－4015.

［4］ LENNART B.Determination of Thickness of Silver Coatings on Brass by Measuring the Impedance of a Thin Elliptic Coil［J］.IEEE Transactions on Instrumentation and Measurement，2007，56（3）：790－799.

［5］ 雷银照，马信山.涡流线圈的阻抗计算［J］.电工技术学报，1996，11（1）：17－20.

［6］ 范孟豹，黄平捷，叶波等.多层导电结构电涡流检测探头阻抗解析模型及数值计算［J］.机械工程学报，2009，45（6）：50－54.

［7］ 王新掌，雷银照.一种检测金属电导率的新方法［J］.郑州工业大学学报，2001，22（2）：62－63.

［8］ EROL U，JOHN C M，JAMES H R.Experimental determination of the near－surface conductivity profiles of metals from electromagnetic induction （eddy current）measurements［J］.Inverse Problems，1994，10：753－764.

［9］ JOHN R B，STEPHEN J N.Eddy current inversion for layered conductors［J］.Research in Nondestructive Evaluation，1992，4：205－219.

［10］ YONG LI，ZHEN Mao CHEN，YING MAO，et al.Quantitative evaluation of thermal barrier coating based on eddy current technique［J］.NDT＆E International，2012，50：1－7.

［11］ 陈宝林.最优化理论与算法（第2版）［M］.北京：清华大学出版社，2005：232－258.