铁磁材料脉冲涡流厚度检测中的边缘效应

王 健，滕永平，傅迎光，孙明璇，刘再斌，范智勇，石 坤

（1.北京交通大学 物理系，北京 100044；2.中国特种设备检测研究院，北京 100013）

脉冲涡流检测是一种新型的无损检测技术。传统的电涡流检测采用正弦电流作为激励，而脉冲涡流检测的激励电流为具有一定占空比的方波。方波包含了丰富的频谱成分，由其产生的不同频率的磁场可以到达试件的不同深度，因此可获得更多有关试件缺陷的信息［1－2］。通过脉冲涡流检测技术测量试件不同位置的厚度，可以了解试件的受腐蚀程度。对于非铁磁材料（如铝、铜等）的测厚问题国内外的研究比较多［3－6］，相应的理论也比较成熟。铁磁材料的磁导率很高，其涡流场和检测电压与非铁磁性材料有着很大的不同，测厚的特征参数也不同，国内外在这个领域的研究相对较少［7－10］。虽然文献［9－10］对铁磁材料的测厚问题进行了理论和试验研究，但在考虑被测试件时进行了理想化处理，即认为试件为无穷大。在实际测量中，有时探头会处于试件的边缘，这时用试件为无穷大模型设计出的仪器进行测厚时结果会出现误差。为了分析边缘效应对测量结果的影响，根据脉冲涡流检测的工作原理，将通过有限元方法，数值模拟探头处于被测试件边缘时，测厚误差随试件厚度和提离高度的变化关系与实验结果进行比较，再解释误差产生的原因，最后提出消除边缘效应的拟合公式。

1 脉冲涡流检测系统

脉冲涡流检测系统的基本结构如图1所示，图中的激励线圈和检测线圈组成了系统的探头。脉冲涡流检测的基本原理是：当激励脉冲加到激励线圈上时，线圈中的激励电流会产生一个脉冲磁场，这个磁场传到被测导体试件时，试件中会感应出瞬态涡流（脉冲涡流）。涡流向试件内传播且不断衰减，并产生一个快速衰减的涡流磁场。此涡流磁场又会在检测线圈上感应出随时间变化的电压。不同厚度的试件，在检测线圈上产生瞬态感应电压信号的波形是不同的。

图1 脉冲涡流检测系统基本结构

根据电磁场理论，检测线圈中的感应电压可以通过求解电磁场矢势A的微分方程［11］得到。

式中：σ、ε和μ分别为求解区域的电导率、电容率和磁导率；Js为自由电流密度。

一般情况下，方程（1）的解析解不存在，只能采用数值的方法求解。笔者使用有限元分析软件COMSOL Multiphysics 3.5a来数值求解方程（1）。

COMSOL Multiphysics是一个专业的有限元数值分析软件，只要一个物理过程可以用偏微分方程组来描述，它都能够很好地对其模拟、仿真和计算。由于它起源于Matlab的Toolbox，因而提供了与Matlab的完美接口，可将创建的模型存储为M文件，通过编辑、扩展以及执行这些M 文件以优化解决方案。对于描述脉冲涡流检测系统电磁场矢势的微分方程（1），采用如下具体的步骤求解。

1.1 建立系统仿真模型

当用脉冲涡流检测技术对导体试件的边缘进行检测时，检测系统产生的电磁场属于一个随时间变化的三维电磁场。因此，该模型应使用COMSOL Multiphysics软件AC／DC 模块下感应电流中的瞬态分析模式，并选择空间的维度为3D。根据激励线圈、检测线圈和被测导体试件的尺寸，使用绘图菜单画出它们的三维图，然后再用一个更大的边界把它们包围在内部，这样就构成了脉冲涡流检测系统的求解区域。图2就是用这种方法建立的激励线圈和检测线圈放在被测试件正上方的仿真模型。模型的具体参数为：激励线圈的内、外半径分别为20 和25mm，检测线圈的内、外半径分别为35和40mm，两线圈的高都为20mm，提离高度是30mm；被测导体试件是200 mm×200 mm 方形板，厚为20mm；边界是边长为400 mm 立方体的表面。注意：一般来讲，边界越远，求解区域越大，解的精度越高，但计算机的内存是有限的，只要把边界取的足够大，满足计算精度即可。在计算中发现：当边界离开线圈中心的距离是线圈半径的三倍以上时，计算精度就足够了。

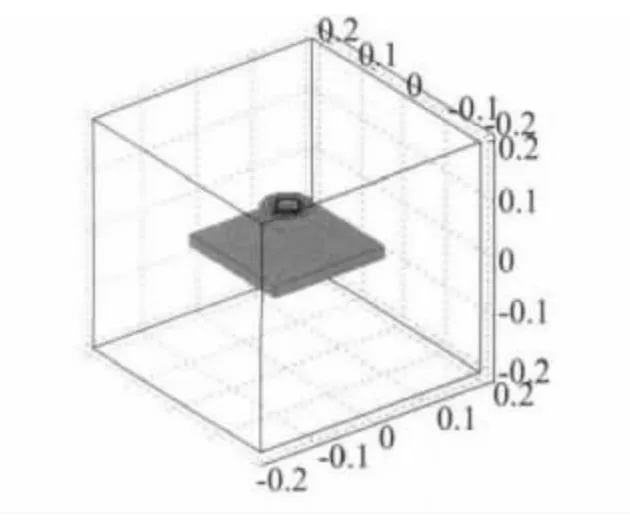
图2 脉冲涡流检测系统的仿真模型

1.2 求解域、边界、求解时间与时间步长的设定

求解域设定：求解域是边界所围成的总区域，由激励线圈、检测线圈、被测导体试件和空气4个区域构成。求解域设定指设置这些区域的电导率、相对电容率、相当磁导率和自由电流密度。各区域具体参数的取值如表1所示。

边界设定：模型的外部边界符合狄利克雷（Dirichlet）的条件，即电磁场的矢势A＝0，因此设置外部边界为磁绝缘。

求解时间与时间步长设定：试件越厚，涡流的衰减时间越长，所以试件越厚，设定的求解时间应越长。一般来讲，试件的厚度分别为10，20，30mm 左右时，求解时间分别设定为0.03，0.1，0.3s.另外，时间步长的设定也要合理，步长太短求解精度高但耗费的计算资源太多，步长太长虽节省了计算资源但求解精度低，综合考虑后时间步长设定为0.05ms。

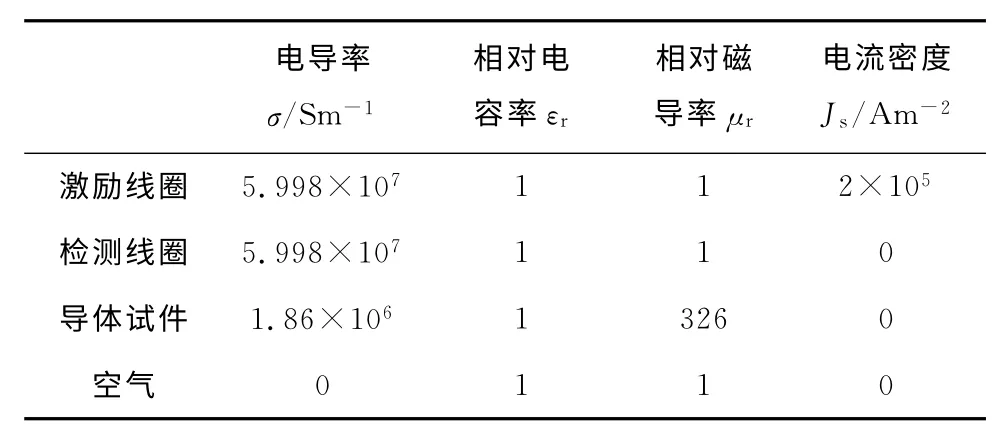
表1 各区域的电磁参数

1.3 网格划分

利用COMSOL Multiphysics网格生成器把所有区域划分成四面体单元。为了使求得的解具有较高的精度，要通过网格细化，使每个区域至少有两层以上的单元。

1.4 求解

利用COMSOL Multiphysics 求解器，即可求出区域中各时间步的电磁场矢量A。可见通过上述步骤，就实现了数值求解方程（1）的目的。

当得到矢势A（x，t）的解后，可进一步求出磁感应强度：

另外，根据电磁感应定律，得到一闭合回路L上的感应电压为：

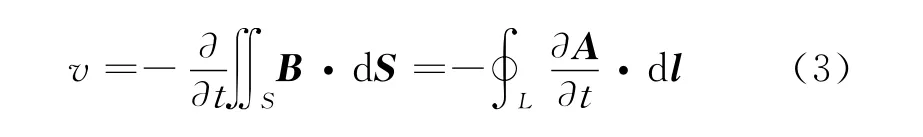
式中：S为闭合回路L所围成的曲面。

因此，检测线圈上的感应电压为：

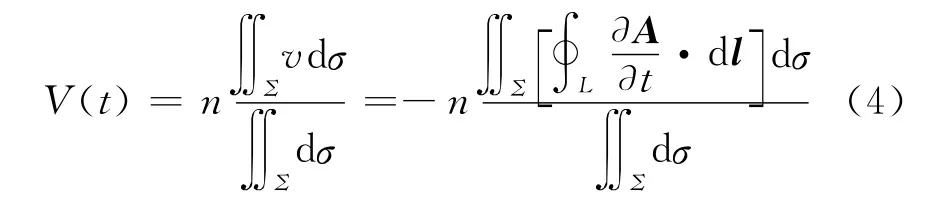
式中：n和Σ分别为检测线圈的匝数和横截面。

若建立一个x、y轴位于线圈平面内，z轴垂直于线圈平面的直角坐标系，则：

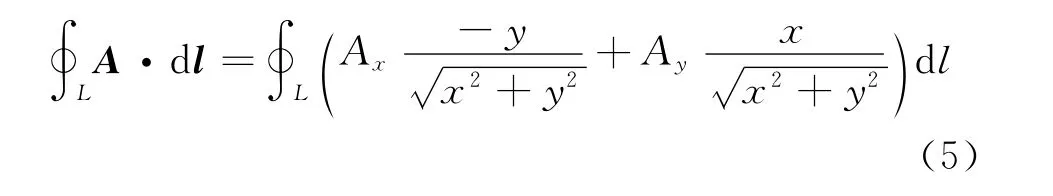
则式（4）可变为：

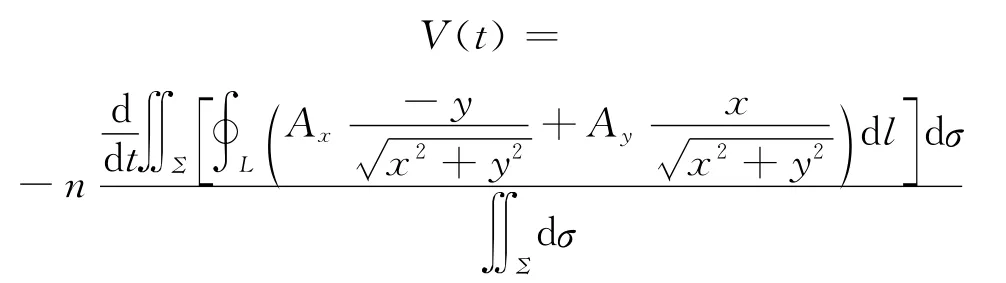
上式离散化后可为：

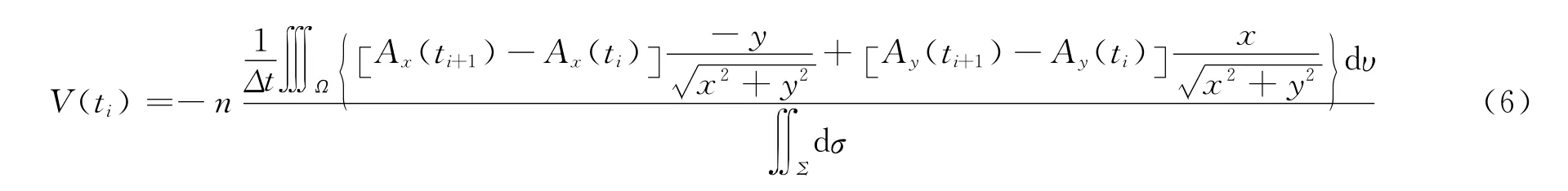
式中：ti和ti＋1分别为第i和第i＋1个时间步；Δt为时间步长；Ω为检测线圈所在的三维区域。

这样通过有限元法解出A（x，t）后，利用上式可求出脉冲涡流在检测线圈上产生的感应电压。

对于铁磁材料，其磁导率很高电导率较低，检测电压曲线与非铁磁介质有很大的不同。根据脉冲涡流检测理论，在时间和感应电压的双对数坐标系中，典型感应电压曲线如图3所示［9］。在开始一段时间内感应电压信号呈直线减小，在后面一段时间内感应电压快速衰减。图中直线部分对应着涡流从试件上表面向下表面的扩散过程，快速衰减部分对应着脉冲涡流前部到达被测试件下表面后的过程。在前面过程中，由于感应电流具有趋肤效应，涡流从试件上表面向下表面传播过程中幅度逐渐衰减，使其产生的感应电压也逐渐衰减。在后面过程中，进入试件下面空气的涡流迅速消失，涡流强度迅速变弱，所以通过涡流磁场产生的感应电压也会迅速减弱。图3中感应电压随时间的变化关系可以用公式（7）进行拟合［10］。

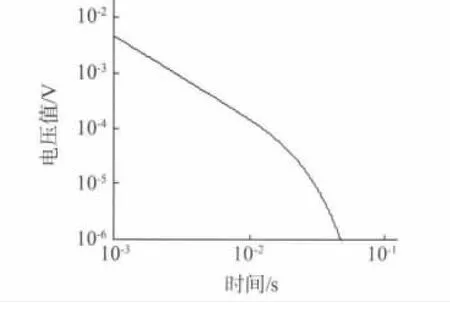
图3 典型铁磁材料的感应电压曲线

式中：A、τg和td是待定的与系统参数、被测试件参数和提离高度有关的物理量，系统参数包括激励电流幅度、激励与检测线圈尺寸和匝数等，被测试件参数包括厚度、电导率和电容率等。式中的τ为特征衰减时间。当试件为无限大平板时，τ与试件厚度的关系为：

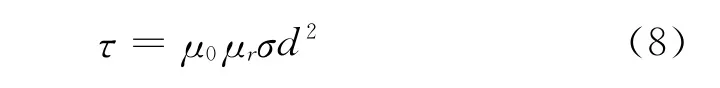
根据上述理论，对于给定的系统参数和试件参数，通过式（6）可以在理论上计算出感应电压随时间的变化规律.若系统和试件参数未知，则可通过试验测量出感应电压随时间的变化规律。最后在已知感应电压曲线的基础上用式（7）拟合出特征衰减时间τ。

当被测试件比探头大得多且探头远离试件的边缘时，可以把试件近似看成无限大平板，上述方法求出的τ满足式（8）成立的条件。脉冲涡流测厚仪器正是根据这一原理制成的，如荷兰RTD－INCOTEST 公司生产的脉冲涡流检测仪。用此仪器检测时先测量出感应电压的特征衰减曲线，再用式（7）拟合出特征衰减时间τ，然后在μr和σ已知的情况下通过式（8）获得被测试件的厚度。由于通常情况下μr和σ不容易获得，为此一般的做法是先测量标准厚度为d0的同种材料的试件，确定其特征衰减时间τ0，然后再根据被测区域的特征衰减时间，得到测量区域的厚度值。

具体公式为：

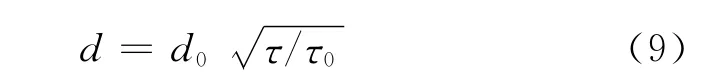
在不知道标准被测试件厚度时，也可以用二者的相对值表示，即

当探头处于被测试件的边缘时，被测试件不能被认为是无穷大的平板，以无穷大平板假设为基础的测厚仪器测量出的厚度和实际的厚度必然会存在着差别，为此主要对由于边缘效应引起的测量误差的变化规律进行分析。

2 边缘效应对测厚结果的影响

为了分析探头处于被测试件边缘时测量结果所受的影响，分别使用试验测量和数值仿真的方法进行研究。试验中使用的测量仪器是荷兰RTD－INCOTEST 公司生产的脉冲涡流检测仪，被测试件是三块500mm×500mm 的方形低碳合金钢板，厚度分别为10.5，20.3，30.5 mm。数值仿真中探头参数是根据实验中所用探头确定的，具体为：激励线圈内外半径分别为20和25 mm，匝数为400，检测线圈内外半径分别为25和30mm，匝数为1 280，两线圈的高度都为20mm。

2.1 无提离测量时的边缘效应

测量时探头底部直接与试件表面接触，为无提离测量。无提离测量情况下探头位于被测钢板试件边缘时分为两种情况，一种是放在试件的角落边，另一种情况是放在试件边缘的中间位置。

为试验无提离测量时的边缘效应，先对探头位于钢板试件厚度不同的边缘时脉冲涡流检测系统进行数值仿真。采用如下的步骤：①按本节提到的激励线圈和检测线圈的尺寸，并设500mm×500mm方形低碳合金钢板的厚度分别为6，7，8，…，29，30mm，然后让探头分别处于钢板试件的角上和钢板试件边缘的中间位置，最后用COMSOL Multiphysics软件建模，并求解不同情况下方程（1）的解，得到电磁场的矢势A（ti）；②通过式（6）求出检测线圈上的感应电压V随时间t的变化关系（感应电压曲线）；③用式（7）对感应电压曲线进行拟合，得到特征衰减时间τ；④根据μ0 ＝4π×10－7NA－2，μr＝326和σ＝1.86×106Sm－1，再用式（8）求出试件的厚度，这一厚度就是仿真得到的测量厚度。

其次，用RTD－INCOTEST 公司生产的脉冲涡流检 测 仪 对 三 块 厚 度 分 别 为10.5，20.3 和30.5mm、大小都为500mm×500mm 的方形低碳合金钢板试件进行厚度测量。在角区测得的厚度分别为：10.0，18.5和25.8mm；在边缘的中间位置测得的厚度分别为：10.1，19.5和27.9mm。

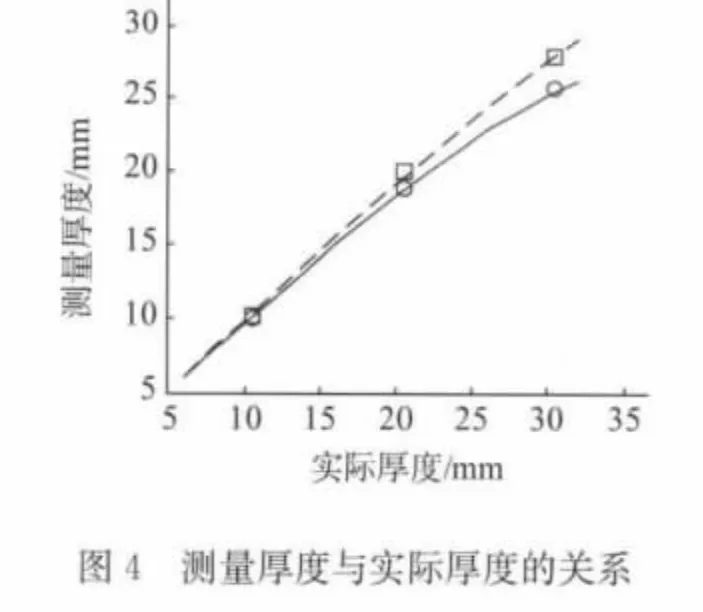
最后为了便于比较，绘出仿真测量厚度、试验测量厚度和试件的实际厚度之间的关系，结果如图4所示。其中实线是探头放在试件边角区域的仿真结果，虚线是试件边缘中间位置的仿真结果；“○”表示探头放在试件角区时脉冲涡流检测仪的测量结果，“□”表示探头放在试件一般边缘上的测量结果。

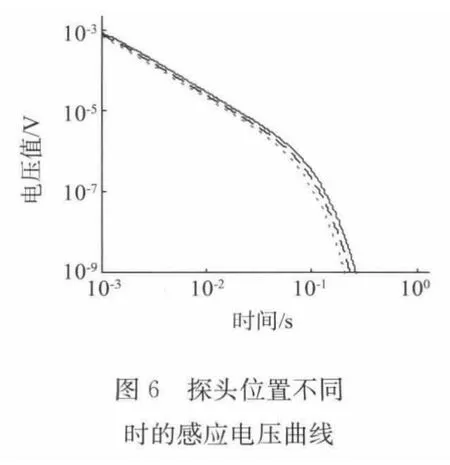
从图4可以看出：数值仿真和试验测量的一致性很好，两者都得出角区和一般边缘的测量厚度比实际厚度要小，且随着试件厚度的增大与实际厚度的相对误差也越来越大，角区的测量误差约为一般边缘误差的两倍，如图5所示，图中的实线和虚线分别表示角区和一般边缘区域的仿真测量厚度和实际厚度的相对误差。为了了解误差产生的原因，观察图6中试件厚度为20.3mm，探头分别处于试件中心（实线）、一般边缘（虚线）和角区（点线）时，检测线圈上的感应电压曲线。从此图可以看出：探头处于试件中心时，曲线最高，探头处于试件角区时，曲线最低。这主要是因为探头处于试件的角区时，涡流不但从试件的底部衰减，还可从它的两个边缘衰减，因此在检测线圈上产生的感应电压衰减较快，最终拟合出的试件的厚度也较小，造成的测量误差就比较大。

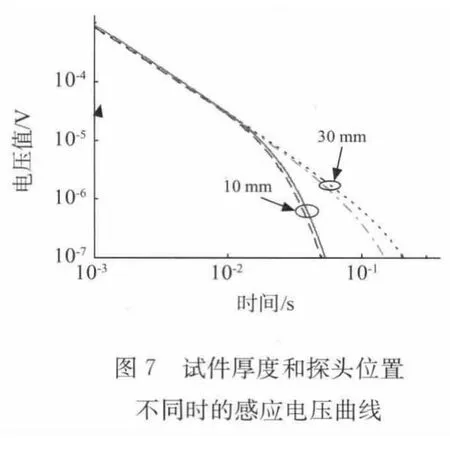
至于误差随厚度变大的原因可以从图7明显地看出，此图表示探头处于两种厚度（10和30mm）试件中心和角上时的感应电压曲线，其中实线和虚线是探头处于厚度为10mm 的试件中心和角上两种情况下的感应电压曲线，点线和点划线是探头处于厚度为30mm 的试件中心和角上两种情况下的感应电压曲线。从此图可以看出：试件越厚，探头在中心和角上两种情况下的感应电压曲线的差别也越大.这主要是因为试件越厚，涡流从试件边缘的衰减就越容易，感应电压的衰减也越快，最终得到的与试件实际厚度的差别也越大。

2.2 提离对边缘测量的影响

为了分析提离对边缘效应的影响，按照2.1的步骤，分别仿真和试验测量了探头处于厚度为10.5和20.3mm 两块方形钢板的角区，提离高度不同时的测量厚度，得到的结果如表2所示。

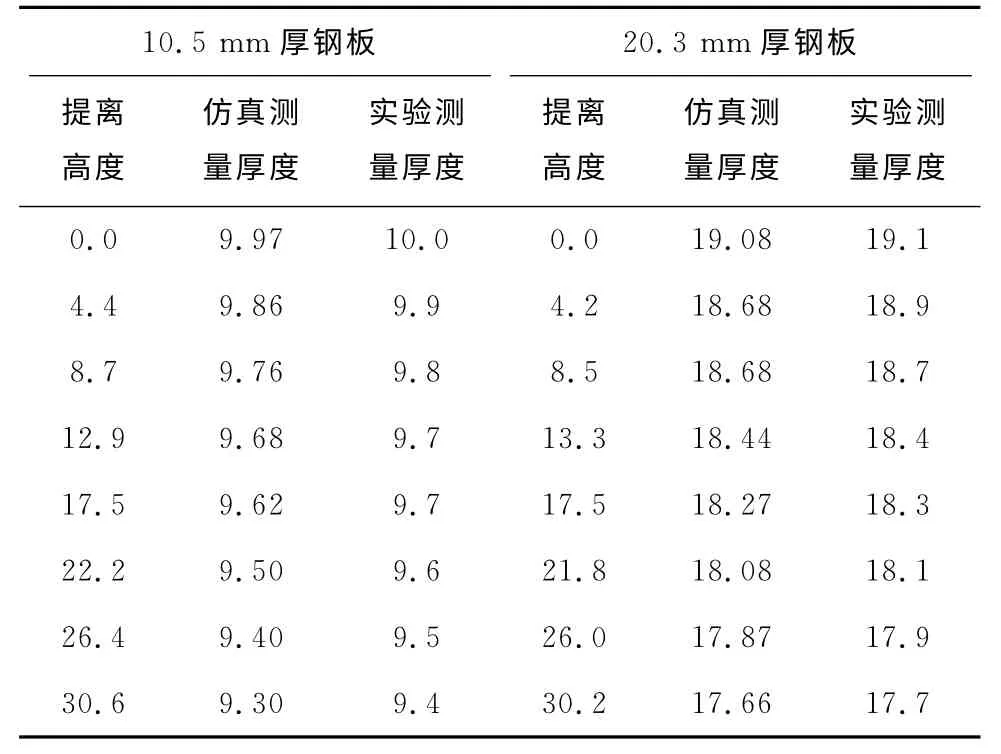
表2 提离高度不同时的仿真和实验测量厚度 mm

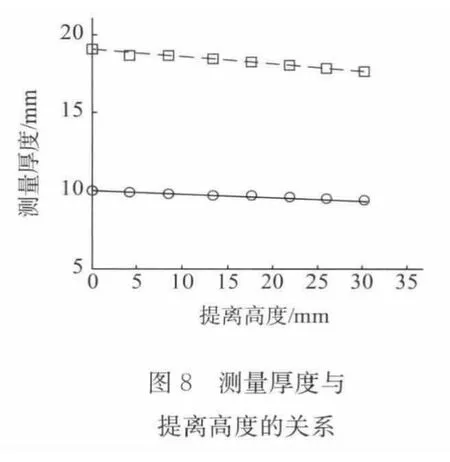
绘制了仿真和试验测量厚度随提离高度变化图，结果如图8所示。其中实线和虚线表示仿真数值，而“○”和“□”表示脉冲涡流检测仪的测量值。从此图可以看出：数值仿真和实际测量的结果基本一致，都是随着提离高度的增大，测量厚度基本上线性减小。且试件的厚度越大，提离对测量结果的影响就越明显。之所以会有这样的现象，是因为提离高度较大时，激励线圈产生的磁场在试件中的范围也大，涡流存在的区域就较大，涡流就更容易从试件的边缘衰减，从而使感应电压的曲线下降更加快速，最终使得测厚的结果变小。

2.3 消除边缘测量误差的修正公式

从2.1和2.2的结果可以看出：仿真得到的测量厚度与实验得到的测量厚度基本上是一致的，这说明使用的仿真方法是正确的，因此可以把仿真结果当成试验测量结果，来弥补试验中试件种类不足的问题。

为了得到消除边缘测量误差的修正公式，先通过数值仿真得到试件厚度和提离高度不同时的测量厚度。当探头分别处于角区和试件边缘的中间位置，实际厚度d和提离高度h不同时试件的测量厚度dm分别如表3和表4所示。

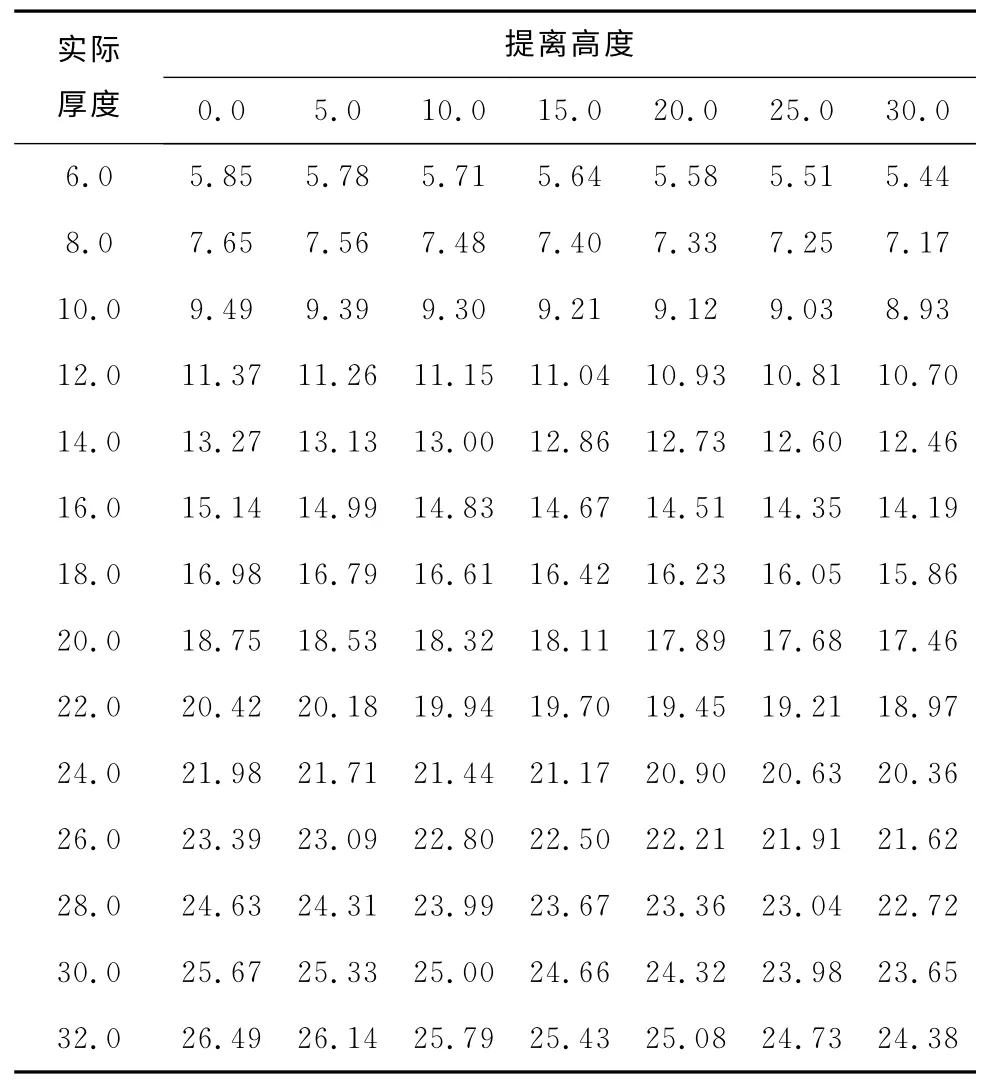
表3 探头处于角区时的测量厚度 mm

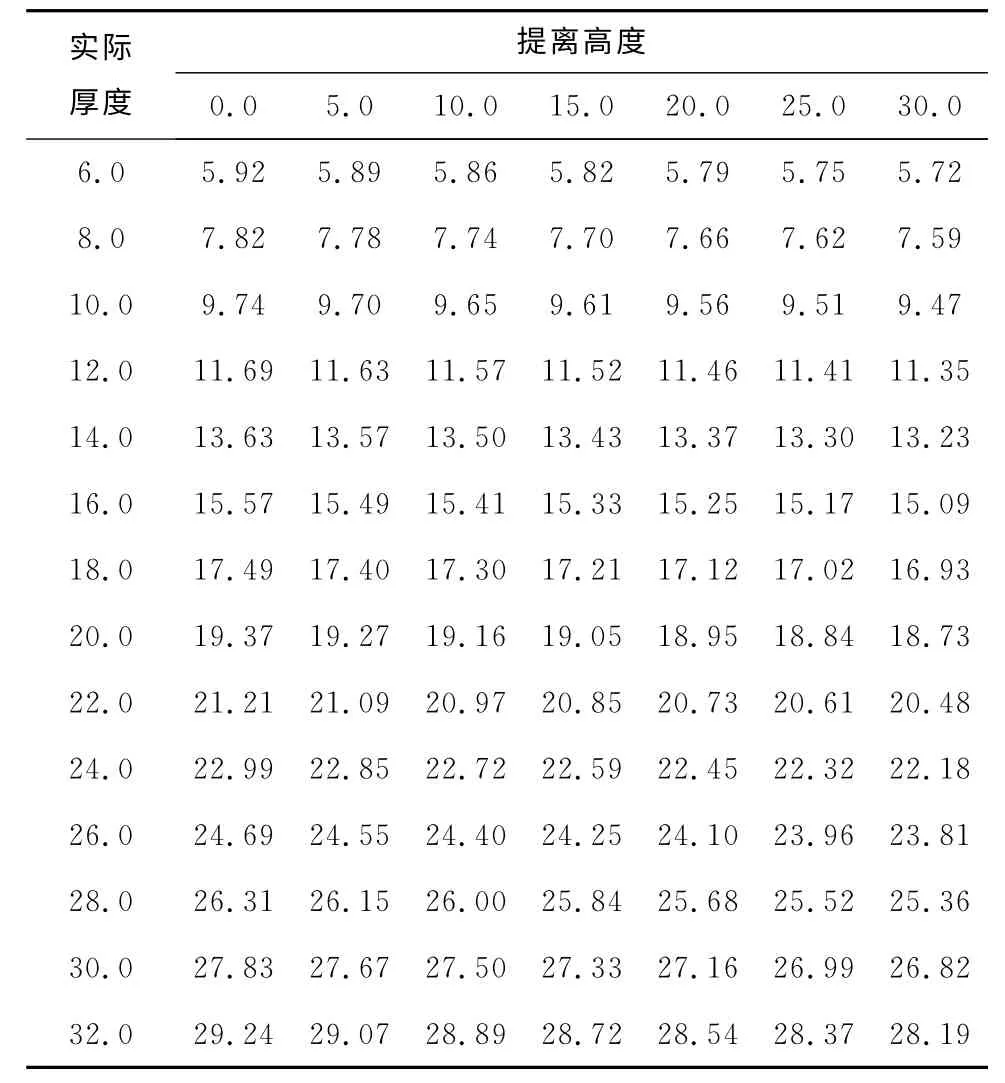
表4 探头位于试件边缘的中间位置的测量厚度 mm

根据表3的数据，使用Matlab软件，通过多项式拟合得到dm随h和d的变化关系为：

若给出dm和h的数值，求解上式，可得到d的值。利用d值随dm和h值的关系，再通过多项式拟合，最终得到探头处于角区时d与dm和h关系为：

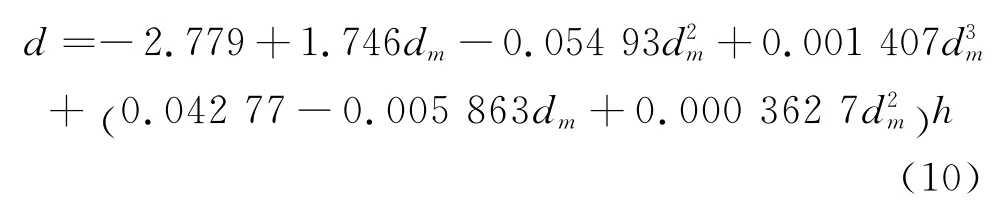
同理，利用表4，通过多项式拟合得到dm随h和d的变化关系为：

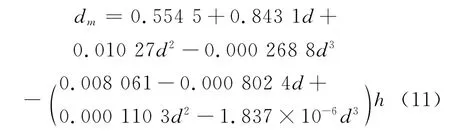
通过上式，又可以进一步得到探头处于远离角区的一般边缘时d与dm和h关系为：

公式（10）和（12）即为消除边缘测量误差的修正公式。在实际操作中，试件的实际厚度d是需要测量的，而仪器的测量结果dm又有误差，但可以把dm和相应的提离高度值h，代入公式（10）或（12），就可得到试件的实际厚度d，这样就达到了消除边缘测量误差的目的。应该注意的是：以上两个拟合公式中dm和h的范围分别为7～30mm，0～30mm。

3 结论

脉冲涡流测厚可以检测铁磁材料的受腐蚀程度，然而脉冲涡流检测仪的测量原理是建立在被测试件比探头大得多且探头远离边缘的基础之上的。当探头处于试件的边缘时，测量结果会受到影响。在脉冲涡流检测原理的基础上，通过数值仿真和实验测量分析了探头处于边缘不同位置时，试件厚度和提离高度对测量结果的影响。试验表明：探头处于试件的边缘时，测量厚度总比试件的实际厚度小；试件厚度和提离高度越大，测厚的误差也越大；探头处于试件角区比处于远离角区的一般边缘，测量误差要大一倍左右。为了减少边缘效应引起的测量误差，最后给出探头处于角区和一般边缘时，用测量厚度和提离高度计算试件实际厚度的拟合公式。相信这些结果会对脉冲涡流的实际检测有一定指导意义。

［1］ SMITH R A，HUGO G R.Transient eddy current NDE for ageing aircraft－capabilities and limitations［J］.Insight，2001，43（1）：14－25.

［2］ GIGUÈRE S，LEPINE B A，DUBOIS J M S.Pulsed eddy current technology：characterizing material loss with gap and lift－off variations［J］.Research in Nondestructive Evaluation，2001，13（3）：119－129.

［3］ BOWLER J，JOHNSON M.Pulsed eddy－current response to a conducting half－space［J］.IEEE Transactions on Magnetics，1997，33（3）：2258－2264.

［4］ SOPHIAN A，TIAN G Y，TAYLOR D，et al.A feature extraction technique based on principal component analysis for pulsed eddy current NDT［J］.NDT ＆ E International，2003，36（1）：37－41.

［5］ 郑岗，赵亮.金属厚度的脉冲涡流无损检测研究［J］.传感器与微系统，2006，25（4）：35－40.

［6］ 徐平，罗飞路.多层金属结构腐蚀缺陷脉冲涡流检测技术研究［J］.动化仪表，2007，28（11）：25－28.

［7］ 吴鑫，李方奇，石坤，等.脉冲涡流测厚技术理论与应用［J］.北京交通大学学报，2009，33（1）：20－23，31.

［8］ 武新军，黄琛，丁旭，等.钢腐蚀脉冲涡流检测系统的研制与应用［J］.无损检测，2010，32（2）：127－130.

［9］ HAAN V O，JONG P A.Analytical expressions for transient induction voltage in a receiving coil due to a coaxial transmitting coil over a conducting plate［J］.IEEE Transactions on Magnetics，2004，40（2）：371－378.

［10］ HAAN V O，JONG P A，PEREZ L，et al.Towards material characterization and thickness measurements using pulsed eddy currents implemented with an improved giant magneto resistance magnetometer［J／OL］.ECNDT，2006，We.2.6.4

［11］ DAI X W，LUDWING R，PALANISAMY R.Numerical simulation of pulsed eddy－current nondestructive testing phenomena［J］.IEEE Transactions on Magnetics，1990，26（6）：3089－3096.