完全偶图的定向图

张雪飞，王世英

(山西大学数学科学学院，山西太原030006)

1 引言

给定任意图G，对于它的每条边，给其端点指定一个顺序，从而确定一条弧，由此得到一个有向图。这样的有向图称为G的一个定向图。Buhler等［1］研究了超立方体的定向图D，满足D中的顶点的入度是a或者是b，证明了这样的定向图存在的充分必要条件是存在两个非负整数s和t使得s+t=2n且as+bt=n2n－1。用(a，b)n表示n维超立方体H可以定向，使得它的顶点的入度是a或者是b，并称H是(a，b)n可实现的。上面的结果可以重新叙述如下:设n为正整数，a，b∈{0，1，2，…，n}，(a，b)n可实现当且仅当存在非负整数s和t，满足下面两个方程:

其中方程(1)是关于超立方体的顶点数的，方程(2)是关于超立方体的边数的。

上述结果的必要性是明显的，事实上通过计算超立方体的顶点和边数就可以得到。但是在充分性的证明中利用了源放入理论［2］，以致并不是所有图都可以定向，满足定向图的顶点的入度是a或者是b。

每一对不同的顶点都有一条边相连的简单图称为完全图。偶图(或二部图)是指一个图，它的顶点集可以分解为两个非空子集X和Y，使得每一条边都有一个端点在X中，另一个端点在Y中，这样一种二分类(X，Y)称为图的一个二分类。完全偶图是具有二分类(X，Y)的简单偶图，其中X的每个顶点与Y的每个顶点相连，若|X|=m，|Y|=n，则这样的图记为Km，n。对于二部图的研究得到了广泛的关注，如文［3］。

对于一条弧(u，v)，称顶点u控制顶点v，记为u→v。称u是弧(u，v)的尾，v是弧(u，v)的头。对有向图D的两个不相交的顶点子集X和Y，X→Y表示X中的每一个顶点控制Y中的每一个顶点。有向图D中顶点v的入度d-D(v)是指以v为头的弧的数目，在没有混淆的情况下把d-D(v)写成d-(v)。

图G的一条途径是指一个有限非空序列W=v0e1v1…ekvk，它的项交替地为顶点和边，使得对1≤i≤k，ei的端点是vi－1和vi，称W是从v0到vk的一条途径。若途径W的边e1，e2，…，ek互不相同，则W称为迹。经过图G的每条边的迹称为G的Euler迹。图G的环游是指经过G的每条边至少一次的闭途径。经过每条边恰好一次的环游为Euler环游。换言之，Euler环游是闭Euler迹。一个图若包含Euler环游，则这个图称为Euler图。

设a，b为整数且b≠0，用b|a表示b整除a。

引理1［4］一个非空连通图是Euler图当且仅当它没有奇点。

引理2［5］如果素数 p|ab，则 p|a或p|b。

本文研究Kn，n的定向图D，满足D中每个顶点的入度为a或者为b。为了简便起见，用［a，b］n表示把Kn，n定向为有向图D，使得D 中顶点的入度是 a或者是 b的一个图类，并称 Kn，n是［a，b］n可实现的，简称［a，b］n是可实现的。文中其它未定义的图论术语和记号参见文献［4，6］。

2 主要结果

定理1 设 n 为正整数，a，b∈{0，1，2…n}，若 Kn，n是［a，b］n可实现的，则存在非负整数 s和 t，满足下面两个方程:

证明 由于Kn，n是［a，b］n可实现的，因此存在Kn，n的一个定向图D使得每个顶点的入度是a或者是b。设D中入度为a的顶点个数为s。注意到D中所有顶点入度的和为n2。我们有sa+(2n－s)b=n2，令t=2n－s，此时s和t为满足方程(3)和(4)的非负整数。证毕。

如果 n 为正整数，a，b∈{0，1，2，…，n}，则有以下命题成立。

命题1 (1)若［a，b］n是可实现的，则［n－a，n－b］n是可实现的。

(2)［0，n］n是可实现的。

证明 (1)当［a，b］n可实现时，则Kn，n中每个顶点的入度是a或者是b，把Kn，n中所有弧的方向调换，即原来弧的始点变为终点，终点变为始点，又因为Kn，n是n正则的，所以后来得到的有向图D的每个顶点的入度是n－a或者n－b。

(2)在二部图Kn，n中，它有一个二分类(X，Y)，且|X|=n，|Y|=n，我们给其一种特殊的定向，使得X→Y，则X中n个顶点的入度为0，Y中n个顶点的入度为n，因此［0，n］n是可实现的。

表1 ［a，b］n的数据表Table 1 The datasheet of［a，b］n

通过观察这些数据，发现它们有一定的规律可循。特别地，K1，1中只有一条边，把该边定向后，弧的两个端点中一个入度为0，一个入度为1，显然［0，1］1是可实现的，以下假设n≥2。

定理 2 设 a，b，s，t为非负整数(a，b∈{0，1，2，…，n})满足下面两个方程:

则在Kn，n中有以下结论成立:

(1)若 n为素数时，则［a，b］n是可实现的，其中 b=n－a。

(2)若 n为合数且满足 s≥a，n－s≥b和 n+≥2b，则［a，b］n是可实现的。

证明 (1)当n为素数时，a≠b，设 a＜b。由方程组(3)，(4)可得 a(2n－t)+bt=n2，整理后得到(b－a)t=n(n－2a)。因为a，b∈{0，1，2，…，n}，a＜b，且 n为素数，故 n|(b－a)t。又因为 0 ＜b－ a≤n，当b－a=n时，a=0，b=n，可知s=n，t=n。当0 ＜b－a＜n时，n|(b－a)，由引理2 可知n|t。同理可知n|s。又因为s+t=2n，且s，t为非负整数，故得到s=t=n。当s=t=n时，可求解出b=n－a。故由方程组仅可求出的解为［a，n－a］n。下证［a，n－a］n是可实现的。

在 Kn，n中，它有一个二分类(X，Y)，且|X|=n，|Y|=n，X 中的顶点表示为 ui，Y 中的顶点表示为 vj，i，j∈{1，2，…，n}。

对X中任意顶点ui，令v(i+l)(mods)→ui，其中l=0，1，…，a－1。对 Y中的其他顶点 vk，定向 vk与 ui间的弧为ui→vk。这样集合X中n个顶点的入度为a，集合Y中n顶点的入度为n－a，故证得［a，n－a］n是可实现的。

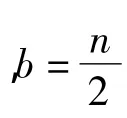
对 X1中任意顶点 ui，令 v(i+l)(mods)→ui，其中l=0，1，…，a －1。对 Y1中的其他顶点 vk，定向 vk与 ui间的弧为ui→vk，且X1中的顶点控制Y2中的顶点，即X1→Y2。同理，对X2中任意顶点uj，令v(j+l)→uj，其中l=0，1，…，b－1，且当 j+l＞n时，令 v(j+l)=v(j+l)(modn)+s。对 Y2中的其他顶点 vm，定向 vm与 uj间的弧为 uj→um，且X2中的顶点控制Y1中的顶点，即X2→Y1。

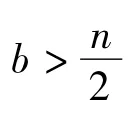
下面对Y中顶点的入度进行调整，对Y2中任意满足d-(vl)=n－b＜b的顶点vl，在X2中存在某个顶点uj，使得 ul→uj。任取 uk∈Y1，则 uj→vk。转换 vl→uj→vk为 vk→uj→vl。该过程中 vk的入度数减少 1，vl的入度增加1，uj的入度不变。若d-(vl)+1仍然小于b，注意到vl在X2中的外邻集中的点数为b，在X2中存在某个顶点 uj'，使得 uj'≠uj并且 vl→uj'。选取 uk'∈Y1，使得 d-(vk')＞ b，则 uj'→vk。转换 vl→uj'→vk'为 vk'→uj'→vl。该过程中 vk'的入度减少1，vl的入度增加1，uj'的入度不变。注意到 n+s≥2b，我们有 s(n－s)≥［b－(n－b)］(n－s)。将上述过程一直进行下去，直到 d-(vl)=b。由 vl的任意性以及(n－a－b)s=(b－(n－b))(n－s)，可知上述过程结束时Y1中的所有顶点的入度均为b。此时［a，b］n是可实现的。证毕。

［1］BUHLER J，BUTLER S，GRAHAM R，et al.Hypercube orientations with only two in-degrees［J］.Journal of Combinatorial Theory，Series A，2011，118(6):1695-1702.

［2］BUTLER S，HAJIAGHAYI M T，KLEINBERG R D，et al.Hat guessing games［J］.SIAM Journal on Discrete Mathematics，2008，22(2):592-605.

［3］高敬振，邵光凤.极大局部边连通和超级局部边连通二部有向图的邻域条件［J］.山东科学，2012，25(2):1-7.

［4］BONDY J A，MURTY U S R.Graph Theory［M］.New York:Springer，2008.

［5］聂灵沼，丁石孙.代数学引论［M］.北京:高等教育出版社，2009.

［6］JENSEN J B，GUTIN G.Digraphs Theory，Algorithms and Applications［M］.New York:Springer，2007.