成网条件下城市轨道交通车底运用问题研究

李洁，何世伟，何必胜

(北京交通大学交通运输学院，北京100044)

为缓解日益严重的城市交通拥堵问题，我国一些特大城市大力开展轨道交通建设，在较短时期内由单一线路形成网络。由于路网规模的快速扩大，原有的单线运营管理模式不能完全适应网络化运营，迫切要求研究新方法以应对这种快速变化的新局面。成网条件，即总控制中心负责多条线路的运行控制和协调调度，线路采用相同类型的信号系统和供电制式，更新的车辆及运营设备类型保持统一和兼容，可实现维修、配件和技术资源的充分共享。而城市轨道车辆价格昂贵，在固定设备投资中占较大比重，车底运用计划又是城市轨道交通运营规划中重要的内容之一，因此运营效益最大化要求投入适当数量的车辆，合理地安排列车接续和检修，缩短列车非生产时间，提高利用率，降低运营成本。

轨道交通运营问题一直是国内外学者研究的重点内容。Tomoshi Otsuki等［1］将机车车辆配置问题定义为多商品流问题，并提出基于搜索的启发式算法。Luis Cadarso等［2］分析了在发车频率高、站间距短的快速公交网络中，建立模型解决不同线路间的能力与车辆共享问题。王彦栋［3］建立了以接续时间和维修时间最少为目标函数的车底运用计划模型。缪道平［4］分别从车底使用数量最少和均衡性最好的角度建立模型。徐瑞华等［5］提出“运行图周期分析法”，建立多种交路条件下城市轨道交通通过能力和车底数量的数学模型。吴涛［6］推演出共线运行图不同行车间隔时间条件下的运行图周期和车底运用列数的计算方法。陶志祥［7］从客流特征、运营管理、基础设施及设备兼容等方面分析了区域城际铁路与城市轨道交通跨线运行的兼容性。可见，国外的研究工作主要集中在列车的编组方案、通过能力等方面，以灵活的编组结合对行车密度的调节来适应不同时期和不同时段客流量变化的要求，虽然研究较成熟，但不符合我国城市轨道交通固定编组的情况，不能直接应用，但其建模思路与方法可作为借鉴经验。而我国城市轨道交通大多以单线运营为基础，研究多以单线路条件为背景，或以成网条件下的客流情况和运输能力为研究方向，较少涉及到成网条件下的车底运用计划。

本文给出成网条件下城市轨道交通车底运用问题的优化方法，即基于网络流模型的单车场与多车场车底运用模型，以构建最优任务序列(即行车计划)，节省车底使用数，降低运营成本。最后采用ILOG CPLEX 12.5优化软件，结合算例对模型求解分析，并与启发式算法进行了比较，验证了求解方法的高效性。

1 成网条件下城市轨道交通车底运用问题研究

1.1 问题描述

城市轨道交通车底运用问题可以描述为:给定时刻表等相关信息，在满足相关约束条件下，调度车辆执行时刻表给定任务(中间可插入空驶班次以减少车辆需求)，使每一任务均有唯一车辆执行，从而构建车辆执行的任务序列(行车计划)。其最主要的优化目标是在现有车辆水平下安排车辆调度方案使运用车辆数或费用最少。

与公交可灵活地进行区域调度不同，城市轨道车辆只能在既定轨道上行驶，交路形式略显单一，可以从公交的行车计划编制中汲取经验。为研究城市轨道交通车底运用问题从单线向网络化运营的变化情况，本文以单车场车底运用问题和多车场车底运用问题为理论基础。

单车场车底运用问题指一条线路只配备有一个车场，该线路上的所有收发车任务均由此车场的车底完成。我国多数城市的轨道交通路网为单线叠加而成，这种调度方案可以很好的满足客流成网的运营组织需求，而且组织模式简单，易于操作，稳定性强。针对单车场车底运用问题，提出最小总成本的优化目标和约束条件。

随着轨道交通的迅速发展，路网不断升级，车场建设增多，线路间联系紧密，单车场车底运用模式转变为多车场车底运用模式，包含以下两种情况:(1)一条线路配备多个车场，即单线路多车场;(2)每条线路配备车场不唯一，可以实现车辆在线路间的跨线运营，即多线路多车场。多车场车底运用模式研究解决区域内多个场站的车辆整合调度问题，指定最佳的执行车辆(分布于多个车场)使区域内所需的车辆数最少。

成网条件下的城市轨道交通车底运用问题涉及单车场和多车场两种情况，需根据线路和车场的具体形式进行具体分析。

1.2 网络构建与符号描述

n∈N表示任务集合;rk∈R表示出发车场节点集合，tk∈T表示到达车场节点集合;Vk=N∪R∪T为车场中节点集合;A={r×N，N×t}为单车场中弧段集合，Ak={rk×N，N×tk}为多车场中弧段集合。

车底调度网络可以定义为:单车场时有网络 G=(V，A)，多车场时对每一车场 k∈K有网络Gk∈(Vk，Ak)。其中，该网络中从r到t路径表示一辆车的可行调度方案。可行调度方案集合就是能覆盖所有任务的从r到t的路径集合。

m∈M表示单车场中的车辆集合，m∈Mk表示车场k的车辆集合;

cij表示连接弧(i，j)∈A的成本，一般设置为行程时间(不包括车次任务时间)，本文中以秒为计量单位;对于(i，j)∈N驶出驶入车场的弧段(r，i)(j，t)，其成本为车辆使用的固定成本，换算为秒计量;

tij表示连接任务i，j的最小折返时间，此处指同一车站的折返时间;

nij表示连接任务i，j的列车编组数;

l为所用车辆长度;

Lij为任务i，j所在线路上的最小站台长度;

ymij为单车场车底运用模型的0-1决策变量，ykmij为多车场车底运用模型的0-1决策变量，表示第m辆车在完成了任务i后是否接续任务j。

1.3 建立模型

构造单车场车底运用网络G。

图1中，节点包括任务节点(任务a、任务b、任务c、任务d，如表1所示)和车场节点(分别用r，t代表起始点和终止点)。(a，b)，(a，c)，(a，d)，(b，c)(b，d)，(c，d)为 6 条连接弧，其余为车场驶入驶出弧。具体假设该车场存在3辆车。路径r-a-c-t即为1辆车的调度方案，而r-a-c-t和r-b-d-t组成的路径集合即为一可行调度方案。该可行的调度方案对应的决策变量值如下:y1ra=1，y1ac=1，y1ct=1，y2rb=1，y2bd=1，y2dt=1，第 3 辆车空闲。

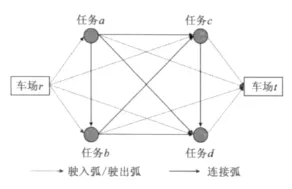
图1 单车场车底运用网络Fig.1 Single-depot rolling stock assignment network

表1 任务时间表Table 1 Task scheduling table

单车场车底运用模型如下:

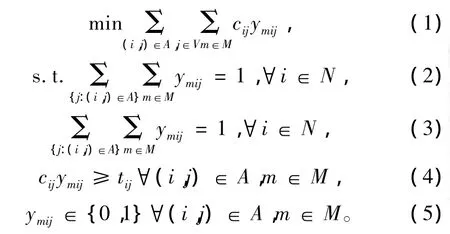
式(1)表示成本最小;约束(2)，(3)表示每一任务都必须被一辆车完成;约束(4)表示连接的两任务间要满足最小折返时间;约束(5)为变量约束。

构造多车场车底运用网络，如图2所示。

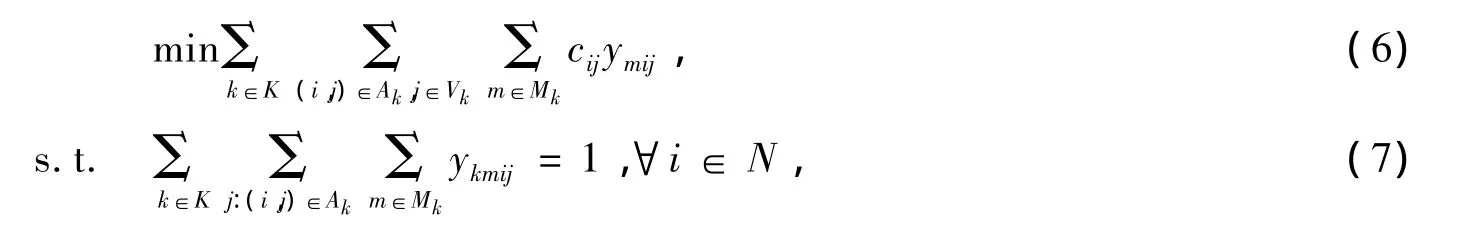
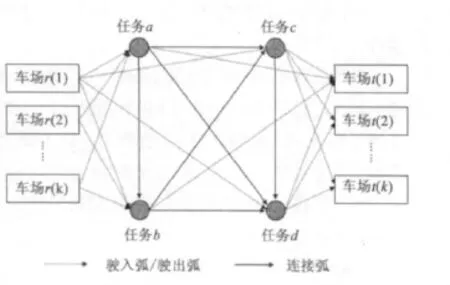
图2 多车场车底运用网络Fig.2 Multi-depot rolling stock assignment network

式(6)表示成本最小;约束(7)保证每一任务由一辆车完成;约束(8)流量守恒约束;约束(9)表示连接的两任务要满足最小折返时间;约束(10)表示完成i，j任务的列车长度应符合站台长度要求;约束(11)为变量约束。

在实际调度过程中，很多车场要求车辆回归本段停放，即车辆从哪个车场出发，结束任务后必须回到原始车场，这样就方便了车辆的管理与维修。其中约束(8)在保证流量守恒的同时，也要求车辆回段，该约束对模型的影响将在后文中进一步分析。

车场调度问题的求解方法主要有以下3类:精确算法、启发式方法以及模拟方法。本文选择ILOG CPLEX 12.5作为求解方法，ILOG CPLEX 12.5提供灵活的高性能优化程序，在应用程序开发和部署过程中，开发者可以使用多种不同的方法与ILOG CPLEX 12.5进行交互，即可以通过大多数编程环境来访问ILOG CPLEX 12.5，并在多个平台上对其进行使用，实现了可移植性，多用于模拟实际问题。同时，本文还将免疫克隆算法作为对比算法，此算法相比于其他智能优化算法，具有克隆、超变异、免疫记忆等特色功能，而且收敛速度快、易于编程实现，在保证收敛速度的同时又能维持抗体的多样性，算法参见文献［8］。但是该算法迭代后期容易出现停滞现象，导致搜索精度不高，对初始解有较强的依赖性，容易陷入局部最优。当数据规模较小时，ILOG CPLEX 12.5收敛速度快;当规模较大时，收敛速度慢，可能会出现内存溢出现象，无法获得可行解。

2 算例分析

2.1 案例背景

本研究选取上海地铁2号线与7号线为例进行分析计算。表2为案例分析所涉及的参数。

表2 参数介绍Table 2 Parameter introduction

各停车场及车辆段位置如图3所示。

每条线路开通初期，两车场并非同时投入运营，建设时间有先后，在第2个车场投入使用前，单线路车底运用问题可由单车场模型解决。随着2号线与7号线的其余车场建成投用后，形成多车场局面。龙阳路停车场共同用于2号线与7号线列车的停放与养护，但是两条线路车辆仍然独立使用，未形成网络化运营。假设将来随着客流量的不断增多，7号线扩大为8节编组，两条线路统一调度，即可实现车辆的跨线行驶。川沙停车场主要用于4节编组的列车停放，在广兰路站以西形成一个拥有3个车场、两条线路的小型区域网络，以此为研究对象展开进一步分析。

2.2 计算结果

以列车间隔为基础，选取周一至周四的早高峰时段(7:00～9:00)，编制行车计划表，将所有车次的任务按照发车时间先后顺序从1开始排列，利用ILOG CPLEX 12.5软件输出任务序列和总成本费用。不考虑折返线数量的限制。

(1)2号线独立运营(图4)。选取两个车场:北翟路车辆段、龙阳路停车场，两个车站:广兰路站、淞虹路站，为单线路多车场，符合多车场车底运用模型。计算得总成本费用为14 472 s(即连接弧的时间费用总和，由于任务固定，故未包括车底执行车次过程的时间费用，下面计算方法相同)，使用车辆25列。

(2)7号线独立运营(图5)。选取2个车场:陈太路停车场、龙阳路停车场，2个车站:上海大学站、花木路站，为单线路多车场，符合多车场车底运用模型。计算得总成本费用为11 040 s，使用车辆32列。

(3)网络化运营(图6)。选取3个车场:北翟路车辆段、陈太路停车场、龙阳路停车场，4个车站:上海大学站、花木路站、广兰路站、淞虹路站，为多线路多车场，符合多车场车底运用模型。计算得总成本费用为22 512 s，使用车辆55列。

图3 二号线及七号线停车场及车辆段位置示意图Fig.3 Illustration of parking lot and depot location for lines 2 and 7

图6 实行网络化运营后列车运行图Fig.6 Train timetable for transit network

2.3 结果分析

通过3组数据的对比可以看出，当实现2号线与7号线的跨线运营后，总成本费用相对于两线独立运营的成本费用之和降低了近12%，运用总车辆数也同时减少。城市轨道交通车辆价格昂贵，这样一来大大减少了投资成本与维修费用，可将节省的列车当作备用车辆，有积极的现实意义。这说明成网条件下，车底资源得到了有效配置，达到预期目标。

若执行完一天的开行计划后要求车辆回归本段停放，增加这一约束，重新求解得到另一组数据，见表3。

表3 车辆是否回归本段运算结果Table 3 Results of entering a depot or not

从表3中可以看出，当要求车辆回归本段停放时，得到的总成本费用大于或等于第一组数据，这是因为车辆执行完所有载客任务后，部分车辆必须空驶回原始车场，增加了一部分费用。从结果来看，总体上该约束对任务节点的接续情况影响不大。若车型相同，只要尽量保证各车场车辆数的均衡，以便顺利执行开行方案，即可在完成所有任务后，车辆不要求回到原始车辆段，从而减少空驶。

本文采取免疫克隆算法与软件ILOG CPLEX 12.5对模型进行求解，最终求解结果中的总成本费用与使用车辆数二者保持一致，但免疫克隆算法求解模型的平均运行时间为5.1 s，平均迭代次数为227次，而ILOG CPLEX 12.5平均运行时间为1.59 s，平均迭代次数75次。两种算法的求解关系迭代图如图7所示。当求解数据规模较小时，相比于免疫克隆算法，ILOG CPLEX 12.5在求解模型上运行时间更短，收敛性更强，验证了ILOG CPLEX 12.5求解模型的高效性。

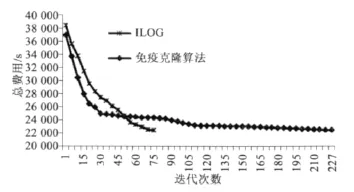
图7 ILOG与免疫克隆算法求解模型关系曲线Fig.7 Relationship curves of the solution model of ILOG and immune clone algorithms

当数据规模较大时，再运用ILOG CPLEX 12.5与免疫克隆算法进行求解，得到表4所示对比结果。当任务数由130变为204时，ILOG的求解时间仍然低于免疫克隆算法。任务数扩大到292时，ILOG求解时间明显增大，再增至460时求解时间已经达到16 832.7 s，远远超过免疫克隆算法的19.0 s。而执行全天的896个任务时，免疫克隆算法只需37.4 s，ILOG虽能获得可行解，但求解时间太长，效率较低，当线路增加任务数更多时，该方法不可行。由此可见，ILOG CPLEX 12.5虽然能获得优化解，但是随着问题规模的扩大，其求解速度变慢，免疫克隆算法求解质量相对差一些，却能有相对较快的求解速度。因此，在实际的生产工作中，应该将ILOG CPLEX 12.5与免疫克隆算法配合使用，当对计算的求解质量要求较高时，采用ILOG CPLEX 12.5，而对时效性要求较高时，选择免疫克隆算法。

3 结论

本文主要研究了成网条件下城市轨道交通车底运用问题。随着地铁网络化的发展，单车场调度模型存在一定的局限性，在此基础上构建了多车场调度模型，建立了使总成本费用最少的目标函数，约束中考虑了折返时间、站台长度等现实条件，并新增是否回场的约束。采用ILOG CPLEX 12.5和免疫克隆算法对该问题进行了求解分析，并结合算例验证了模型和求解方法的有效性，为成网条件下的城轨车底运用问题提供了较好的决策参考依据。

［1］OTSUKI T，AISU H，TANAKA T.A search-based approach to the railway rolling stock allocation problem［J］.Lecture Notes in Computer Science，2010，6509:131-143.

［2］CADARSO L，MARIN Á .Robust rolling stock in rapid transit networks［J］.Computers and Operations Research，2011，38(8):1131-1142.

［3］彦栋.城市轨道交通车体运用计划编制模型研究［J］.物流技术，2011，30(12):98-100.

［4］缪道平.城市轨道交通车体运用计划自动编制及优化研究［D］.北京:北京交通大学，2009.

［5］徐瑞华，陈菁菁，杜世敏.城轨交通多种列车交路模式下的通过能力和车底运用研究［J］.铁道学报，2005，27(4):6-10.

［6］吴涛.城市轨道交通共线运行图车底运用研究［J］.铁道运输与经济，2011，33(9):83-85，90.

［7］陶志祥.区域城际铁路与城市轨道交通跨线运行的兼容性分析［J］.城市轨道交通研究，2008，11(1):6-10.

［8］李代坤，何世伟，申永生，等.基于免疫克隆算法的综合交通枢纽布局优化研究［J］.武汉理工大学学报，2012，36(2):382-386.