“计算系数法”在混凝土结构设计中的应用

孙修礼

(青岛农业大学，山东 青岛 266109)

一、前言

建筑结构中的三大基本构件是梁、柱、板，其中梁和板主要受弯矩、剪力作用;柱主要承受压力作用，因此在弯、剪、压受力状态下构件的配筋问题是混凝土基本构件设计的重点［3］。构件的截面计算分为正截面承载力计算和斜截面承载力计算，在弯、压受力状态下进行正截面承载力计算，在剪切受力状态下进行斜截面承载力计算。正截面承载力计算是该混凝土结构设计的重点内容，楼板、单筋矩形截面梁、双筋矩形截面梁、T形截面梁、大偏心受压构件的设计都需要进行正截面承载力计算，其计算方法有“公式法”和“计算系数法”，“公式法”因为需要求解一元二次方程，计算工作量大且容易出错，而“计算系数法”因为简洁实用得到更多的使用［1］。

“计算系数法”是混凝土受弯构件设计计算的一种优化方法，它是在设计计算中通过设定系数αs、ξ，设定的系数αs、ξ可以根据已知条件直接求得，从而无需解一元二次方程而进行截面设计［2］。本文讨论“计算系数法”在钢筋混凝土基本构件设计中的统一应用，方便以后学习、设计需要。

二、计算系数法

以下简单介绍计算系数法:对于bxh的单筋适筋矩形截面，处于极限状态时，根据力平衡和力矩平衡可以建立两个独立方程:

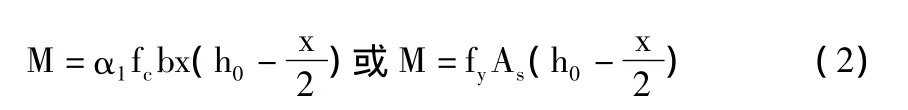
式中:fc—混凝土轴心抗压强度设计值;α1—系数，等效矩形应力图中混凝土压应力与fc的比值;b—梁截面宽度;x—混凝土受压区高度;fy—钢筋抗拉强度设计值;As—受拉钢筋截面面积;M—弯矩设计值;h0—截面有效高度。

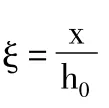
由式(3)和式(4)，只要求出 αs、ξ，就可以求出式(1)和式(2)中的x、As，即无需解一元二次方程，大大提高了计算速度。

三、“计算系数法”在结构设计中的应用

“计算系数法”可以将单筋矩形截面、双筋矩形截面、T形截面、大偏心受压构件有机地结合起来，从而无需求解一元二次方程，简单实用。

(一)单筋矩形截面

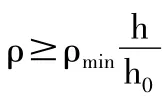
(二)双筋矩形截面

对于双筋矩形截面，其力平衡和力矩平衡方程为

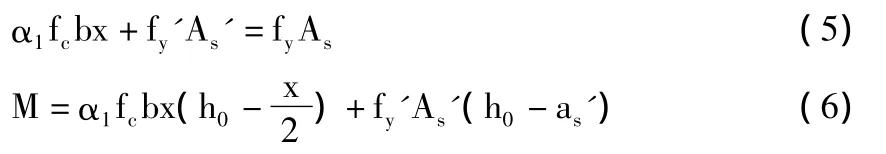
式中:fy'—受压钢筋受压强度设计值;As'—受压钢筋截面面积;αs'—受压区纵向受压钢筋合力点至截面受压边缘的距离;其它符号意义同前。

1.As、As'均未知

式中x、As、As'是未知数，两个独立的方程，三个未知数，因此需要补充条件以减少一个未知数，因为在双筋矩形截面梁中，受压钢筋和混凝土共同抵抗弯矩，所以让混凝土的抵抗能力发挥到极致可以节省钢筋，为保证受拉钢筋能够屈服，混凝土受压区高度x至多可以达到ξbh0，因此补充条件x=ξbh0，可求出式(6)中As'，进而可以求出式(5)中的 As。

2.As'已知

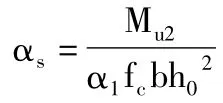
双筋梁应该满足的适应条件:(1)ξ≤ξb保证梁不是超筋梁即受拉钢筋能够屈服;(2)x≥2as'以保证受压钢筋屈服。至于最小配筋率一般不需验算。

(三)T形截面

1.第一类T形截面

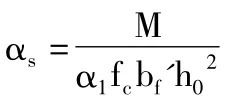
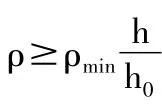
2.第二类T形截面

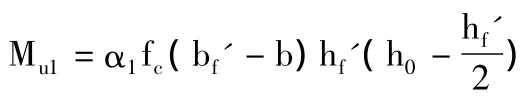
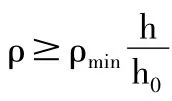
(四)非对称配筋大偏心受压构件

对于非对称配筋大偏心受压构件，其力平衡和力矩平衡方程为:

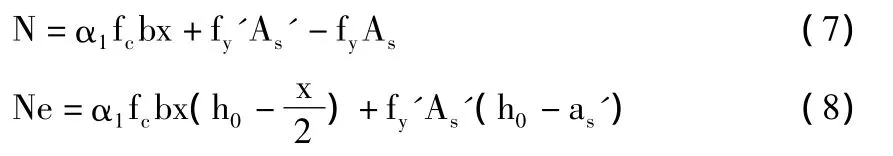
式中:N—轴向压力设计值;e—轴向压力作用点至纵向受拉钢筋合力点的距离;其它符号意义同前。

1.As、As'均未知

三个未知数，两个方程，参考双筋矩形截面中的情形1，从节约钢筋的角度补充x=ξbh0，这样就能保证式(7)和式(8)的求解。

2.As'已知

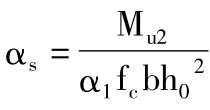
应该满足的适应条件:(1)ξ≤ξb保证受拉钢筋能够屈服;(2)x≥2as'以保证受压钢筋屈服。

四、结语

“计算系数法”无需解一元二次方程，方便实用。“计算系数法”可以方便地应用于受弯构件和偏心受压构件正截面承载力的计算:

(一)计算系数法可以用于单筋矩形截面的计算，避免求解一元二次方程;

(二)双筋截面在As'已知的情况下，求得受压钢筋能够承担的弯矩Mu1，总设计弯矩M减掉Mu1即为混凝土承担的弯矩Mu2，由Mu2可以利用“计算系数法”方便进行截面设计;

(三)对于第二类T形截面，与双筋截面梁类似，将翼缘挑出腹板范围的混凝土效应等同于受压钢筋，可以利用“计算系数法”方便进行截面设计;

(四)与双筋截面梁类似，非对称配筋偏压构件在As'已知的情况下也可以利用“计算系数法”方便进行截面设计。

［1］刘华新，魏巍.混凝土结构教学方法的研究与实践［J］.辽宁工学院学报，2001(9):90 －91.

［2］谢成新.混凝土结构设计原理［M］.北京:中国建材工业出版社，2012:52－54.

［3］王秋萍，李宏伟.混凝土结构课程的教学方法初探［J］.高等建筑教育，2005，14(1):59 －61.