大功率往复式压缩机活塞杆有限元分析

侯小兵 （江钻股份武汉压缩机分公司，湖北 武汉430040）

活塞杆是往复式天然气压缩机中关键的零部件之一，活塞杆一端与十字头相连，另一端与活塞相连，其作用是将驱动机输出的动力转换为气体的压缩力。在压缩机活塞由轴端向盖端运动过程时，活塞杆受压应力作用，当活塞由盖端向轴端运动时，活塞杆受拉应力作用，活塞杆就在拉应力与压应力交替作用下工作。

笔者以某型号大功率往复式天然气压缩机活塞杆部件为例，在Inventor中进行实体建模，使用分析软件ABAQUS对活塞杆模型进行了静力学分析，找出危险点位置，验证活塞杆在设计工况下的可靠性，并对活塞杆进行了前12阶自由模态分析，得出活塞杆的固有频率和振型，为活塞杆的设计及改进提供参考依据。

图1 定义“tie”约束

1 活塞杆－活塞组件有限元模型的建立与静强度分析

1.1 假设条件

根据活塞杆的结构形状特点，在活塞杆建模时，简化活塞杆两端和活塞螺母的螺纹结构，采用隐式通用接触算法 （General contact），接触属性为法向“硬”接触，切向摩擦系数为0。在活塞杆与活塞螺母螺纹连接处定义“tie”约束，如图1所示。

在活塞杆端面定义耦合关系，固定约束活塞端面，载荷施加于参考点RP上，如图2所示。

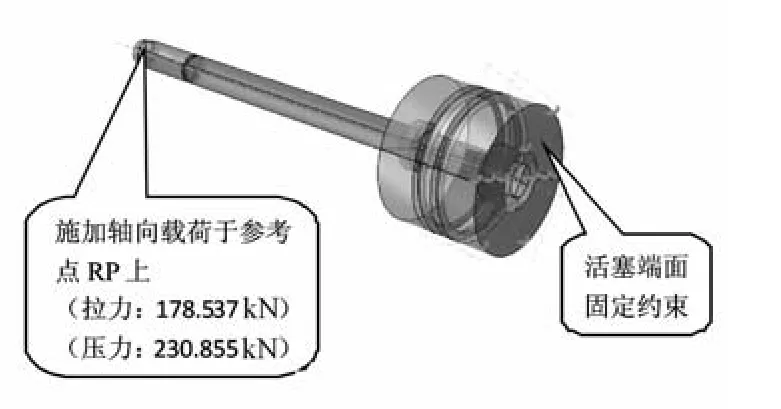
图2 载荷与边界条件

1.2 网格划分

在Inventor中建立实体模型并转换成.stp文件后导入有限元分析软件中计算。为了提高计算精度，网格模型采用一阶六面体单元C3D8R，单元数量为97597，如图3所示。

图3 网格划分

1.3 力学模型的建立

活塞杆在运动过程中需要承受气体压力、往复惯性力以及活塞所受的摩擦力，摩擦力采用下式计算［1］：

式中，Ff为往复摩擦力；Ni为级指示功；m为级膨胀指数；η为机械效率；S为活塞行程；n为级压缩指数。

往复式压缩机运动机构简图如图4所示，活塞杆－活塞组件在曲柄连杆机构的驱动下做往复直线运动。

笔者选取的分析对象为6列一级压缩对称式压缩机活塞杆，机组布置方式如图5所示。

压缩机对应的工况参数为：吸气压力2.8MPa；排气压力9.5MPa；一级压缩缸为双作用9in压缩缸。将上述工况代入计算软件后计算求得综合活塞力曲线。

图6所示为活塞杆综合活塞力曲线。由图6可知，当曲轴转角为113°时，活塞杆受最大拉伸力178536N；当曲轴转角为306°时，活塞杆受最大压缩力230855N。

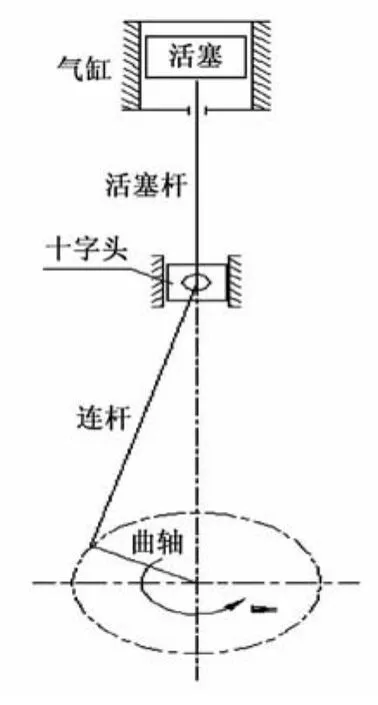
图4 压缩机运动机构简图

图5 机组布置图

1.4 活塞杆强度校核

根据1.3节中对活塞杆所受最大拉力178536N，最大压力230855N的工况，取活塞杆所受最大拉压力作为计算的边界条件来对活塞杆进行强度校核。

图7、图8为活塞杆在最大拉伸力与压缩力下的应力分布图。由图7、图8可知，当活塞杆受拉时，应力集中主要出现在十字头连接螺纹退刀槽和活塞杆台阶面与弹性段过渡圆弧处，最大Mises应力为63.6MPa，出现在十字头连接螺纹退刀槽处。当活塞杆受压时，应力集中主要出现在十字头连接螺纹退刀槽和活塞杆台阶面与弹性段过渡圆弧处，最大Mises应力为108.7MPa，出现在活塞杆台阶面与弹性段过渡圆弧处。

根据活塞杆强度分析结果，活塞杆在1.3节中所述的运行工况下，强度满足设计要求。同时，可以通过提高过渡圆弧的光洁度来减小十字头连接螺纹退刀槽应力集中，增加活塞杆台阶面与弹性段过渡圆角来减小变截面处应力集中，以达到提高活塞杆强度的效果。

图6 活塞杆综合活塞力图

2 活塞杆－活塞组件模态分析

模态分析用于确定设计结构或机器部件的振动特性 （固有频率和振型），固有频率和振型是承受动态载荷结构设计中的重要参数。采用兰佐斯向量迭代法 （Lanczos technique）进行活塞杆－活塞组件的模态分析。

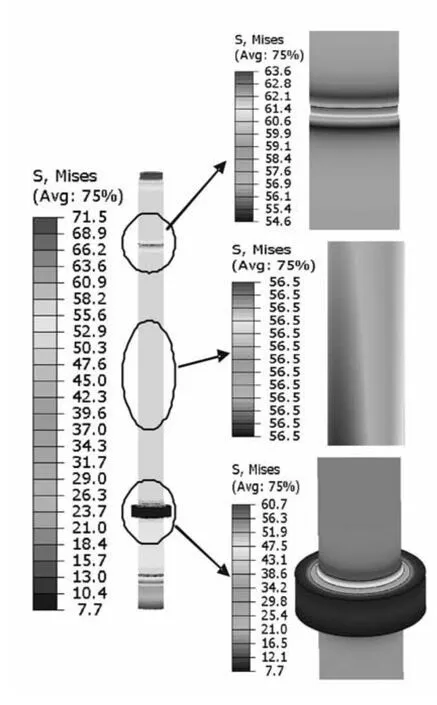
图7 活塞杆Mises拉应力分布

图8 活塞杆Mises压应力分布

模态是由系统的固有特性决定的，与外载荷无关，故不需要设置载荷边界条件。结构阻尼对固有频率的影响很小，在求固有频率和振型时，可以不考虑阻尼，则无阻尼自由振动方程：

式中，W 为自由振动固有频率；［M］为总体质量矩阵；［K］为总体刚度矩阵；｛q｝为结构的位移向量。

特征方程为：

展开行列式，得到一个关于W2的n次多项式的特征值，即为离散模型的固有频率，将特征值代入式（1），就可得出特征向量，从而获得给定频率下的振型［2］。

为了研究活塞杆在工作时是否会发生共振的问题，需要计算活塞杆的固有频率。为模拟该自由状态，在有限元分析时不附加任何约束力来计算活塞杆的自由模态。三维结构在无约束边界条件下的模态分析计算出来的前6阶模态接近于0，是所谓的刚体模态。因此真正有意义的模态应该是从第七阶模态开始。利用Block Lanczos法对活塞杆－活塞组件进行前12阶模态分析，在求解过程中，从1阶到6阶是活塞杆－活塞组件在坐标系中沿X，Y，Z方向上的刚体位移和在XY，YZ，XZ方向上的扭转位移，均在0Hz左右，所以主要分析7到12阶的计算结果。表1给出了活塞杆－活塞组件前12阶固有频率。

表1 活塞杆－活塞组件固有频率

由上面的计算结果和活塞杆－活塞组件模态振型可知。在活塞杆－活塞组件的后6阶振型中，其最低的频率为152.7Hz，随着阶次上升，其频率也相应增大，振型从弯曲逐渐过渡到扭转。从振型图上可以看出，活塞杆－活塞组件在低阶频率下，主要是以弯曲模态为主，最大振型位移出现在活塞杆尾端，在高阶次频率下，主要是以扭转模态为主。

图9 活塞杆－活塞组件7～12阶的振型图

激振频率的计算公式［3］：

式中，m为压缩机的级在曲轴一转的时间内从管道吸气或向管道排气的次数；n为压缩机额定转速，r／min。

该型号压缩机的工作转速范围600～1000r／min，根据式 （2）计算得出的激振频率范围20～33.3Hz。由模态计算结果可知，压缩机工作转速对应的频率小于第7阶的固有频率f＝152.7Hz（最小频率），因此该活塞杆－活塞组件发生共振可能性较小。

3 结 论

（1）通过对活塞杆受力分析表明，应力集中主要出现在活塞杆十字头连接螺纹退刀槽处和活塞杆台阶面与弹性段过渡圆弧处。最大压缩Mises应力63.6MPa，出现在十字头连接螺纹退刀槽处，最大拉伸Mises应力为108.7MPa，出现在活塞杆台阶面与弹性段过渡圆弧处，最大拉压应力均小于活塞杆材料许用应力。对于活塞杆强度薄弱区域，可以通过提高过渡圆弧的光洁度，增加连接处的过渡圆弧来达到减小变截面处应力集中、提高活塞杆强度的目的。

（2）由模态计算结果可知，活塞杆－活塞组件工作时对应的激振频率均小于第7阶的固有频率，因此活塞杆－活塞组件工作中发生共振的可能性较小。

（3）在活塞杆－活塞组件的振动过程中，弯曲、扭曲是该组件的主要变形形式，随着频率的增高，弯曲和扭转叠加所引起的危险振型便有可能发生，在一定的频率范围内甚至会变成波形扭曲。

（4）活塞杆－活塞组件在低阶频率下，主要是以弯曲模态为主，最大振型位移出现在活塞杆尾端，在高阶次频率下，主要是以扭转模态为主。

［1］王西来，陈燎原，凌志军 .基于Excel的往复空气压缩机动力计算 ［J］.压缩机技术，2008（1）：43－45.

［2］范校尉，樊文欣 .基于ANSYS的R6 1 05柴油机曲轴的模态分析 ［J］.机械设计与制造，2010（11）：37－38.

［3］西安交通大学压缩机教研室.活塞式压缩机设计 ［M］.西安：西安交通大学出版社，1979.