改进的RL正则化图像复原算法研究

赵 敏，陈 忠 （长江大学一年级教学工作部，湖北 荆州434025）

模糊图像复原就是根据观察到的退化图像重建理论上清晰图像的过程，是模式识别、图像理解与分析、计算机视觉的基础，并被广泛地应用于医学检测、军事探测、交通监控和天文研究等重要领域。目前最重要且最困难的问题是无参数 （Non－Parameter）模糊图像的盲复原，即此时的模糊核对应于成像设备的运动轨迹，而不再是用一个函数便可简单描述的直线运动情形。

对于模糊图像的盲复原，现在主要采取2种复原思路：①模糊核的估计和清晰图像的复原同时进行［1－2］；②先估计出模糊核，然后在已知模糊核的前提下进行图像复原。第2种思路较第1种思路降低了问题求解的不适定性，便于稳定和高效地复原模糊图像。Fergus等［3］结合自然图像的统计特征，在构建MAP（Maximum a Posterior）方程的基础上，利用集学习 （Ensemble Learning）理论很好地估计了运动模糊核。由于该MAP过程涉及大量的变量，使得模糊核的估计速度非常缓慢。在图像复原阶段，基于最大似然函数的Richardson－Lucy（RL）算法因其高效和稳定性得到广泛的研究和应用［4－6］。针对RL算法缺乏对解强加平滑性约束的不足，Tai等［7］基于双边正则化 （Bilateral）理论构建了改进的RL算法。鉴于该算法的复原结果依然存在振铃效应的问题，刘文等［8］在分析图像纹理信息几何特征的基础上，基于非局部正则化 （Non－Local）理论提出了改进的RL算法，显著提高了图像复原的质量，但因过高的计算复杂度限制了其进一步的应用。为此，笔者采用先估计模糊核后复原模糊图像的思路，借鉴Krishnan等［9］构建了一种改进的Richardson－Lucy正则化算法。

1 运动模糊核的估计

笔者所考虑的运动模糊情形为空间一致 （Uniform）的，即图像中各点被模糊的程度均相同，此时模糊图像的数学模型可以利用卷积的形式来表达：

式中，g为观察到的模糊图像；u为清晰图像；k为模糊核（或可称为点扩展函数PSF）；“⊗”表示卷积运算符；ε为服从独立同分布的零均值高斯白噪声。

对于运动模糊图像的盲复原，笔者先估计模糊核，然后在估计模糊核的基础上构建复原模型。在贝叶斯框架下，使用模糊核的拟合分布函数、噪声分布估计函数和自然图像的梯度估计分布函数等先验知识建立MAP方程来估计模糊核，虽然能够很好地得到模糊核的估计值［3，10］，但由于其过大的计算复杂度限制了其应用范围。

为提高模糊核的估计精度，笔者在图像的梯度空间构建相关的正则化模型。令x与y方向的梯度算子分别为 ▽x＝［1，－1］和▽y＝［1，－1］－1，对应的变量分别为x＝［▽xu，▽yu］1和y＝［▽xg，▽yg］1，并假设此时的加性高斯白噪声为ω，则像素空间中的数学模型（1）在梯度空间中转换成：

按照文献［9］估计运动模糊核的思路，得到相对应的正则化模型：

因求解模型（3）是一个典型的非凸优化问题，此时将其转化成2个子问题的求解，即：

并分别利用收缩阈值迭代算法和加权迭代最小二乘算法求解子问题，即可稳定有效地得到运动模糊核，接下来的工作便在估计模糊核的基础上构建图像复原模型。

2 改进的Richardson－Lucy正则化方法

模糊图像的复原可看作是模糊成像 （1）的逆过程，即由观测的模糊图像g、模糊核k和图像先验信息估计清晰图像u的过程。模糊图像的复原是一个典型的不适定性问题，因模糊核的测量误差或观察图像存在的污染噪声都会对最终的复原结果产生较大的影响。在估计运动模糊核的基础上，笔者在贝叶斯框架下来对模糊图像进行复原，此时模糊图像复原的过程可表示为［8］：

由条件概率公式可知：

联立式（6）与式（7）得到：

式（8）即为改进的Richardson－Lucy正则化算法（MRL）。下面重点研究P（g，k｜u）和P（u）。为抑制复原图像中的振铃效应，充分利用图像像素空间和梯度空间的统计性质，令P（g，k｜u）＝Pu（g，k｜u）P▽u（▽g，k｜▽u），此时式（8）转换成：

因ε和ω均为服从独立同分布的零均值高斯白噪声，假设其标准差分别为σε和σω，则依据噪声的分布特征有：

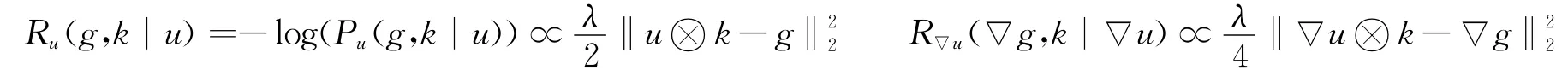
接下来考虑对自然图像的梯度约束R（u）。该问题在本质上反映了对自然图像梯度概率分布函数的拟合，笔者采用较为简洁的Hyper－Laplacian函数作为先验信息P（u）的逼近，即对应的R（u）＝｜▽u｜p。依Krishnan对自然图像Hyper－Laplacian分布的研究，广义系数p取0.8较为合适［11］，则模糊图像复原对应的能量泛函为：

利用梯度下降法，可得到能量泛函（10）对应的迭代求解公式，即改进的Richardson－Lucy正则化算法：

式中，λ，γ＞0均为正则化参数。式（11）后2项为正则化项，用来克服原有RL算法易产生振铃现象的缺点。为增强MRL在复原模糊图像中的反扩散能力，以锐化复原图像的边缘与轮廓，笔者在局部坐标系下对式（11）的最后1项进行离散，即：

利用傅里叶变换及其逆变换得到正则化项Φ（·）的表达式为：

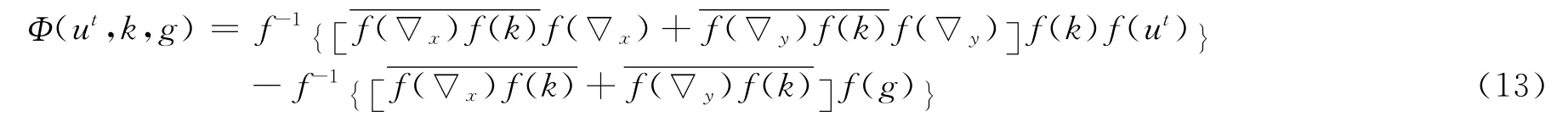
式中，f和f－1分别表示傅里叶变换和傅里叶逆变换，且为f（·）的复共轭矩阵，设迭代初始值为u0＝g。

3 试验结果及分析

为验证MRL算法在模糊图像复原中的有效性，现以未知模糊核的Girl图像为例进行试验，并与Fergus［3］和 Krishnan［9］的图像复原结果 （见图1）进行比较分析。试验在 CPU Intel（R）2.0GHz、1G内存、Matlab 7.0的环境下进行。正则化参数分别为λ＝1和γ＝0.5，且该迭代算法满足如下的停机准则：

由图1可以看出，Fergus的复原结果不能很好地再现目标图像的纹理细节结构，且存在一定的振铃效应；Krishnan方法虽在一定程度上能克服振铃效应的产生，但由于所选取的超拉普拉斯先验信息不能很好地拟合自然图像的梯度分布，使得复原图像存在过平滑的问题，这在局部放大图像中可清晰地观察到这一不足；笔者提出的改进的RL正则化算法对图像复原的结果施加更强的约束性，即使模糊核估计存在一定的误差，该算法依然能够有效地复原模糊图像，再现图像中的纹理细节信息，并能有效地抑制复原图像中产生振铃效应。

图1 模糊图像Girl的复原结果比较

［1］Chan T F，Wong C K.Total variation blind deconvolution ［J］.IEEE Transactions on Image Processing，1998，7 （3）：370－375.

［2］Shan Q，Jia J Y，Agarwala A.High－quality motion deblurring from a single image ［J］ .ACM Transactions on Graphics，2008，27 （3）：73：1－10.

［3］Fergus R，Singh B ，Hertzmann A，et al.Removing camera shake from a single photograph ［J］ .ACM Transactions on Graphics，2006，25 （3）：787－794.

［4］Richardson W H.Bayesian－based iterative method of image restoration ［J］.Journal of the Optical Society of America，1972，62 （1）：55－59.

［5］Lucy L.An iterative technique for the rectification of observed distributions ［J］ .Astronomy Journal，1974，79 （6）：745－753.

［6］闫河，闫卫军，李唯唯 .基于Lucy－Richardson算法的图像复原 ［J］.计算机工程，2010，36（15）：204－205.

［7］Tai Y W，Tan P，Brown M S.Richardson－Lucy deblurring for scenes under a projective motion path ［J］ .IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33 （8）：1603－1618.

［8］刘文，吴传生，吕琪 .含噪径向模糊图像的复原算法研究 ［J］.武汉理工大学学报，2011，33（4）：139－143.

［9］Krishnan D，Tay T，Fergus R.Blind deconvolution using a normalized sparsity measure ［C］.IEEE Conference on Computer Vision and Pattern Recognition.Colorado Springs：IEEE Computer Society，2011：233－240.

［10］Levin A，Weiss Y，Durand F，et al.Understanding and evaluating blind deconvolution algorithms ［C］ .IEEE Conference on Computer Vision and Pattern Recognition.Miami：IEEE Computer Society，2009：1964－1971.

［11］Krishnan D，Fergus R.Fast image deconvolution using Hyper－Laplacian priors ［C］ .Advances in Neural Information Processing Systems.Vancouver：MIT Press，2009：1－9.

［12］Aubert G，Kornprobst P.Mathematical problems in image processing：partial differential equations and the calculus of variations ［M］ .New York：Springer，2006.