原型-集合理论在二语代词和连词分析中的应用

刘振标 崔艳嫣

(聊城大学,聊城,252059)

1. 研究背景

自创立以来,原型理论在很多方面都得到了蓬勃发展,广泛应于各个领域及学科(如文学、语言学等),衍生了许多相关理论(如家族相似论等)。近年来,原型理论及其相关衍生理论的发展已经涉及到语言学研究的众多方面,在文献中开始出现对其所进行的大量论述和许多具体的应用。由于集合理论中集合之间的各种关系,集合与子集之间、子集与子集之间的各种关系,以及原型范畴理论中各范畴之间的关系再加上范畴与子范畴,及子范畴之间的各种关系,具有惊人的相似性,本研究认为可以用集合理论构建各种范畴的原型,并对这些范畴的原型进行解释和说明,从而使原型理论在语言学习,尤其是在第二语言的词汇学习研究中得以更好地应用。更具体地说,本研究旨在通过对原型集合理论在二语代词和连词分析中具体应用的论述,来证明这一理论在这一研究领域应用的有效性,认为这为二语词汇习得提供一个新的角度和途径,将对二语词汇习得研究产生重大意义。

2. 原型理论、集合论研究综述

2.1 原型范畴理论发展回顾

早在2000多年前亚里士多德就对范畴有过非常经典的论述,德国哲学家康德(Emmanuel Kant)也对范畴进行了研究,并建立了范畴框架。原型理论的鼻祖则是英国人类学家爱德华·泰勒(Edward Burnett Tylor),而在荣格这里原型理论得到了更大的发展,他在早年就已经提出了集体无意识的学说,后来则成为荣格分析心理学的核心内容,荣格最终找到了把象征形式与集体无意识的存在统一起来的实体,并且将这种实体命名为“原始意象”,之后又更名为“原型”。由于Wittgenstein(2003)的家族相似性的理论的提出,使得原型范畴理论的发展又向前迈进了一大步。根据Zadeh(1965)的模糊集合论(Fuzzy Set Theory),将“Fuzzy Sets”定义为“带有资格等级连续集的对象的一个类”,并规定“这样一个集合由资格(特征)函数表征,资格函数赋予每个对象一个取值于0到1区间之内的资格等级。”他的模糊集合理论为语义学研究提供了一种分析范畴语义模糊性的有效方法,他用模糊集来描述人类语言和思维中及客观世界中存在的模糊现象,即范畴中的成员向非成员过渡中的一种连续的、递进的隶属关系,使得我们对于范畴内部结构的深化研究有了新的角度和方法。

当前原型范畴理论及其发展,以及它在各个领域中的应用日新月异,在各国学者的努力下,可谓是硕果累累。刘振标等(2013)根据web of science数据库中搜集到的相关数据,对其研究发展进行了分析,发现自20世纪90年代以后,原型理论及其相关衍生理论(如家族相似论)在全世界范围内飞速发展,尤其是在美国的发展,非常突出,相对于其它各国来说,占有绝对优势的地位。原型理论在中国的发展虽然也居世界前几位,但相对于美国来说,还有很大的差距,家族相似性理论的研究探索和美国相比差距则更大,很多领域和方面还没有涉及到或所涉不深,有很多方面的问题亟待研究者们去研究和解决。

2.2 集合论、原型-集合理论与二语词汇习得

集合论(Set Theory)是数学界最富创造性的伟大成果之一,是由德国数学家康托尔在19世纪末创立起来的。集合论从集合的直观概念出发研究集合上的运算、顺序,特别是各种超穷数的性质,并用集合定义各种数学对象,包含了集合、元素和成员关系等基本数学概念,集合论为现代数学的大多数公式提供了如何描述数学物件的语言。康托尔在建立集合论时没有使用公理化和形式化的方法,集合是被用作为一堆物件构成的整体之类的自证概念,后来就将这种没有使用公理化和形式化方法的集合论称为朴素集合论。集合论的进一步发展是公理化集合论,它除了用公理化和形式化的方法处理朴素集合论的内容之外,更重要的是研究集合论形式公理系统的元数学性质——集合论的模型、各公理之间的关系、各系统之间的关系、各种不可判定语句,以及集合论研究过程中所提出的种种新方法和新问题。在公理化集合论中,集合和集合成员并不是直接被定义,而是先规范可以描述其性质的一些公理,按现代数学观点,数学各分支的研究对象或者本身是带有某种特定结构的集合如群(group)、环(ring)、拓扑空间(topological space),或者是可以通过集合来定义的如自然数、实数、函数等。从某种意义上说,集合论可以说是整个现代数学的基础。

语言学研究领域,特别是在语义学和词汇学以及第二语言词汇习得方面,在众多的研究成果中,多数研究者只注意了模糊集合的模糊性,却没有学者用集合的方法,建立起数学模型,即集合原型,用数学和逻辑推理的方法,对词汇进行分析和研究(即本文后面所述的原型-集合理论),并运用于第二语言词汇习得,以此来推动第二语言习得,特别是词汇习得的发展。有些学者已对原型理论在词汇习得的各个方面进行了研究。如在袁毓林(1995)中,把词共分为17类,并且进行了相应说明。再如Year和Gordon(2009)运用原型理论对双宾结构中的动词进行了分析,文中通过建立高频双宾动词原型,分别对韩国儿童习得英语中六类高频双宾动词的习得机制进行了研究。也有人对介词进行了分析,如Kodachi(2005)运用原型理论对介词的习得进行了研究,他通过不同母语习得者(母语为日语和菲律宾语)对英语中介词at、in、on的原型的不同理解,及该介词在母语中的理解和其对该介词英文原型的理解的不同,进行了对比研究。但上述研究仍然存在多方面不足。如袁毓林的研究只是把某一词类共同作为一个范畴(或可称之为一个家族)来进行分析,而并没有对具体词类的具体词或该类词的个例进行分析,因而对二语词汇习得中具体词的习得方面并无多大作用;而Year等以及Kodachi的研究都没有构建起具体词的原型,以能对词汇习得方面使习得者对具体词有原型的概念,以此对二语词汇习得有积极作用,其大多数都是对词类或某一词类泛泛而谈,目前还没有学者很有针对性地对某一词类进行细化说明,特别是运用集合理论进行说明。

笔者经过研究,认为通过建立数学集合模型,来建立各种词汇的原型,并且运用数学和逻辑推理的方法对各种词类中的具体词进行分析,即原型-集合理论是可行的。

3. 原型-集合理论及其在二语词汇分析中的应用

下面笔者就应用原型-集合理论对各词类具体词进行实际论证。在论证之前,首先我们要界定词的分类,本文采用传统的词类分类方法(李基安2000),如名词、动词、形容词、副词、介词、连词等。本文将以代词和连词为例,对原型-集合理论在二语词汇习得中的运用进行阐述。有关集合理论及其推理方法,我们将采用Enderton(2006)中的各种符号表示及相关原理和论证方法。具体论证实例如下。

3.1 代词

代词可分为人称代词、物主代词、表量代词、地点代词及反身代词等。

(1) 人称代词

人称代词可分为第一人称、第二人称和第三人称代词,每一种人称代词又可分为单数和复数,且每一种人称代词的单数和复数形式又可进一步分为主格和宾格。在这一分类上,英国著名语言学家Radford(2004)则采用的是另一说法,他把人称代词总体上分为主格形式(nominative case form)、宾格形式(accusative case form)和属格形式(genitive case form)即我们后面所要论证的物主代词,这一点和我们的传统说法略有差别。我们用集合理论可对人称代词进行以下说明:

题设。设定集合A为第一人称代词,B为第二人称代词,C为第三人称代词,其中A、B、C中的元素均用变量t表示,A可表示为A={t|t=I,we,me,us},B={t|t=you1,you2,you3,you4},C={t|t=he,she,it1,they,him,her,it2,them};设定集合D为主格代词,E为宾格代词,其中D,E中的元素用变量t表示,D可表示为D={t|t=I,we,you1,you2,he,she,it1,they},E可表示为E={t|t=me,us,you3,you4,him,her,it2,them};设定集合F为单数人称代词,G为复数人称代词,其中F,G中的元素用变量t表示,F可表示为F={t|t=I,me,you1,you3,he,him,she,her,it1,it2},G={t|t=we,us,you2,you4,they,them,这样,我们就建立起了有关人称代词的各种原型-集合。

证明。如我们要表示第一人称单数宾格,就可以用t表示为t=A∩E∩F={t|t=I,we,me,us}∩{t|t=me,us,you3,you4,him,her,it2,them}∩{t|t=I,me,you1,you3,he,him,she,her,it1,it2}=me,再如我们要表示第三人称主格表物单数代词,则可表示为t=C∩D∩F={t|t=he,she,it1,they,him,her,it2,them}∩{t|t=I,we,you1,you2,he,she,it1,they}∩{t|t=I,me,you1,you3,he,him,she,her,it1,it2}=it1。同样道理如果我们要表示第三人称宾格复数代词,则可表示为t=C∩E∩G={t|t=he,she,it1,they,him,her,it2,them}∩{t|t=me,us,you3,you4,him,her,it2,them}∩{t|t=we,us,you2,you4,they,them}=them。由此,人称代词的其它各种形式均可同理得到解释说明。

以上的论述用原型-集合的图示法也可以得到直观的说明,如图1:

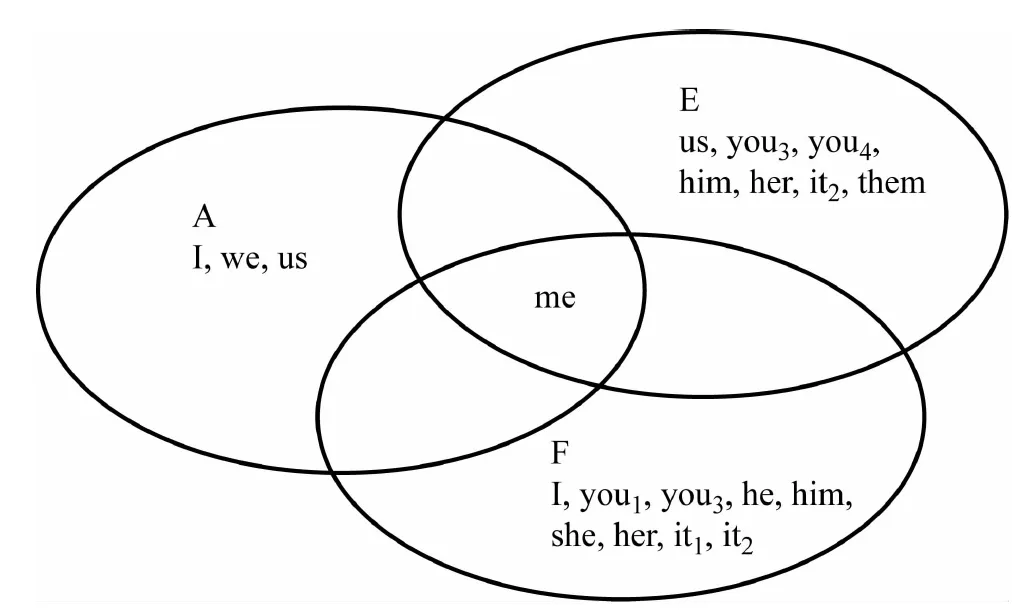
图1第一人称单数宾格原型-集合理论图示法①

即:t=A∩E∩F=me

(2) 物主代词

物主代词可以分为形容词性物主代词和名词性物主代词,在这一问题上,Radford(2004)采用了另外一种说法,即弱式(weak form)和强式(strong form),我们传统上称为形容词性物主代词,Radford则称为weak form,而我们传统上称为名词性物主代词,Andrew Radford则称为strong form,这两种方式虽然叫法不同,但内容实质上是一样的。下面我们用原理-集合理论对其进行分析说明。

题设。设定集合A为形容词性物主代词,A中的变量用t来表示,则A可表示为A={t|t=my,our,your1,your2,his1,her,its1,their};集合B为名词性物主代词,B中的变量亦用t来表示,则B可表示为B={t|t=mine,ours,yours1,yours即:t=A∩E∩F=me2,his2,hers,its2,theirs};集合C为第一人称物主代词,t为集合C中表示元素的变量,则C可表示为C={t|t=my,our,mine,ours},D为第二人称物主代词,t为集合D中表示元素的变量,则D可表示为D={t|t=your1,your2,yours1,yours2},E为第三人称物主代词,t为集合E中表示元素的变量,则E可表示为E={t|t=his1,her,its1,their,his2,hers,its2,theirs};集合F为单数物主代词,集合F中的元素用变量t表示,则F可表示为F={t|t=my,mine,your1,yours1,his1,her,its1,his2,hers,its2},集合G为复数物主代词,集合G中的元素用变量t表示,则G可表示为G={t|t=our,ours,your2,yours2,their,theirs}。

证明。如果我们要表示出第一人称单数形容词性物主代词时,就可用t表示为t=A∩C∩F={t|t=my,our,your1,your2,his1,her,its1,their}∩{t|t=my,our,mine,ours}∩{t|t=my,mine,your1,yours1,his1,her,its1,his2,hers,its2}=my,其他各个物主代词也可同理得到阐述和证明。

和人称代词一样,物主代词的这种论证方法也能用原型-集合的图示法得到证明,如果要表示第一人称单数形容词性物主代词,如图2所示。

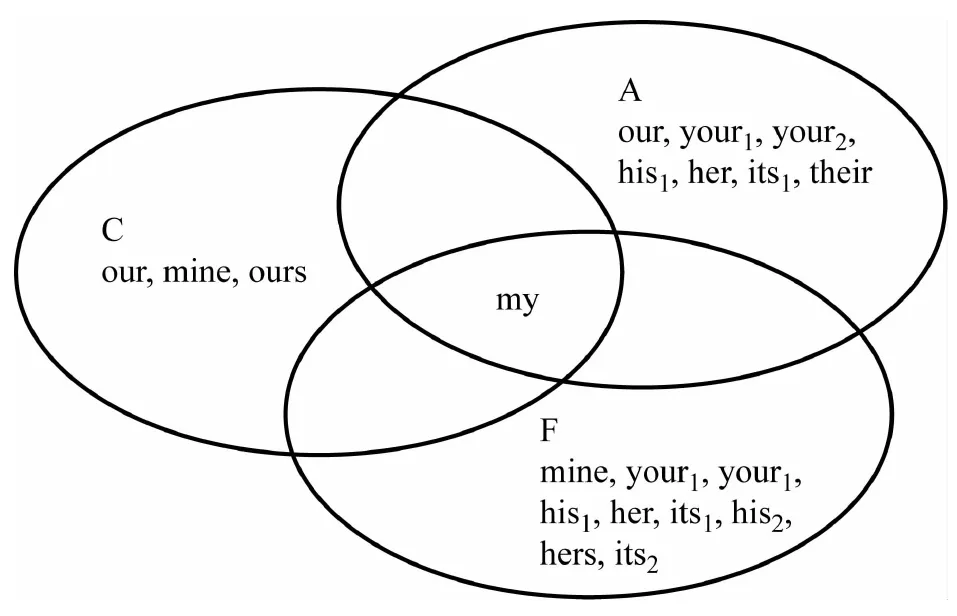
图2第一人称单数形容词性

物主代词原型-集合理论图示法②

即:t=A∩C∩F=my

(3) 反身代词

和人称代词,物主代词一样,我们同理可证明运用原型-集合理论对反身代词的分析也是可行的。而这种论证方法也能用原型-集合的图示法得到直观的说明③。

(4) 表量代词:some,all等。

题设。设定集合A,A中的元素用变量t表示,A中有十个元素,分别为a,b,c,d,e,f,g,h,i,j,表示为A={t|t=a,b,c,d,e,f,g,h,i,j}

证明。如果表示a,b,c...等是A的元素,我们可以表示为:a∈A,b∈A,c∈A...那么如何表示代词some和all呢,虽然在Semantics(Saeed,2000)第十章也有相关论述,但在那里说的不是对some和all的原型解释和说明,而是用逻辑推理的方法进行的阐述,如果使用原型理论我们可以进行以下说明:如果十个元素a,b,c,d,e,f,g,h,i,j都列出,即{a,b,c,d,e,f,g,h,i,j}和A的关系为{a,b,c,d,e,f,g,h,i,j}=A,则说明这些元素对A来说是“all” in A,如果只列出一个或一到九个中的任何几个,则只能说“some” in A.如果推广到A中含有更多个,或无数个元素也可以同理说明。

(5) 地点代词

地点代词如here,there...这类代词用集合原型的图示法就可直观地得到说明,如图3-4所示。

题设。设定集合A,且a,b,c...为集合A中的元素,设定集合B,且m,n,k...为集合B中的元素,另设参照物,且参照物和集合A,B的相对关系如图3所示:

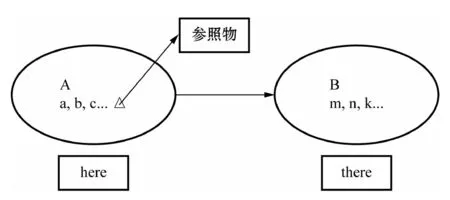
图3地点代词如here,

there原型-集合理论图示法

由图3所示,我们可以看出,对于集合A中的元素(如a,b,c...)和参照物的关系都可以表示为here,我们指代a,b,c...的位置关系时都可以用here来表示;而对于集合B中的元素(如m,n,k...)和参照物的关系都可以表示为there,因此我们指代m,n,k...的位置关系时都可以用there来表示。

3.2 连词:如but,and,while...

(1) but的原型-集合理论表示方法

题设:设定集合A,A中的元素用变量t表示,假设A中有十个元素,分别为a,b,c,d,e,f,g,h,i,j,表示为A={t|t=a,b,c,d,e,f,g,h,i,j}

证明。如果表示a和b都是A的元素,就可以表示为(a & b)∈A,这样and就得到了说明,对于连词but,可能用逻辑学推理方法进行说明比较容易,能不能用原型理论进行论述呢？答案是可以的,如果具体各个事件用a,b,cd,e,f,g,h,i,j来表示,A表示这些事件的集合,A中的元素用变量t来表示,则A可表示为A={t|t=a,b,c,d,e,f,g,h,i,j},另有一些事件k,l,m,n,o,p,它们的集合用B来表示,把B中的元素用变量t来表示,即B={t|t=k,l,m,n,o,p},如果表示事件n不属于A,但是属于B,就可以表示为but:(nA,n∈B),这样,but就得到了说明。

(2) while的原型-集合理论表示方法

当一些词同时有几个意义时,必须分别进行说明,比如说while,有两层意义,表示“同时”,和表示转折“然而”,以下是对其进行的具体说明:

a. 当while表示“同时”时。

我们把事件A(eventA)用集合A和把事件B(eventB)用集合B来表示,即在事件A发生的过程中,事件B也发生了或进行中,则事件A和事件B的关系用图示法能够很清楚地表示出来,可表述为:

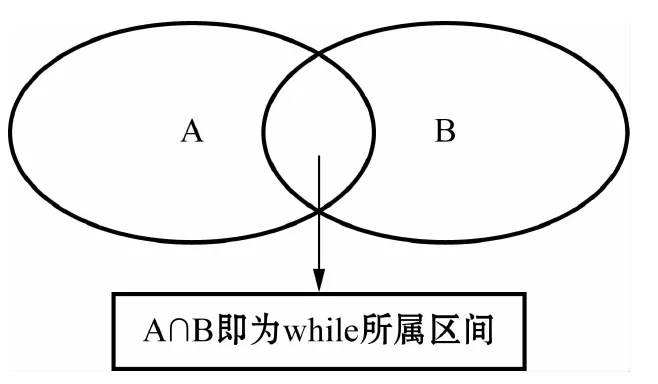
图4while表示“同时”时的

原型-集合理论图示法

如图4所示,这种表示方法能很好的说明while所反映出的A和B的关系:A开始发生的时间不一定和B一样,A结束的时间也不一定和B一样,同样,B也不一定和A同时发生和结束,但在事件A的过程中,有和事件B重合的部分,这个期间,即为while所表示的A和B发生关系的时间区间,用文字可表述为:

while: A∩B

b. 当while表示“然而”时。

如在TheMayorofCasterbridge(Thomas Hardy 1886)一书中:

Three glasses stood at his right hand; but, to his wife’s surprise, the two for wine were empty, while the third, a tumbler, was half full of water.

在这句话中,while显然不能理解为“同时”,而应该理解为“然而”,即the two for wine were empty和the third,a tumbler,was half full of water所述的很容易看出不是一回事,我们把事件(event) the two for wine were empty设为集合A,把事件(event) the third,a tumbler,was half full of water设为集合B,则A中所涉及的元素(element)如the two,wine, empty,和B中所涉及的元素(element)如the third,water,half full,是一种对比和转折的关系,即A中元素所陈述的事件的性质(qualityA)和B中元素所陈述的事件的性质(qualityB)是相反的或不一样的,因此,在这里while:QualityA≠QualityB,这样以来,while的意义运用原型-集合理论就得以明析的阐释。

以上是以代词和连词习得为例,运用原型-集合理论对第二语言词汇分析中各个具体词类的阐述,由此论述我们可以看出,原型-集合理论是我们进行二语词汇分析的有效手段,大大有助于我们第二语言词汇的学习与教学,并且非常有利于我们进行词汇习得方面的研究。当然,在具体分析过程中,我们可以综合运用各种方法,如图示法,描述法,逻辑推理等,使得我们的习得手段多样化,更有利于我们的第二语言习得研究的进展。

4. 讨论

通过上述证明,我们知道原型-集合理论可以应用于代词和连词分析,那么有关其他词类是否也可以用原型-集合理论进行阐述呢？这个问题有待于进一步探讨。如名词在所有词类中最为复杂,其分类多种多样,在现行的各种著作和论述中以及不同的学科领域和学派中,关于它也有着不同的分类标准,普通来说,分为抽象名词(如culture,knowledge等)和实体名词(自然界中存在实物的名词通常都可称为实体名词,如hill、car、house等),而对于抽象名词来说,又可分为抽象物名词(如God、Zeus、Venus等)和纯抽象词(如abstract、concept等)……运用原型-集合理论对名词进行解释说明时,必须针对各种不同的分类和各类名词的特点,分别采用不同的集合原型进行解释说明,因此对名词的说明是一件非常复杂的工作。但是原型理论在语言学中的对名词的解释说明,是不可缺少的一个方面,因此,对名词的阐释又是非常必要的。再如动词:在英语中,英语又可分为行为动词,系动词,助动词和情态动词等。而对于动词的解释和名词一样,也非常复杂且又特别重要。当然,我们不能不提到形容词,这部分词只有少部分能用原型-集合理论来解释,如full、empty等。而对于副词:和形容词类似,有些词可以用原型-集合理论进行很好地论述,如completely、firstly、secondly等,而有部分词则不容易解释说明,如she had thought of love just before she went in,and had innocently asked Aziz what marriage was like, and she supposed that her question had roused evil in him(Zhang 2005)中的innocently,运用原型-集合理论就不能很好地说明这个副词。其它词类如助词、语气词、叹词、拟声词,量词等也都是二语词汇习得中非常重要的方面,诸如此类,笔者将另撰文加以讨论。

5. 结论

在运用原型-集合理论进行论述时,对于代词及连词能非常有效地进行阐释说明,对于形容词及副词只有少数词比较容易得到解释说明,而其余的词如beautiful,nice等则很难用原型-集合理论进行说明。对于其它词类如助词、语气词、叹词、拟声词,量词等目前研究者甚少,有待于进一步探索和研究,而对于名词和动词的原型理论研究则是硕果累累,出现了不少研究方法和角度,虽然有人用模糊集合的理论进行研究,也出了不少成果,但那种方法却不能对范畴内部即具体的词语进行阐述说明,因此具有很大缺陷。目前还没见有学者运用原理-集合理论进行深入细化研究,因此原型集合理论应用于二语词汇分析将面临很多问题,亟待研究者们去研究和解决。

通过本研究对原型范畴理论和家族相似性理论的发展和以上对于原型-集合理论在二语词汇分析中的应用的论述来看,原型-集合理论能非常有效地应用于二语泀汇分析过程中,是我们进行二语习得研究的一个非常好的途径,对进行二语词汇学习和教学研究提供了一个非常好的方法和研究视角,能大大增进研究者对二语词汇习得方法的理解和提高二语词汇习得研究的效率。在外语教学实践中,如果教师能通过上述途径,建立各种代词和连词的集合,教授给学生,可以实现快速、直观、高效的教学,使学生对所学知识先有了一个集合化的原型的认识,这将使学生理解、接受速度得以快速提高,从而大大提高教学效率。同时,如果学习者在二语词汇习得过程中,运用上述方法,则能快速、准确地掌握所学内容,使学习效率迅速提高。因此,将原型集合理论应用于二语词汇习得是我们以后进行第二语言习得研究的一个重要方法,原型理论及其在各领域的应用有着非常重要的研究价值,很值得我们去探索,去研究。

附注

① 在实际书写过程中,you1,you2,you3,you4和it1,it2只需写成统一的you和it就行了,不必加以区分,这里是为了方便说明问题。

② 在实际书写过程中,your1,your2,yours1,yours2,his1,his2,its1,its2,只需写成your,yours,his和its就行了,这里只是为了说明问题的需要。

③ 由于篇幅所限,这里将此论证过程和图示略去。

Enderton, H. B. 2006.ElementsofSetTheory[M]. Beijing: Posts and Telecom Press.

Hardy, T. 1886.TheMayorofCasterbridge[M]. Oxford: Oxford World’s Classics.

Kodachi, K. 2005.AStudyofPrototypeFormationoftheMeaningsofPrepositionsbyJapaneseandFilipinoLearnersofEnglishfromthePerspectiveofCognitiveLinguistics[R]. Proceedings of the 10th Conference of Pan-Pacific Association of Applied Linguistics. 105-28.

Radford, A. 2004.EnglishSyntax:AnIntroduction[M]. Cambridge: Cambridge University Press.

Saeed, J. I. 2000.Semantics[M]. Beijing: Foreign Language Teaching and Research Press.

Wittgenstein, L. 2003.PhilosophicalInvestigations[M]. Oxford: Blackwell.

Year, J. & P. Gordon. 2009. Korean speakers’ acquisition of the English ditransitive construction: The role of verb prototype, input distribution, and frequency [J].TheModernLanguageJournal93(3): 399-417.

Zadeh, L. A. 1965. Fuzzy sets [J].InformationandControl(8): 338-53.

Zhang, B. 2005.ACourseBookofEnglishLiterature(VolumeTwo) [M]. Wu Han: Wu Han University Press.

李基安.2000.现代英语语法[M].北京:外语教学与研究出版社.

刘振标、刘佳、崔艳嫣.2013.原型理论及其相关理论发展的研究[J].信阳师范学院学报33(2):73-77

袁毓林.1995.词类范畴的家族相似性[J].中国社会科学(1):154-70.