基于克雷格插值的反例理解方法
2013-12-03黄宏涛黄少滨陈志远
黄宏涛, 黄少滨, 陈志远, 张 涛
(哈尔滨工程大学 计算机科学与技术学院, 哈尔滨 150001)
模型检测技术[1]的主要优势是它能在证明模型不满足给定规范的同时自动给出反例, 但模型检测器给出的反例仅反映了模型缺陷的症状, 验证者仍需花费大量时间和精力理解反例, 以确定产生模型缺陷的原因. 在实际应用中, 模型检测器给出的反例越来越长, 从反例中分析迹失效的原因已被证明为NP完全问题[2]. 因此, 寻找高效的算法进行反例自动理解已成为模型检测技术亟待解决的问题.
近年来, 如何从反例中发现模型缺陷的源头已引起研究人员的广泛关注. 文献[3-5]给出了自动提取失效原因以简化程序调试工作的方法. Beer等[6]提出的反例理解方法把反例中引起规范失效的部分定义为一组原因, 这些原因在因果关系模型[7]框架下被标记出作为可视化的解释呈现给用户, 该方法已应用于IBM形式化验证平台Rulebase PE, 并显著加速了反例理解的速度. 与基于最小不可满足核方法[8-9]相比, 基于因果关系的方法能给出理解反例所需的全部相关信息, 且这些信息是以单个失效原因集而不是一组原因集的形式给出. 此外, 这种基于因果关系反例理解方法的应用独立于各种模型检测器, 但这种与模型无关的方法也给从错误原因到具体错误代码的映射工作带来困难.
Jose等[10]把MAX-SAT求解机每次迭代过程中的不可满足子句作为潜在错误位置, 其增量式SAT求解该方法能显著降低迭代过程的时间开销. 由于MAX-SAT的判定是NP完全问题, 且该方法没有对迹进行缩减, 故其仅适合于对规模较小的反例进行理解. Wang等[11]使用基于路径的语法级最弱前置条件算法辅助反例理解, 该方法从反例中提取一个最小原子命题集作为反例不可行的证明, 这种语法级的证明能通过转换语句直接把反例理解结果映射到错误源码. 由于最弱前置条件的计算被约束在单个执行路径上, 且最弱前置条件本身计算代价较低, 因此这种反例理解方法具有更好的可扩展性. 然而, 其不可行最小证明的求解过程需要对公式中所有文字进行逐个测试, 每个测试过程都会触发一个计算代价较高的SAT求解过程. 为了提高错误原因的提取效率, 本文提出一种利用克雷格插值从初始状态与反例最弱前置条件的不一致证明中提取模型失效原因的方法, 该计算过程能在线性时间内完成.
1 基本定义
本文用文献[12]的方法定义程序: 令V={v1,v2,…,vn}为程序变量集;D1,D2,…,Dn分别为v1,v2,…,vn的数据域; Evt为程序中的事件集, 事件e∈Evt是定义在V上的一个条件指派:

(1)

定义1Kripke模型为一个四元组K=(S,→,I,L), 其中:S⊆D1×D2×…×Dn为状态集合,n=V; → ⊆S×Evt×S为迁移关系集合, (s1,e,s2)∈→当且仅当T(s1,e)=s2,e∈Evt,s1,s2∈S,T:S×Evt ⟹S为状态转换函数, 其作用是当s1满足e的守护条件时,e通过指派动作把s1转换为s2;I⊆S为初始状态集合;L:S⟹ 2AP为标记函数,AP为原子命题集合.
状态的交替反映了程序语句执行引起的变量变化, 所以模型检测的反例通常由状态序列构成. 因为由反例路径上的两个相邻状态可在线性时间内确定引起状态变迁的事件, 所以本文把路径定义为状态事件的交替序列. 与文献[6]仅从反例提供的状态序列中寻找错误原因不同, 本文的反例理解方法是与模型相关的, 因此该方法可以直接把反例理解结果映射到源码.
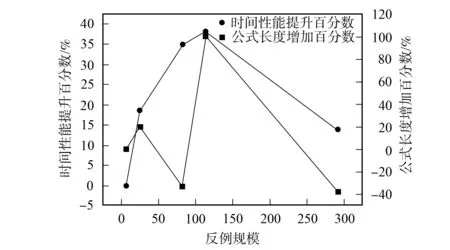
定义2令K为一个Kripke模型,φ为表示待验证性质的逻辑公式, 则K关于φ的反例是一个状态事件的有限交替序列ρ=s0e1s1e2s2…en-1sn-1ensn, 使得T(ei+1,si)=si+1和sn不满足φ同时成立, 其中: 0≤i 对于反例ρ=s0e1s1e2s2…en-1sn-1ensn, 事件序列e1e2…en刻画了模型所表示的程序引起ρ中状态从s0到sn变迁所执行的语句序列. 由于sn不满足φ, 如果把φ视为程序执行片段e1e2…en的后置条件, 则可通过计算最弱前置条件的方法获得该程序片段违反φ的一个最小谓词集, 从而定位产生反例的语句[11]. 下面根据事件结构给出最弱前置条件计算规则. 定义3事件序列最弱前置条件计算规则如下. 指派表达式序列: (2) (3) 事件序列: (4) (5) 式(2)给出了指派表达式的赋值规则, 它没有前提, 是一条公理, 表示如果程序在执行赋值语句x=E后有φ成立, 则程序执行x=E前必有φ[E/x]成立,φ[E/x]表示把φ中所有自由出现的x都用E替换后得到的公式, 其中φ是一个公式; 式(3)给出了指派表达式的复合规则, 它表示如果程序语句C1的后置条件和语句C2的前置条件相同, 则程序顺序执行C1和C2后φ成立, 蕴含程序顺序执行C1和C2前成φ立, 其中φ,η,φ是公式; 式(4)中g为事件e的守护条件, 表示若Wa为e指派动作的前置条件, 则g∧Wa为e的前置条件, 该规则的功能与文献[11]中assume语句最弱前置条件计算规则相同; 式(5)给出了事件复合规则, 与式(3)类似, 表示如果事件e1的后置条件与事件e2的前置条件相同, 则e1和e2顺序执行后W2成立, 蕴含e1和e2顺序执行前W1成立,W,W1,W2为公式. 文献[13]也使用了计算最弱前置条件的方法对反例进行分析, 但其目的是判定伪反例(判定反例的可行性), 而本文计算最弱前置条件的目的是分离出蕴含模型缺陷的谓词, 这与文献[10]中使用MAX-SAT求解机的目标相同. 给定关于Kripke模型K与公式φ的反例ρ=s0e1s1e2s2…en-1sn-1ensn, 令We(ei,φ)表示事件ei在后置条件φ下的最弱前置条件,Wa(ai,φ)表示ei的指派动作关于φ的最弱前置条件, 其中:ai为ei的指派动作;WE(Eij,φ)表示指派表达式Eij关于φ的最弱前置条件,Eij为ai中的指派表达式, 1≤i≤n, 1≤j≤k,k为ai中指派表达式的个数. 由规则2可得WE(Eij,φ)的计算公式为 WE(Eij,φ)=φ[uij/tij], (6) 其中:uij表示Eij的赋值表达式;tij表示Eij的赋值目标变量. 由规则3可得Wa(ai,φ)的计算公式为 Wa(ai,φ)=WE(Ei1,WE(Ei2,WE(Ei3,…,WE(Ei(ki-1),WE(Eiki,φ))))). (7) 由规则4可得We(ei,φ)的计算公式为 We(ei,φ)=gi∧Wa(ai,φ), (8) 其中gi为ei的守护条件. 由规则5可得ρ关于后置条件φ最弱前置条件的计算公式 W(ρ,φ)=We(e1,We(e2,We(e3,…,We(en-1,We(en,φ))))). (9) 由于反例中仅包含If语句和赋值语句, 不同于包含While语句的情况, 因此, 最弱前置条件计算过程不需要使用创造性的智力去构造不变量, 仅需要使用上推符号进行推理, 本质上是机械过程, 可使用程序自动完成. 定理1如果ρ=s0e1s1e2s2…en-1sn-1ensn是Kripke模型K上关于公式φ的反例, 则有s0不满足W(ρ,φ). 定理1表明了初始状态和反例最弱前置条件的不一致性, 本文通过从两者不一致性的证明中计算克雷格插值分离出反例失效的原因. 定义4给定公式对(φ1,φ2), 且φ1∧φ2不可满足, 则(φ1,φ2)的插值是一个满足下列条件的公式ψ: 1)φ1蕴含ψ; 2)ψ∧φ2不可满足; 3)ψ中的符号仅与φ1,φ2的公共符号有关. 这里的符号不包括∧,=等逻辑系统自身拥有的符号. 克雷格插值的一个重要性质是它反映了两个公式不一致的原因[14], 即φ1和φ2的不一致是由ψ导致的. 这是使用克雷格插值进行反例理解的基本依据和目的. 证明: 令atoms(φ)-atoms(WP(ρ,φ))表示出现在φ中但不出现在WP(ρ,φ)中的命题变量个数, 当atoms(φ)-atoms(WP(ρ,φ))=0时, 有atoms(φ)⊆atoms(φ)∩atoms(WP(ρ,φ)), 这种情况下显然有φ蕴含φ, 又由定理1知φ∧WP(ρ,φ)不可满足, 所以φ本身即为φ和WP(ρ,φ)的插值. 假设对任意的χ, 当atoms(φ)-atoms(WP(ρ,φ))=n时, 存在公式ψ为χ和WP(ρ,φ)的插值, 其中n∈N. 当atoms(φ)-atoms(WP(ρ,φ))=n+1时, 令φ′=φ[T/p]∨φ[F/ρ], 其中:p为属于φ但不属于WP(ρ,φ)的命题变量;φ[T/p]表示使用T替换φ中所有的p;φ[F/p]表示使用F替换φ中所有的p. 此时,φ蕴含φ′, atoms(φ′)-atoms(WP(ρ,φ))=n且φ′∧WP(ρ,φ)不可满足. 由atoms(φ′)-atoms(WP(ρ,φ))=n且φ′∧WP(ρ,φ)不可满足知存在公式ψ, 使得φ′蕴含ψ且ψ∧WP(ρ,φ)不可满足, 即ψ为φ′和WP(ρ,φ)的插值, 又由φ蕴含φ′及φ′蕴含ψ知φ蕴含ψ, 因此,ψ是φ和WP(ρ,φ)的插值. 定理2断言了反映φ与WP(ρ,φ)不一致原因插值的存在性. 因此, 可通过计算产生反例最弱前置条件与初始状态不一致的插值进行反例理解, 其优势在于: 在特定证明系统中,ψ能在线性时间内从φ∧WP(ρ,φ)的不一致性证明中获得. 文献[15]给出了从包含未解释函数符号的一阶逻辑公式不可满足证明中产生线性规模插值的方法及线性时间复杂度算法, 这为基于克雷格插值的反例理解提供了高效方法. 本文使用插值矢列法[16-17]从不可满足证明中计算插值. 定义5令Δ是一个文字集合,Δ↓φ表示Δ中的文字且这些文字中出现的命题变量也出现在φ中,Δ/φ表示Δ中的文字且这些文字中出现的命题变量不出现在φ中. 定义6(φ1,φ2)-〈Δ〉[ψ]是一个插值矢列, 当且仅当下列条件成立:φ1〈Δ/φ2〉, 并且φ2,ψ〈Δ↓φ2〉,ψφ1且ψφ2. 其中:φ1和φ2表示子句集合;Δ表示文字集合;ψ表示公式; 〈Δ〉表示Δ中包含的文字集合;ψφ1表示ψ中出现的变量都出现在φ1中.ψ是φ1和φ2的插值当且仅当〈Δ〉为空, 这也是插值矢列推导规则系统的最终目标. 用于引入子句的假设引入规则为 (10) (11) 下面给出两条用于解析子句的插值规则: 第一条规则用于解析不出现在φ2中的原子命题, 为 (12) 式(12)中p不出现在φ2中; 第二条规则用于解析出现在φ2中的子句, 为 (13) 式(13)中p出现在φ2中. (14) (15) 使用RES-A规则解析式(14)和(15)引入的子句: (16) 使用HYP-B规则引入φ2中的两个子句: (17) (18) 使用RES-B规则解析式(17)和(18)引入的子句: (19) 使用RES-B规则解析式(16)和(19)的解析结果: (20) 因此,q即为φ1和φ2的插值, 它反映了公式不一致的原因, 也是导致反例失效的原因. 有了克雷格插值, 即可通过寻找和插值ψ中谓词相关的状态定位引起错误的事件[11]. 如果反例ρ中的状态si满足ψ, 则si即为导致ρ失效的原因, 而ei直接解释了ρ迁移到ei的原因. 此外, 定义2给出的反例模型也使得本文给出的反例解释方法不需要为了避免如数组等不具备克雷格插值性质的量词无关理论而附加的额外工作. 基于克雷格插值的反例理解算法CICU(ρ,φ)步骤如下: 1) 由计算最弱前置条件给出的方法计算WP(ρ,φ); 2) 调用SAT求解机给出s0不满足WP(ρ,φ)的证明P; 4) 从克雷格插值中谓词与反例状态的对应关系确定引起反例失效的事件. 由于在反例状态序列中引入了引起状态变迁的事件序列, 与文献[6]中算法相比, CICU(ρ,φ)算法和文献[11]中算法都能直接把反例解释结果映射到引起软件失效的源码. 由算法的时间性能可见, 为了获得产生反例不可行原因的语法级证据, 文献[11]需要从不可满足公式中提取不一致谓词的最小集合, 该计算过程会对不可行公式中的所有文字进行逐个测试, 每次测试会触发一个SAT判定过程, 设SAT判定过程的时间复杂度为O(NSAT), 不一致公式长度为M, 则其计算最小不一致谓词集合的时间复杂度为O(NSAT×M); CICU(ρ,φ)算法获取反例初始状态不满足反例最弱前置条件的证明所需时间复杂度也为O(NSAT), 而CICU(ρ,φ)算法能在线性时间内从P中计算出克雷格插值, 令O(K)为计算克雷格插值所需的时间代价, 则CICU(ρ,φ)算法的时间复杂度为O(NSAT+K). 此外, 由计算结果正确性可见, 定理1确保了CICU(ρ,φ)算法的最弱前置条件推导能在有限步内计算出不一致公式, 为算法提取克雷格插值提供了有效输入, 定理2进一步断言了反例初始状态与其最弱前置条件克雷格插值的存在性. 因此, 定理1和定理2能保证CICU(ρ,φ)算法对反例失效原因的理解是正确的, 这与文献[14]的结论一致. 由于克雷格插值是不唯一的[14], CICU算法给出的结果与文献[9-11]一样都是近似解. 因此, 使用CICU(ρ,φ)算法和文献[11]的算法对反例进行理解时映射出的错误事件集都不完备. 本文实现了一个原型CICU算法用于验证引入克雷克插值后反例理解算法的时间性能, CICU的输入为LSVT中的BIC算法在医疗保险信息系统模型上产生的反例及其违反的性质, 插值计算使用了文献[18]的插值证明器. 实验环境: 处理器Pentium(R) Dual-Core E5200 2.50 GHz, 内存2 G, 操作系统为Ubuntu 11.04 i386, 程序运行环境NetBeans 6.9.1. 实验目的是在相同条件下对比使用逐次测试(TITU)和计算插值(CICU)的方法理解反例时的时间性能, 实验结果列于表1. 表1 TITU和CICU反例理解时间性能比较 表1列出了部分实验结果, 这些实验结果为分别在每条反例上使用TITU算法和CICU算法进行5次重复实验得出的数据. 由表1可见, CICU算法的时间性能明显优于TITU算法, 符合本文对算法的时间性能评价. 图1 公式长度对CICU时间性能的影响Fig.1 Influence of formula length on the time performance of CICU 此外, 两种算法的时间增长率均有一定程度的波动, 图1给出了CICU算法时间性能与公式长度变化的曲线. 由图1可见, 当不一致公式长度增加时, CICU算法的时间性能随之提高; 当公式长度减小时, CICU算法时间性能的提高趋势会相应减缓. 导致这种情况的原因是: 当公式长度较小时, TITU算法所消耗的时间代价显著降低, CICU算法相对TITU算法在时间性能上的提升空间也相应缩小. 总之, CICU算法时间性能提升的波动趋势与不一致公式长度变化趋势基本一致. 综上可见, 基于克雷格插值的反例理解算法能从反例最弱前置条件与初始状态的不一致证明中自动产生插值, 产生的插值是导致反例失效的原因. 本文使用的插值证明器能在线性时间内推导出插值, 使反例理解速度得到显著提升. 实验结果表明, CICU算法加快了提取反例失效原因的速度, 具有更好的可扩展性, 适用于理解更大规模的反例. 直接把反例理解结果映射到错误事件也能提高调试工作效率. [1] Clarke G O, Emerson E M. Model Checking [M]. Cambridge: MIT Press, 1999. [2] Ben-David S. Applications of Description Logic and Causality in Model Checking [D]. Waterloo: University of Waterloo, 2009. [3] Groce A, Chaki S, Kroening D, et al. Error Explanation with Distance Metrics [J]. International Journal on Software Tools for Technology Transfer (STTT), 2006, 8(3): 229-247. [4] Chechik M, Gurfinkel A. A Framework for Counterexample Generation and Exploration [J]. International Journal on Software Tools for Technology Transfer (STTT), 2007, 9(5): 429-445. [5] Griesmayer A, Staber S, Bloem R. Automated Fault Localization for C Programs1 [J]. Electronic Notes in Theoretical Computer Science, 2007, 174(4): 95-111. [6] Beer I, Ben-David S, Chockler H, et al. Explaining Counterexamples Using Causality [C]//Proceedings of the 21st International Conference on Computer Aided Verification. Berlin: Springer-Verlag, 2009: 94-108. [7] Halpern J Y, Pearl J. Causes and Explanations: A Structural-Model Approach [J]. The British Journal for the Philosophy of Science, 2005, 56(4): 843-887. [8] Suelflow A, Fey G, Bloem R, et al. Using Unsatisfiable Cores to Debug Multiple Design Errors [C]//Proceedings of the 18th ACM Great Lakes Symposium on VLSI. New York: ACM, 2008: 77-82. [9] Dershowitz N, Hanna Z, Nadel A. A Scalable Algorithm for Minimal Unsatisfiable Core Extraction [J]. Theory and Applications of Satisfiability Testing-SAT, 2006, 60: 36-41. [10] Jose M, Majumdar R. Cause Clue Clauses: Error Localization Using Maximum Satisfiability [C]//Proceedings of the 32nd ACM SIGPLAN Conference on Programming Language Design and Implementation. New York: ACM, 2011: 437-446. [11] WANG Chao, YANG Zi-jiang, Ivancic F, et al. Whodunit? Causal Analysis for Counterexamples [C]//Proceedings of the 4th international Conference on Automated Technology for Verification and Analysis. Berlin: Springer-Verlag, 2006: 82-95. [12] Graf S, Saidi H. Construction of Abstract State Graphs with PVS [C]//Proceeding of the 9th International Conference on Computer Aided Verification. Haifa, Israel: LNCS, 1997: 72-83. [13] Henzinger T A, Jhala R, Majumdar R, et al. Lazy Abstraction [C]//Proceedings of the 29th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. New York: ACM, 2002: 58-70. [14] Craig W. Linear Reasoning. A New Form of the Herbrand-Gentzen Theorem [J]. Journal of Symbolic Logic, 1957, 22(3): 250-268. [15] McMillan K L. An Interpolating Theorem Prover [J]. Theoretical Computer Science, 2005, 345(1): 101-121. [16] Henzinger T A, Jhala R, Majumdar R, et al. Abstractions from Proofs [C]//Proceedings of the 31st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. New York: ACM, 2004: 232-244. [17] Krajícek J. Interpolation Theorems, Lower Bounds for Proof Systems, and Independence Results for Bounded Arithmetic [J]. Journal of Symbolic Logic, 1997, 62(2): 457-486. [18] Jhala R, McMillan K L. A Practical and Complete Approach to Predicate Refinement [C]//Proceedings of the 12th International Conference on Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer-Verlag, 2006: 459-473.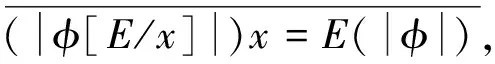
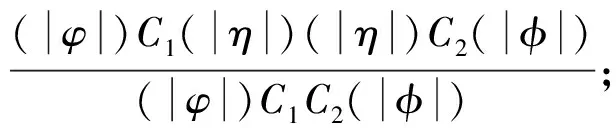
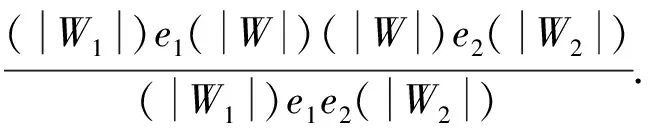
2 反例理解
2.1 计算最弱前置条件

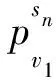

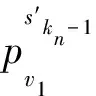

2.2 不一致分析

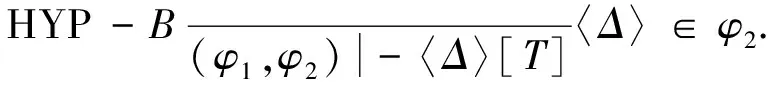


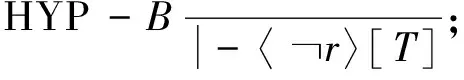
3 算法分析
4 实验结果