MCNP模拟卫星深层充电特征

周 庆, 王德军, 赵广义, 马玉刚, 赵宝奎, 易海云, 王振超, 牛璐莹

(1. 吉林大学 物理学院, 长春 130012; 2. 长春大学 继续教育学院, 长春 130022)

空间高能电子导致的介质深层充电严重威胁卫星安全和空间环境效应. 卫星中介质深层充电是指空间高能电子穿过卫星表面, 沉积于介质内部而构建的电场. 当介质内部沉积电荷产生的电场超过介质材料的击穿阈值时, 将发生放电现象, 干扰卫星正常工作的电子系统, 导致卫星运行失败[1]. 介质深层充电主要分为两方面:

1) 高能电子穿过卫星表面材料, 由于不同能量电子沉积于介质材料的不同深度, 从而在介质内部建立电场[2-4];

2) 卫星构件的电介质材料多为高分子聚合物, 介质受电子辐照其电导率发生变化[5-6], 从而影响介质内产生的电场.

引起介质深层充电的高能电子能量为0.1～10 MeV, 宇宙中电子能量主要按积分谱分布, 大部分能量为0.1～1 MeV. 因此卫星中介质深层充电主要受该部分能量电子影响.

文献[7-8]利用解析方法计算了平板和圆柱两种结构不同接地方法下的介质内电场分布; 文献[9]通过Geant4软件模拟了Teflon介质中的电荷输运过程. 本文利用MCNP软件模拟介质为环氧树脂的充电过程及不同能量电子对卫星介质内最大电场的影响.

1 模拟方法

图1 模拟结构Fig.1 Analog structure

1.1 模拟结构 卫星介质深层充电的模拟结构如图1所示. 通常聚四氟乙烯、 氟化乙丙烯和环氧树脂等高分 子聚合物作为卫星介质. 本文模拟的卫星介质为环氧树脂.

1.2 最大电场计算 若忽略电场和温度影响, 则

σ背部=σ0+σD=σ0+TФ背部,

其中:σ0为介质未受辐照下的电导率;T取决于介质材料的物理性能[10].

从介质层背部穿过的电子通量

Ф背部=Ф入射(x+d),

其中:x为屏蔽层厚度;d为进入介质内的深度. 由

e(Ф入射-Ф出射)=J背部=σ背部Emax

可得介质中最大电场

E=e(Ф入射-Ф背部)/σ背部.

2 模拟数据

本文计算了无屏蔽平板模型的环氧树脂最大电场. 模拟过程中, 入射电子采用积分谱的平均能量0.75 MeV, 电子通量为1×108cm-2·s-1(误差小于5%). 介质内最大电场随入射深度的变化关系如图2所示. 由图2可见, 介质内电场随介质厚度的增加先减小后增大, 当介质厚度为0.2 cm时, 电场达到最大值后趋于不变.

当不同电子能量入射时, 屏蔽物和介质第一个面的电子通量如图3所示. 由图3可见, 当电子能量大于1 MeV时, 介质第一个面比屏蔽层第一个面的电子通量多, 这是由于电子经过屏蔽层后, 打出较多次级电子进入介质所致. 当没有屏蔽层时, 介质内的最大电场出现负值, 如图2所示. 这是由于电子在介质内打出大量次级电子使得Ф出射增多, 最终Ф入射<Ф出射所致.

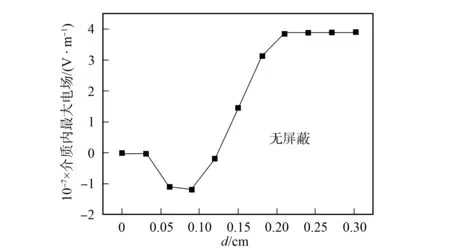
图2 介质内最大电场随入射 深度的变化关系Fig.2 Change of the biggest electric field in the medium vs penetration depth

图3 屏蔽层Al和介质环氧树脂 第一个面的电子通量Fig.3 Electron flux of shielding Al and medium epoxy at the first face

图4 介质内最大电场随屏蔽层厚度的变化关系Fig.4 Change of the largest electric field in the medium vs shielding thickness

当入射电子能量为0.75 MeV, 介质厚度为0.3 cm时, 介质内电场随屏蔽层Al厚度的变化关系如图4所示. 由图4可见, 随着屏蔽层厚度的增加, 介质内的电场先增大后减小, 当屏蔽层厚度约为0.04 cm时, 介质内电场达到最大值. 在曲线上升区间, 随着屏蔽层厚度的增加, 介质内电荷沉积增多, 因此电场增大, 当电子射程等于介质长度时, 电子穿出介质, 介质内的电场随屏蔽层厚度的增加而逐渐减小, 当屏蔽层厚度约为0.1 cm时, 电场达到最小值. 因此本文在模拟过程中均采用介质厚度为0.3 cm, 屏蔽层厚度为0.1 cm.

当厚度为0.1 cm的Al作为屏蔽层时, 介质内产生最大电场随介质厚度的变化关系如图5所示. 由图5可见, 当介质达到一定厚度后, 介质内的最大电场不再变化. 比较图5与图2可见, 对介质加屏蔽物后能缩小介质产生最大电场的厚度, 且最大电场在有屏蔽时较小.

当无屏蔽和有屏蔽层Al时, 介质0.3 cm处电场随入射电子能量增加的变化关系如图6所示. 由图6可见, 当电子能量小于1 MeV时, 入射电子几乎全部消耗在屏蔽层中, 即电荷均沉积在屏蔽层中, 有屏蔽介质内的电场远小于无屏蔽介质内的电场, 随着能量增加, 电子穿过屏蔽层, 沉积在介质内的电子增加, 电场增大, 当电子能量为1.5 MeV时, 电场达到最大, 此时有屏蔽比无屏蔽的电场大, 但该能量电子在积分谱中所占比例很小, 继续增加电子能量, 电子将穿出介质, 使介质中的电场下降.

图5 介质厚度对最大电场的影响Fig.5 Influence of medium thickness to the largest electric field

图6 介质0.3 cm处电场随入射电子能量的变化关系Fig.6 Change of electric field in the medium at the place of 0.3 cm vs incident electron energy

当屏蔽层Al的厚度不同时, 介质0.3 cm处电场随入射电子能量增大的变化关系如图7所示. 由图7可见, 随着屏蔽层厚度的增加, 介质内达到最大电场的电子能量逐渐增大, 即介质内的最大电场逐渐降低, 因此应选择较厚的屏蔽物. 当屏蔽层厚度为0.1 cm, 介质厚度为0.3 cm时, 不同屏蔽材料对介质内0.3 cm处的电场影响如图8所示. 由图8可见, Ag作为屏蔽层的保护作用最好.

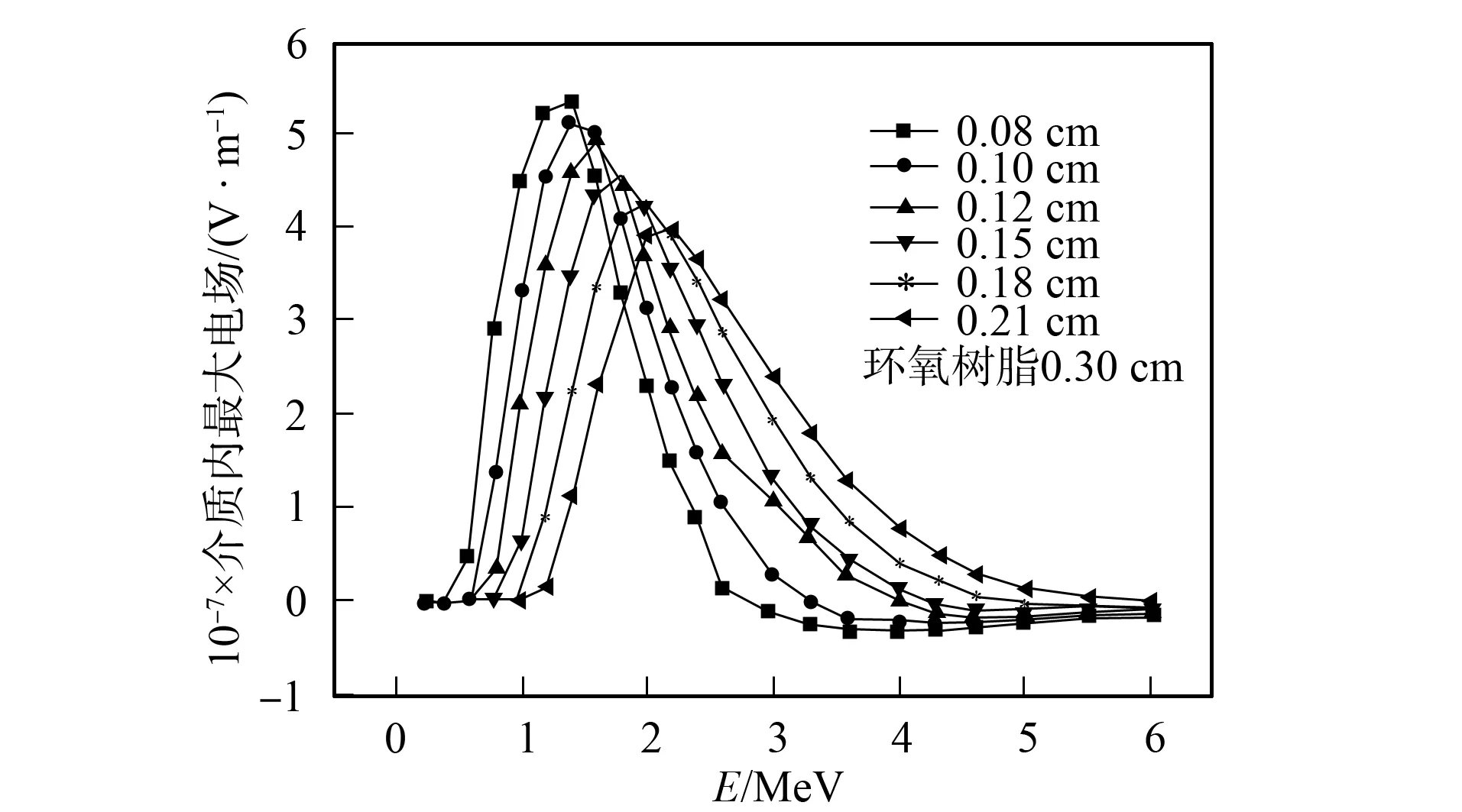
图7 不同屏蔽层Al厚度下介质中0.3 cm处 电场与电子能量的关系Fig.7 Relationship between electron energy and electric field in the medium at the place of 0.3 cm at different thickness of shielding Al

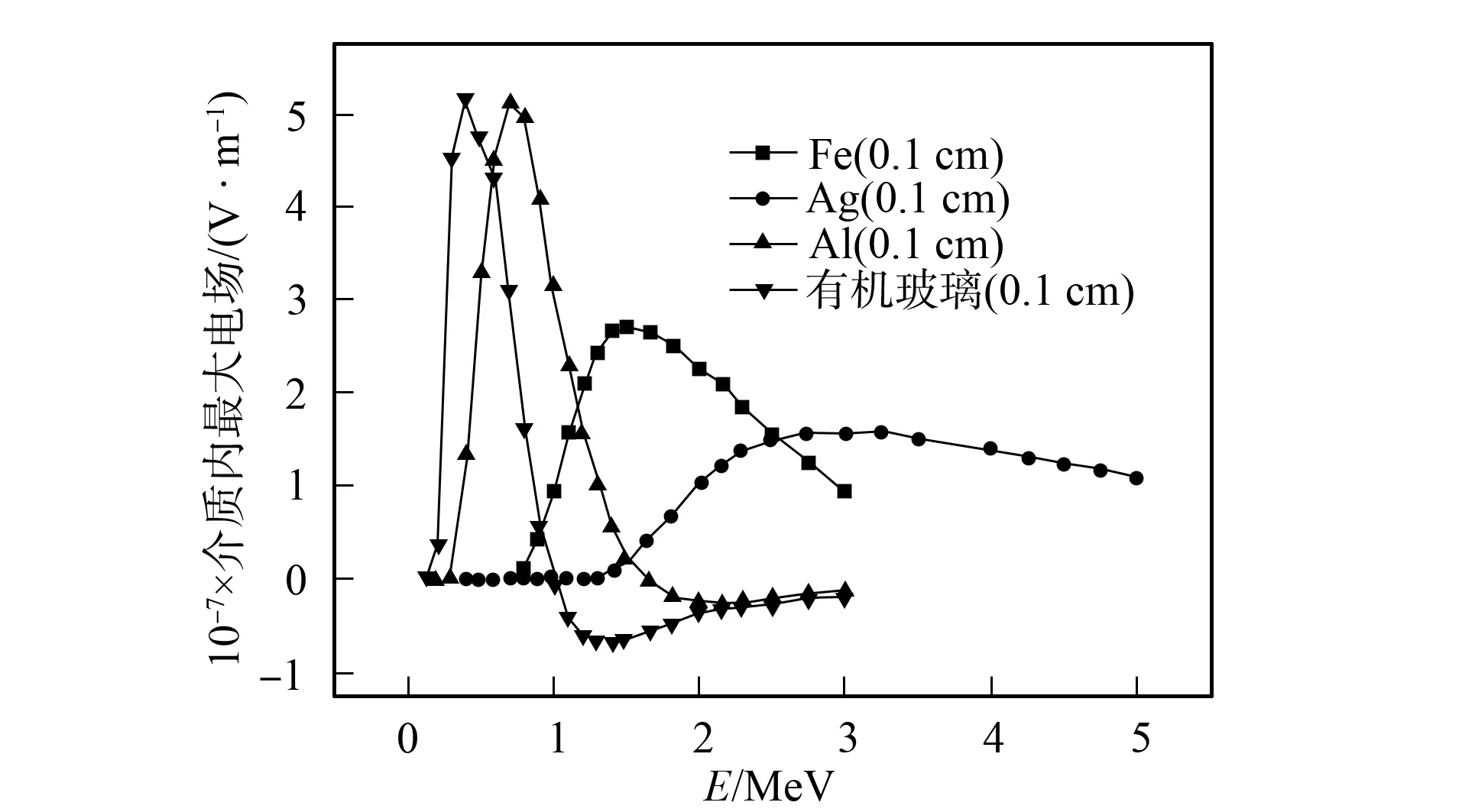
图8 不同屏蔽材料下电子能量与 最大电场间的关系Fig.8 Relationship of electron energy and the largest electric field in the different shielding materials

综上, 本文通过模拟卫星基本结构模型, 研究了电子在卫星中的运动情况和不同能量入射电子产生的电场与屏蔽体厚度的关系以及不同材料对卫星的保护作用. 结果表明: 当单能电子的能量为0.75 MeV时, 深层充电导致介质内最大电场随介质厚度的增加而增大, 介质厚度大于0.3 cm后, 介质内的最大电场不再随介质厚度的增加而增大; 当介质厚度一定时, 介质内最大电场随屏蔽层厚度的增加先增大后减小, 当屏蔽层厚度约为0.04 cm时, 介质内电场达到最大值; Ag作为屏蔽层的保护作用最好.

[1] HUANG Jian-guo, HAN Jian-wei. Analysis of a Typical Internal Charging Induced Spacecraft Anomaly [J]. Acta Physica Sinica, 2010, 59(4): 2907-2913. (黄建国, 韩建伟. 航天器内部充电效应及典型事例分析 [J]. 物理学报, 2010, 59(4): 2907-2913.)

[2] QUAN Rong-hui, ZHANG Zhen-long, HAN Jian-wei. Phenomenon of Deep Charging in Polymer under Electron Beam Irradiation [J]. Acta Physica Sinica, 2009, 58(2): 1205-1211. (全荣辉, 张振龙, 韩建伟. 电子辐照下聚合物介质深层充电现象研究 [J]. 物理学报, 2009, 58(2): 1205-1211.)

[3] QUAN Rong-hui, HAN Jian-wei, HUANG Jian-guo. Modeling Analysis of Radiation Induced Conductivity in Electrical Insulator [J]. Acta Physica Sinica, 2007, 56(11): 6642-6647. (全荣辉, 韩建伟, 黄建国. 电介质材料辐射感应电导率的模型研究 [J]. 物理学报, 2007, 56(11): 6642-6647.)

[4] GAO Bing-rong, HAO Yong-qiang, JIAO Wei-xin. A Study on Spacecraft Internal Charging with Monte Carlo Method [J]. Chinese Journal of Space Science, 2004, 24(4): 289-294. (高炳荣, 郝永强, 焦维新. 用蒙特卡罗方法研究卫星内部带电问题 [J]. 空间科学学报, 2004, 24(4): 289-294.)

[5] Ahrens T J, Wooten F. Electrical Conductivity Induced in Insulators by Pulsed Radiation [J]. IEEE Trans Nuc Sci, 1976, 23(3): 1268-1272.

[6] Fowler J F. Analytic Expression for Electrons Transmission in Dielectrics [J]. Proc Royal Soc, 1956, 23(6): 464-475.

[7] HUANG Jian-guo, CHEN Dong. A Study of Characteristic for Deep Dielectric Charging on Satellites [J]. Acta Physica Sinica, 2004, 53(3): 961-966. (黄建国, 陈东. 卫星介质深层充电特征研究 [J]. 物理学报, 2004, 53(3): 961-966.)

[8] HUANG Jian-guo, CHEN Dong. A Study of Deep Dielectric Charging on Satellites for Different Grounding Patterns [J]. Acta Physica Sinica, 2004, 53(5): 1611-1616. (黄建国, 陈东. 不同接地方式的卫星介质深层充电研究 [J]. 物理学报, 2004, 53(5): 1611-1616.)

[9] QIN Xiao-gang, HE De-yan, WANG Ji. Geant 4-Based Calculation of Electric Field in Deep Dielectric Charging [J]. Acta Physica Sinica, 2009, 58(1): 684-689. (秦小刚, 贺德衍, 王骥. 基于Geant 4的介质深度充电的电场计算 [J]. 物理学报, 2009, 58(1): 684-689.)

[10] HUANG Jian-guo, CHEN Dong. A Study of Deep Dielectric Charging on Satellites by Computer Simulation [J]. Chinese Journal of Geophysics, 2004, 47(3): 392-397. (黄建国, 陈东. 卫星介质深层充电的计算机模拟研究 [J]. 地球物理学报, 2004, 47(3): 392-397.)