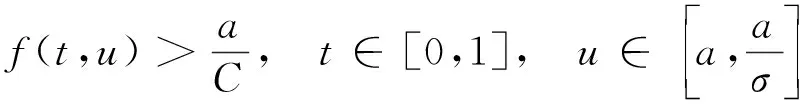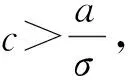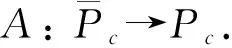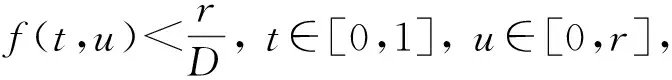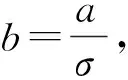一类Neumann边值问题正解的存在性
2013-12-03周韶林
周 韶 林
(西北师范大学 数学与统计学院,兰州 730070)
0 引 言
Neumann边值问题主要描述工程中边界点处梯度为零的物理现象,在工程领域应用广泛,目前已取得许多研究成果[1-8].蒋达清等[1]运用锥上的不动点定理研究了Neumann边值问题:

(1)
正解的存在性,在非线性项f满足超线性或次线性条件下获得了问题(1)至少有一个正解的存在性结果.其中:M<0为常数;f:[0,1]×[0,+∞)→[0,+∞)连续.孙建平等[4]运用Leggett-Williams不动点定理研究了问题(1)多个正解的存在性,在非线性项f满足适当的局部性条件下获得了问题(1)有3个正解的存在性结果.
对带一般微分算子Neumann边值问题:
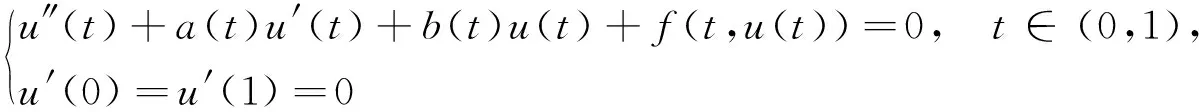
(2)
的研究目前尚未见文献报道.本文研究问题(2)正解及多个正解的存在性.显然,当a=0,b为常函数时,问题(2)即退化为问题(1).因此边值问题(2)比问题(1)更一般.
本文总假设:
(H1)a∈C[0,1],b∈C([0,1],(-∞,0));
(H2)f:[0,1]×[0,+∞)→[0,+∞)连续.
1 预备知识
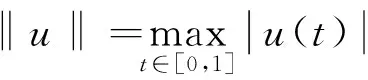
α(tx+(1-t)y)≥tα(x)+(1-t)α(y), ∀x,y∈P,t∈[0,1].

引理1设(H1)成立,φ(t),ψ(t)分别为初值问题:

(3)
和
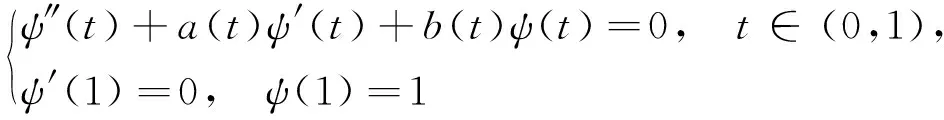
(4)
的解.则下列结论成立:
1)φ′(t)>0,t∈(0,1],且φ(t)>0,t∈[0,1];
2)ψ′(t)<0,t∈[0,1),且ψ(t)>0,t∈[0,1].
证明:仅证明1).2)的证明类似.
由φ′(0)=0,φ(0)=1可知φ″(0)=-b(0)>0.故存在δ∈(0,1),使得φ′(t)>0,t∈(0,δ).因此,φ在(0,δ)上严格单调递增.又因为φ在(0,δ)上是正的,所以由极大值原理可知,φ在(0,1)上不存在极大值,且φ在(0,1)上是非减的.
下证φ在[0,1]上严格单调递增.反证法.若不然,则存在t1,t2∈[0,1],满足t1
引理2设(H1)成立,h∈C[0,1].二阶Neumann边值问题:

(5)
等价于积分方程

(6)
其中:
(7)

(8)
证明:首先证明式(5)的唯一解可用式(6)表示.由引理1知,方程u″(t)+a(t)u′(t)+b(t)u(t)=0有两个线性无关解φ,ψ.由于


其次,验证式(6)定义的函数是式(5)的一个解.由式(6)有
从而
此外,容易验证

定义算子

不难验证A:C[0,1]→C[0,1]连续,u=u(t)是问题(2)的解当且仅当u(t)是算子A的不动点.
引理3设(H1),(H2)成立,则A(P)⊂P且A:P→P全连续.
证明:对u∈P,有
故A(P)⊂P.由Arzela-Ascoli定理易证算子A全连续.
2 主要结果
与文献[1]的证明类似,易得:
定理1设(H1),(H2)成立.若下列条件之一成立:
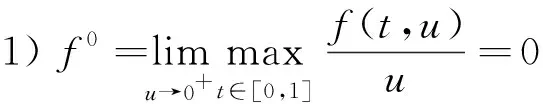

则问题(2)至少存在一个正解.
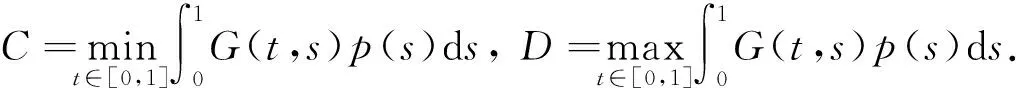
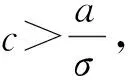
定理2设(H1),(H2)成立.若存在实数0 (9) (10) 成立;进一步,假设条件(H3)或(H4) 之一成立,则问题(2)至少存在3个正解. ∀t∈[0,1]. 因此,由式(10)可得 3) 验证若对任意的u∈P(α,a,c),‖Au‖>b,则α(Au)>a. (H5) 存在一列实数0 定理3设(H1),(H2),(H5)成立,则问题(2)存在无穷多个正解. 对任意的u∈∂Pa2k-1,‖u‖=a2k-1,有 故‖Au‖≥‖u‖,∀u∈∂Pa2k. [1] JIANG Da-qing,LIU Hui-zhao.Existence of Positive Solutions to Second Order Neumann Boundary Value Problems [J].J Math Res and Expos,2000,20(3):360-364. [2] SUN Jian-ping,LI Wan-tong.Multiple Positive Solutions to Second-Order Neumann Boundary Value Problems [J].Appl Math Compu,2003,146(1):187-194. [3] LI Xiao-yue,JIANG Da-qing.Optimal Existence Theory for Single and Multiple Positive Solutions to Second Order Neumann Boundary Value Problems [J].Indian J Pure Appl Math,2004,35(5):573-586. [4] SUN Jian-ping,LI Wan-tong,CHENG Sui-sun.Three Positive Solutions for Second-Order Neumann Boundary Value Problems [J].Appl Math Letters,2004,17:1079-1084. [5] Ahmed Bensedik,Mohammed Bouchekif.Symmetry and Uniqueness of Positive Solutions for a Neumann Boundary Value Problems [J].Appl Math Letters,2007,20:419-426. [6] CHU Ji-feng,SUN Yi-gang,CHEN Hao.Positive Solutions of Neumann Problems with Sigularities [J].J Math Anal Appl,2008,337:1267-1272. [7] SUN Yan,Yeol Je Cho,Donal O’Regan.Positive Solutions for Singular Second Order Neumann Boundary Value Problems via a Cone Fixed Point Theorem [J].Applied Mathematics and Computation,2009,210:80-86. [8] LI Zhi-long.Existence of Positive Solutions of Superlinear Second-Order Neumann Boundary Value Problem [J].Nonlinear Analysis,2010,72:3216-3221.