一类带有互相包含洞的区域与简单区域间拓扑关系的表示

李 健,朱佳斌,赵 慧

(吉林农业大学 信息技术学院,长春 130118)

空间推理[1-2]在地理信息系统(GIS)[3]等领域应用广泛.拓扑关系作为基本的空间关系,其相关表示直接影响空间分析和查询等应用中获取的信息量及有效性.拓扑关系的形式化描述主要包括4-交模型[4]、D9-交模型[5]、区域连接演算模型[6]和区域间拓扑关系的层次表达法等,其中具有典型性的是区域连接演算(region connection calculus,RCC)和交集模型.上述模型描述的空间对象多为两个简单区域,表达能力相对有限,而现实世界中的空间对象情况较复杂,对于带多个洞的区域与简单区域间的拓扑关系目前研究报道较少.本文提出一类带有互相包含洞的区域与简单区域间拓扑关系的表示可视为4个区域的应用.

1 互相包含洞的区域与简单区域间拓扑模型的建立

1.1 区域对象的定义

定义1若区域A包含区域B,则称B是A的洞,如图1所示.

定义2若区域A包含简单区域B,区域B又包含简单区域C,则称区域A,B,C构成一类带有互相包含洞的区域,如图2所示.

图1 简单带单洞区域Fig.1 Region with a hole

图2 一类带有互相包含洞的区域Fig.2 Region with holes of mutual inclusion

图3 一类带有互相包含洞的区域与一个简单区域Fig.3 Region with holes of mutual inclusion and a simple region

根据上述定义,本文对此类带有互相包含洞的区域与一个如图3所示简单区域间的拓扑关系进行研究,并将其划分为区域A,B,C,D四部分.由定义2可知,A包含B,B包含C,即A,B,C构成一类相互包含的洞,因此区域A和区域B,C间的拓扑关系是固定的.

1.2 12-交集模型

RCC理论[6-7]包括RCC-8和RCC-5,二者最大的区别是前者对边界敏感而后者对边界不敏感,对应拓扑关系的表示如图4所示.

图4 两个简单区域间的拓扑关系Fig.4 Topological relationship between two simple regions

研究表明,16-交集模型[8]是一类基于RCC5的处理4个区域间拓扑关系的模型,而对于16-交集模型所定义的0/1矩阵,其中有些位置上的元素取值不变,表现恒为0或恒为1,这是由固定拓扑关系导致的.由于区域A包含区域B和C,因此A的外部与B的内部或C的内部交集都为空,即A1∩B0和A1∩C0恒成立,如图5所示.

无论区域D的位置如何变动,区域A和区域B,C间的拓扑关系并不影响表示模型的区分,即下列情形都成立：A1∩B0∩C0∩D0=0,A1∩B0∩C0∩D1=0,A1∩B0∩C1∩D0=0,A1∩B0∩C1∩D1=0.因此可将16-交集模型进行改进,使之在满足能完备表示并区分一类带有互相包含洞的区域与简单区域间拓扑关系的条件下,减少矩阵元素个数,降低计算复杂度,实现模型优化.

本文将12-交集矩阵定义为

(1)

图5 交集情形Fig.5 Condition of regional intersections

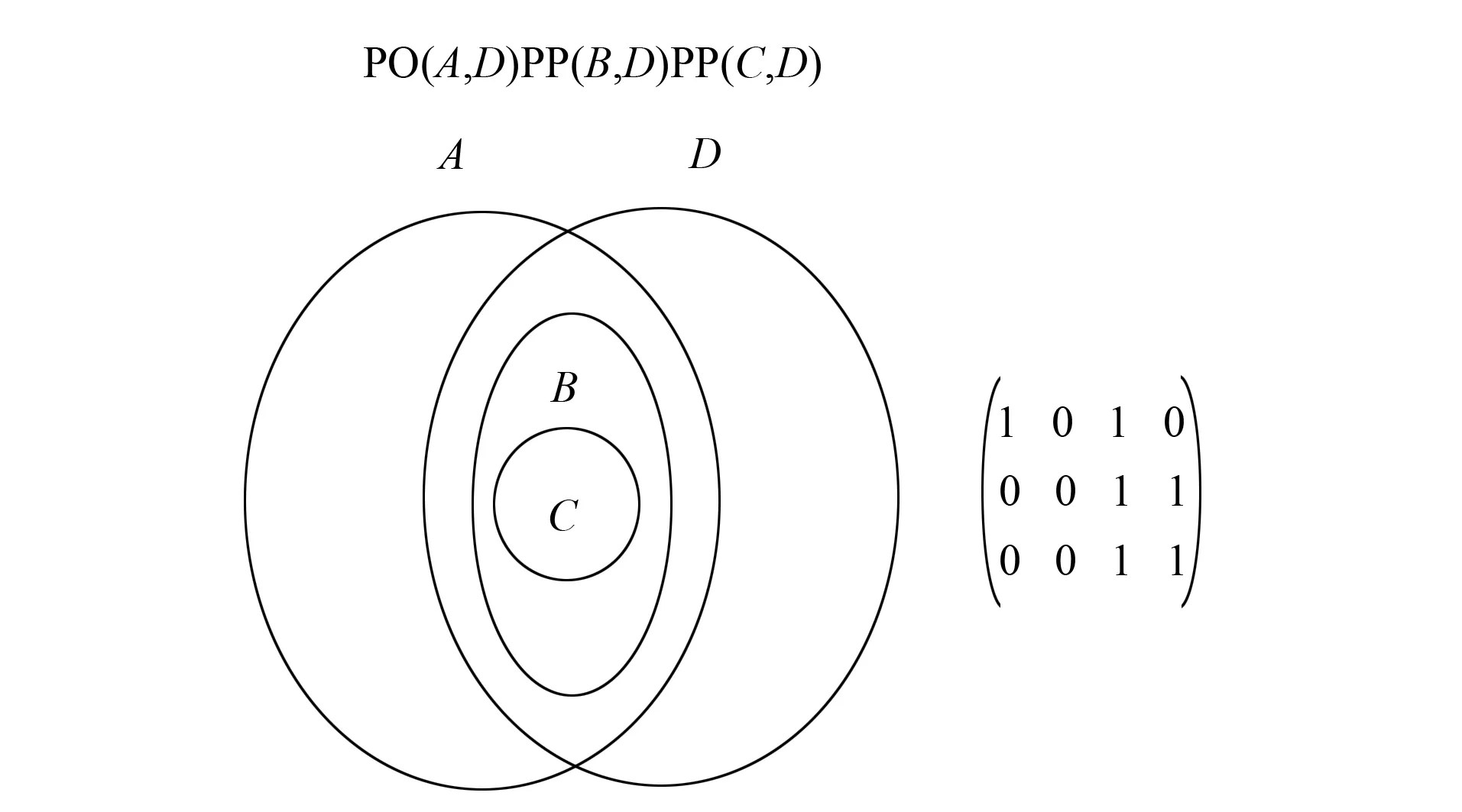
图6 可实现的12-交集矩阵Fig.6 Realizable 12-intersection matrix

其中每个12-交集矩阵都对应一个A,B,C,D之间的拓扑关系,如图6所示.16-交集模型解的搜索空间为216,而建立的12-交集模型解的搜索空间仅为212,极大降低了该问题的计算复杂性.

虽然理论上有212个12-交集矩阵,但并不是所有的矩阵都可实现.例如

(2)

即为不可实现的12-交集矩阵.式(1)中第12个元素A1∩B1∩C1∩D1,即4个区域的外部相交为空,这对于有界区域是不可能的.

2 约束条件及其表示

对于所有可实现的12-交集矩阵,必须满足如下约束条件.

约束条件1一个12-交集矩阵能对应一个可实现的6组拓扑关系,每组区域间的两两关系必须满足RCC5关系.

约束条件2对于简单有界区域,(AC)0∩(BC)0∩(CC)0∩(DC)0非空,即M1111=1.

约束条件3对于该类带有互相包含洞的区域与一个简单区域的4个部分A,B,C,D,有A包含B,B包含C,即B,C是区域A的洞,同时C是B的洞.

根据上述约束可得53种12-交集矩阵,这53种拓扑关系如图7所示.

图7 53种可实现的拓扑关系Fig.7 53 Topological relations and their schematics

定理1所有12-交集模型给出的带有互相包含洞的区域与一个简单区域间可实现的53种拓扑关系是两两互斥且完备的.

证明：因为由12-交集模型给出的带有互相包含洞的区域与一个简单区域间的212种拓扑关系(包括可实现的和不可实现的)是两两互斥且完备的,所以只需证明其中可实现的拓扑关系有且仅有53种.约束条件1和约束条件2是拓扑关系可实现的必要条件,通过这两个约束可得53种可能实现的拓扑关系,而图7表明可对这53种拓扑关系找到相应的具体实现情形,因此带有互相包含洞的区域与一个简单区域间的可实现的拓扑关系有53种,并为两两互斥且完备的.

综上所述,本文通过对16-交集矩阵进行改进得到了适合表示一类带有互相包含洞的区域与简单区域间拓扑关系的12-交集矩阵,给出了约束条件并得到了一类带有互相包含洞的区域与一个简单区域间的53种可实现的拓扑关系及53种拓扑关系图,进一步验证了53种拓扑关系矩阵都是可实现的,并证明了12-交集模型中基本关系是互斥且完备的.

[1] WANG Sheng-sheng,LIU Da-you.Knowledge Representation and Reasoning for Qualitative Spatial Change [J].Knowledge-Based Systems,2012,30:161-171.

[2] WANG Sheng-sheng,LIU Da-you.An Efficient Method for Calculating Qualitative Spatial Relations [J].Chinese Journal of Electronics,2009,18(1):42-46.

[3] Scott J,Lee L H.Designing the Low-Power M*CORETM Architecture [C]//IEEE Power Driven Microarchitecture Workshop.Piscataway:IEEE Computer Society,1998:29-33.

[4] Egenhofer M J,Franzosa R D.Point-Set Topological Spatial Relation [J].International Journal of Geographical Information System,1991,5(2):161-174.

[5] OUYANG Ji-hong,HUO Lin-lin,LIU Da-you,et al.Extended 9-Intersection Model for Description of Topological Relations between Regions with Holes [J].Journal of Jilin University:Engineering and Technology Edition,2009,39(6):1595-1600.(欧阳继红,霍琳琳,刘大有,等.能表达带洞区域拓扑关系的扩展9-交集模型 [J].吉林大学学报:工学版,2009,39(6):1595-1600.)

[6] Clarke B L.A Calculus of Individuals Based on “Connection” [J].Notre Dame Journal of Formal Logic，1981,22(3):204-218.

[7] Randell D,Cohn A.Modelling Topological and Metrical Properties in Physical Processes [C]//Proceedings of the First International Conference on Principles of Knowledge Representation and Reasoning.San Francisco:Morgan Kaufmann Publishers Inc,1989:357-368.

[8] LI Jian,OUYANG Ji-hong,WANG Zhen-xin.Representation for Topological Relations of Four Simple Regions [C]//The 2012 9th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD’12).Piscataway:IEEE Computer Society,2012:2961-2965.