回归模型参数检验及多克隆抗体效价的回归分析

彭毳鑫,杜泊船

(1.吉林师范大学 数学学院,吉林 四平 136000;2.吉林大学 生命科学学院,长春 130012)

线性回归模型在生物学、气象学、经济学及地理学等领域应用广泛.对于该模型的参数估计及相关假设检验方法的研究目前已取得了丰富的成果[1-8].经验似然方法是Owen[1]提出的一种非参数统计推断方法,与经典的或现代的统计方法相比,经验似然方法有很多突出的优点,如由经验似然方法构造的置信域除了具有变换不变性、域保持性及置信域的形状由数据自身决定外,还具有无需构造轴统计量等优点.本文利用经验似然方法研究响应变量Y与协变量X之间是否存在相关性的检验问题,建立了经验似然比统计量,并在原假设下获得了统计量的极限分布.

考虑一元线性回归模型:

Y=α0+α1X+ε,

(1)

其中:X是协变量;α=(α0,α1)T是未知参数向量;ε是随机误差项,满足Eε=0,Eε2=σ2.此外,假设ε和X相互独立.

1 主要结果

假设(Yi,Xi)(i=1,2,…,n)是来自模型(1)的一组观测样本,考虑如下检验问题:

1)H0:α1=0 vsH1:α1>0或2)H0:α1=0 vsH1:α1<0.

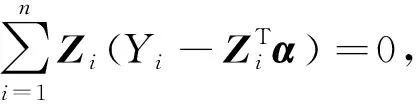
其中Zi=(1,Xi)T.进一步,令

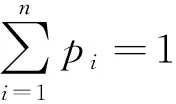
易证S1和S2是凸紧集,并且f(p)是一个凸函数.因此,存在

使得

f(p(1))=min{f(p):p∈S1},f(p(2))=min{f(p):p∈S2}.

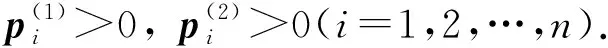
L(p(1))=max{L(p):p∈S1},L(p(2))=max{L(p):p∈S2}.

因此,对于检验问题1),可建立如下非参数似然比检验统计量

(2)

假设如下条件成立:

对于非参数似然比统计量R(α1),有如下结果:

定理1假设条件(H1)成立,则对于任意的t>0,

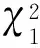
由定理1,对于检验问题1),可以利用检验统计量-2logR(α1)进行检验.

引理1假设条件(H1)成立.则当n→∞时,有

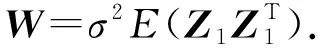
由独立同分布中心极限定理易证引理1成立.

定义

类似文献[9]中定理1的经验似然方法,可证明如下引理.

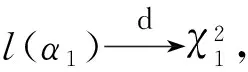
考虑如下优化问题(P):

其中f(x),gi(x)和hj(x)在开集X⊆n中有定义,并且可行域D={x:gi(x)≥0,i=1,2,…,m}是X的子集.进一步,令I(x*)={i:gi(x*)=0},有:

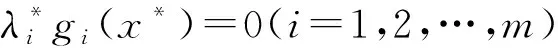
下面证明定理1.

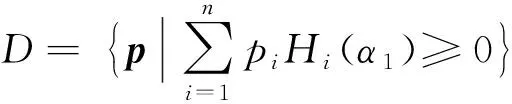
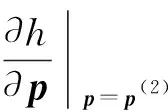
(3)

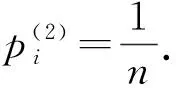
(4)

如果λ(2)<0,则g(p(2))=0.由式(3)可知

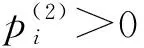
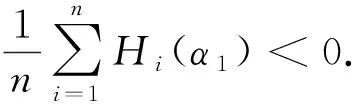
如果λ(2)<0,则

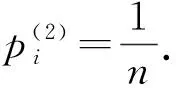
即定理1成立.

对于检验问题2),类似定理1易得如下结果:

定理2假设条件(H1)成立.则对于任意的t>0,

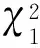
2 应 用

多克隆抗体是由多种B细胞产生的,可识别多种抗原决定簇的抗体集合.多克隆抗体由于具有可识别多个表位、可引起凝集反应和沉淀反应等优点,广泛应用于免疫学诊断领域.目前常用酶联免疫吸附剂测定法进行多克隆抗体的效价测定.该方法采用抗原与抗体的特异反应将待测物与酶连接,然后通过酶与底物产生颜色反应,利用连接于固相载体上的抗体和酶标抗体分别与样品中被检测抗原分子上抗原决定簇结合,形成固相抗体-抗原-酶标抗体免疫复合物.复合物的形成量与待测抗原的含量成正比.测定复合物中的酶催化加入底物后生成的有色物吸光度值(OD值),即可确定待测抗原含量.仍能产生阳性结果的最大稀释度,称为该抗体的效价.通过对多克隆抗体稀释倍数与OD值的回归分析,可建立估算抗体效价的数学模型,以提高抗原效价的准确性和工作效率.利用本文给出的检验方法,对稀释倍数与OD值之间的相关性进行检验,可得检验的p<0.01.检验结果表明,稀释倍数与OD值之间存在显著的相关性.进一步对实验结果数据进行拟合,可得稀释倍数与OD值之间的回归方程为Y=5 984.498-2 332.248X,其中:Y表示稀释倍数;X表示OD值.

[1] Owen A B.Empirical Likelihood Ratio Confidence Intervals for a Single Functional [J].Biometrika,1988,75(2): 237-249.

[2] Owen A.Empirical Likelihood for Linear Models [J].The Annals of Statistics,1991,19(4): 1725-1747.

[3] CHEN Song-xi.On the Accuracy of Empirical Likelihood Confidence Regions for Linear Regression Model [J].Annals of the Institute of Statistical Mathematics,1993,45(4): 621-637.

[4] CHEN Song-xi.Empirical Likelihood Confidence Intervals for Linear Regression Coefficients [J].Journal of Multivariate Analysis,1994,49(1): 24-40.

[5] WANG Qi-hua,Rao J N K.Empirical Likelihood-Based Inference in Linear Models with Missing Data [J].Scandinavian Journal of Statistics,2002,29(3): 563-576.

[6] SU Hai-yan,LIANG Hua.An Empirical Likelihood-Based Method for Comparison of Treatment Effects-Test of Equality of Coefficients in Linear Models [J].Computational Statistics and Data Analysis,2010,54(4): 1079-1088.

[7] ZHANG Juan,CUI Heng-jian.Empirical Likelihood Confidence Region for Parameters in Linear Errors-in-Variables Models with Missing [J].Journal of Systems Science and Complexity,2011,24(3): 540-553.

[8] QIN Yong-song,LI Ying-hua.Empirical Likelihood for Linear Models under Negatively Associated Errors [J].Journal of Multivariate Analysis,2011,102(1): 153-163.

[9] Owen A.Empirical Likelihood Ratio Confidence Regions [J].The Annals of Statistics,1990,18(1): 90-120.

[10] 盛昭瀚,曹忻.最优化方法基本教程 [M].南京: 东南大学出版社,1990.