NOVEL HIGH-SPEED FPGA-BASED FFT PROCESSOR
2013-12-02WangXudong王旭东XuWei徐伟DangXiaoyu党小宇
Wang Xudong(王旭东),Xu Wei(徐伟),Dang Xiaoyu(党小宇)
(College of Electronic and Information Engineer,Nanjing University of Aeronautics and Astronautics,Nanjing,210016,P.R.China)
INTRODUCTION
The fast Fourier transform (FFT)is one of the most popular algorithms in digital signal processing.It has been used in communications,radar and reconnaissance applications.Field programmable gate arrays(FPGAs)are attractive for accelerating FFT processing speed[1].
FFT implementations on FPGA have been performed by using distributed arithmetic[2-4],complex multipliers[5],coordinate rotation digital computer(CORDIC)algorithm[6],online arithmetic[7-8],and global pipeline architecture[9].However,there is no high speed FFT processor among them,which is critical for wideband system such as radar,software define radio(SDR)and reconnaissance[10].
Sharing single butterfly architecture is the most commonl use in FFT processors based on FPGAs[11-13].It basically consists of a unique butterfly,which performs all the operations of FFT,a two port random-access memory (RAM)to store the intermediate data,a memory with″twiddle factors″,address generators and control logic.For large transforms,the area of this architecture is considerably smaller than that of others,but in wideband systems,this is an improper architecture because it can not suit the required processing speed.
We propose a high speed 64-point FFT processor based on FPGA using a hybrid-parallel and pipeline architecture.The study is particularised to decimation-in-frequency (DIF)FFTs of 64-point length and an 8-bit word-size is considered.The whole processor is implemented using two parallel 8-point FFT and 8complex-multipliers between them.″Twiddle factor″addresses can be easily generated with counters.The address generation logic is very simple and does not limit the throughput of the system.Its performance is found to be suitable with 1GHz streaming input data,which is a highly effective option for wideband system.
1 HYBRID PARALLEL FFT ALGORITHM
To improve the system operation speed,a hybrid parallel FFT algorithm is used in this processor. Consider a direct Fourier transform(DFT)x(n)of dimension N[14]
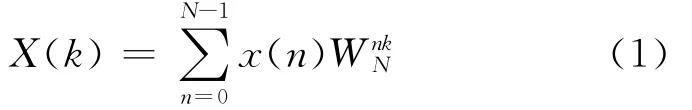
where WnkN=e-j2πkn/Nand k=0,…,N-1.If Nis the product of two factors,with N=N1*N2,we can redefine the indices n and k as follows:n=N1*n2+n1,k=N2*k1+k2,where n2=0,…,N2-1,n1=0,…,N1-1,k2=0,…,N2-1and k1=0,…,N1-1.
Then we can split WnkNas follows
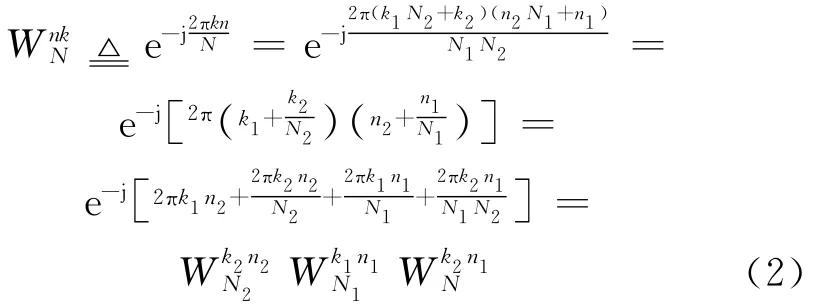
and we get
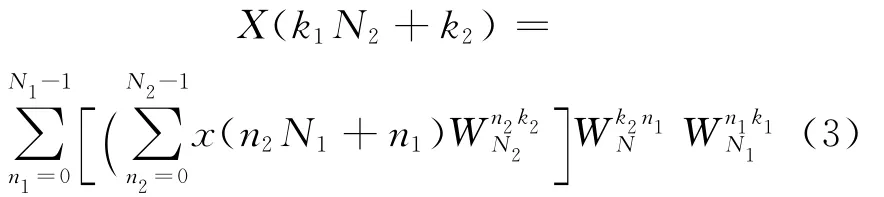
The Npoint DFT coefficients X(k)can be calculated by N1channels of N2point FFT in parallel.
2 FPGA IMPLEMENTATION AND SIMULATION
2.1 FPGA implementation
The structure of the routines implemented into FPGA is presented in Fig.1.
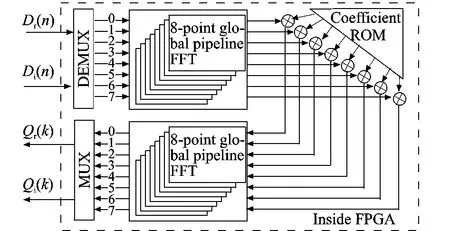
Fig.1 Internal structure of hybrid parallel FFT
Firstly,a DEMUX operation is used to deseries the input data,Dr(n),Di(n)into 8parallel channels.Secondly,aglobal pipeline 8-point FFT is employed to these parallel data.Thirdly,the outputs of the global pipeline FFT,Qr(k),Qi(k)are multiplied with 8complex coefficients from FPGA internal ROM.Finally,another global pipeline 8-point FFT processor is employed to output the 8complex multiplies.Afterwards,a MUX operation is used to make a serial output from FPGA.
The global pipeline 8-point FFT is illustrated in the form of a signal flow in Fig.2.The elementary operation is a two-point DFT butterfly,with the following form
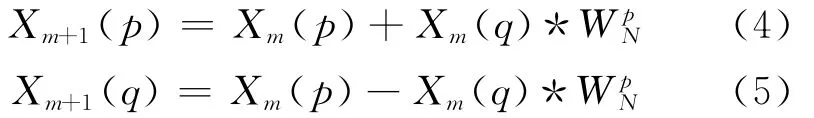
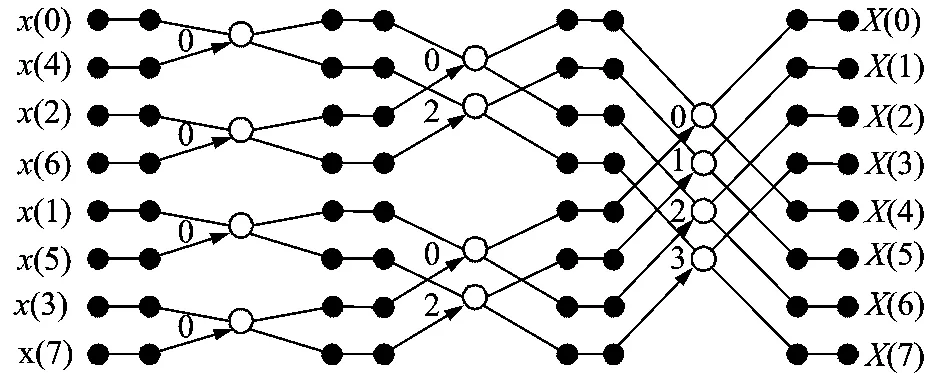
Fig.2 Global pipeline internal structure of FFT
The butterfly computation requires four real multiplications and six real additions/subtrations.The hardware used in this study exerts these computations using four fix-point multipliers and six fixpoint adders/subtracters,as shown in Fig.3.
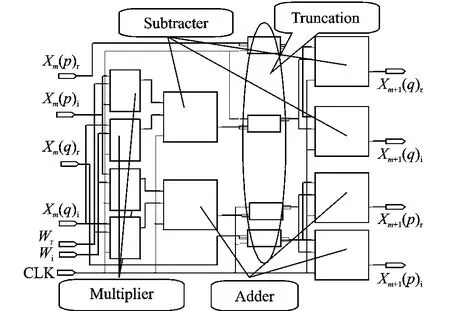
Fig.3 Basic butterfly structure
2.2 Simulation result
After the design entry of the respective blocks in the FFT processor,applying certain test patterns to verify the correctness of each block is functionally simulated.This level of simulation helps in testing the functionality of the design without the gate level delays.Simulation of the design after implementation is also conducted to obtain the delay associated with the FFT processor at the transistor level.This level of simulation takes more time compared to the functional simulation and gate level simulation.
This level of simulation is known as timing simulation.Functional verification of the designed FFT processor is performed by simulating the top level,Register transfer level (RTL),with the application of various test patterns using a test bench.Simulation consumes 24clock cycles to complete the 64-point FFT using the proposed hybrid parallel architecture,after the data has been applied.Synthesis and implementation of the design are proved to take very high speed and consume less power when implemented on an xc4vsx55device from the Xilinx family.The results of this time-efficient FFT processor are as shown in Fig.4and the synthesis report is shown in Table 1.In Fig.4,the input and the output are x(n)and X(k)in Eq.(1),respectively.
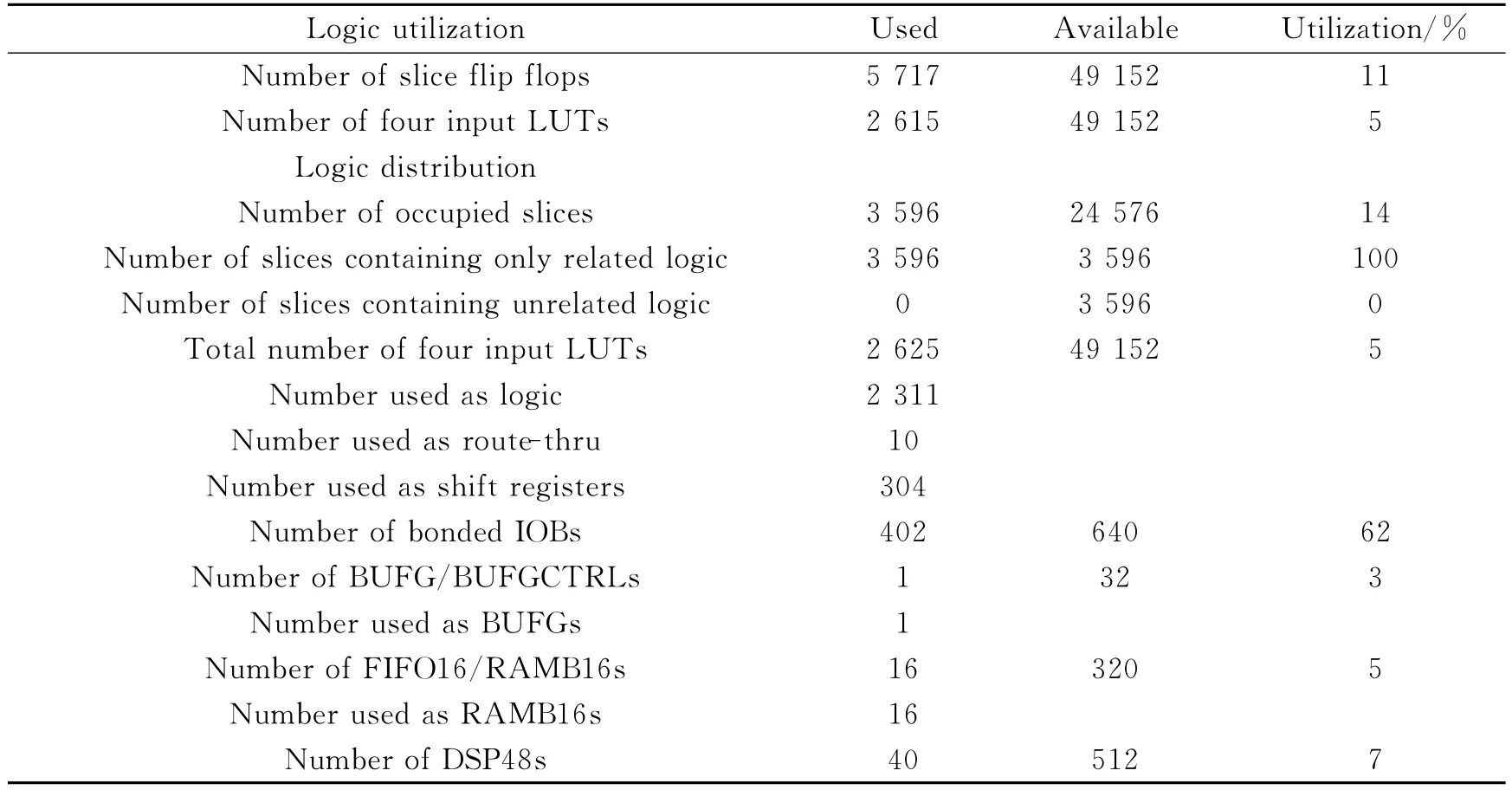
Table 1 Hardware description language synthesis report of FFT
The 64-point FFT is calculated using two global pipeline 8-point FFTs.The time-cost for the computation is 64ns(8periods)at 125MHz internal clock frequency.Thus the input and output data rates can be as fast as 1GHz,which is 8 times of the calculation speed inner FPGA chip.Fig.5shows the timing simulation result of this design at signal-to-noise ratio of 3dB in Model-Sim software and Fig.6plots the data in the wave using MATLAB software.
3 CONCLUSION
A 64-point high speed pipeline FFT processor for wideband system is designed,simulated,synthesized and implemented on FPGA.The whole design is implemented with very high speed hardware description language(VHDL).The architecture of this time-efficient FFT processor is given.VHDL is designed on Synplify software and simulation results are achieved on ModelSim software and then synthesis is processed on ISE software to get the logic level.The overall resulted design has been implemented in a Xilinx xc4vsx55FPGA.The approach presented here reduces the hardware complexity in FFT processor architectures and implements circuits more efficiently than global pipeline proposals do.Results indicate that the proposed time-efficient FFT processor performed with hybrid parallel structure gives up to 8times operation frequency than the Xilinx cores does[12].On the other hand,the area efficiency of the proposed 64-point FFT approach is 600%better than that of the global pipeline FFT processor proposed in Ref.[9].With our strategy,a time-efficient FFT processor is implemented to process data at a sample rate of up to 1Gsample/s using tolerant resources.
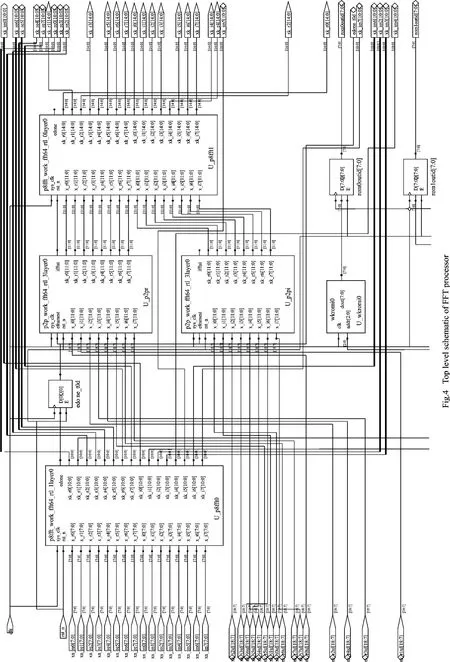

Fig.5 Simulation result of FFT processor
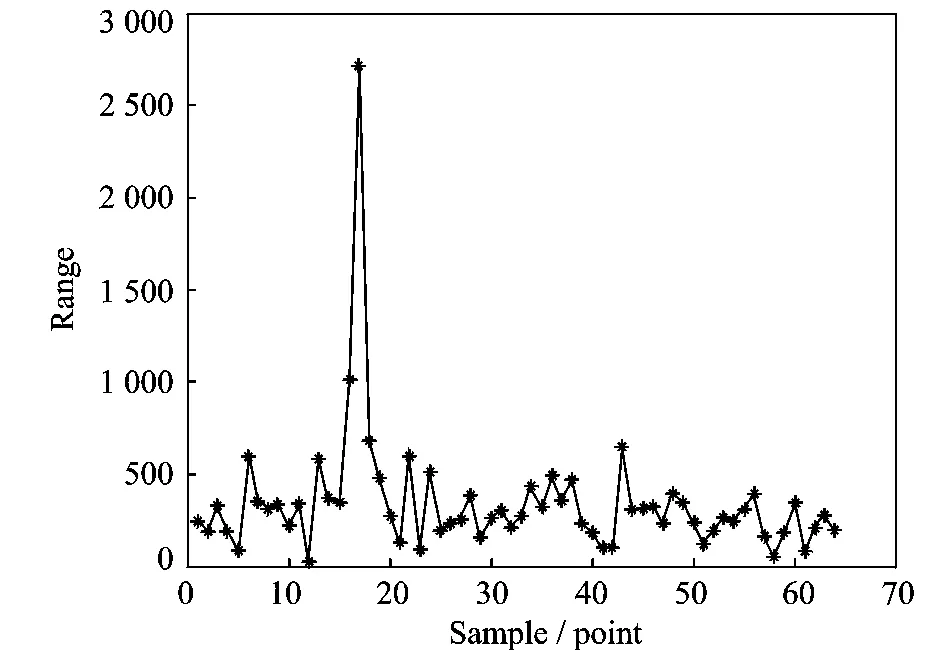
Fig.6 Wave data figure plotted in MATLAB
Acknowledgment
We appreciate Zhang Xiaofei′s gracious help.
[1] Chien C D,Lin C C,Yang C H,et al.Design and realization of a new hardware efficient IP core for the 1-D discrete Fourier transform[J].IEE Proc Circuits Dev Syst,2005,152(3):247-258.
[2] Yuan Zhou,Noras J M,Shepherd S J.Novel design of multiplier-less FFT processors[J].Signal Processing,2007,87(1):1402-1407.
[3] Nag S K,Verma H K.An efficient parallel design of FFTs in FPGAs[C]∥ Proc Int Conf on Signal Processing Applications and Technology (ICSPAT 98).Toronto,Canada:IEEE,1998:421-424.
[4] Sansaloni T,Perez-pascual A,Valls J.Distributed arithmetic radix-2butterflies for FPGA[C]∥Proc IEEE International Conference on Electronics,Circuits and Systems (ICECS 2001).Malta:IEEE,2001:521-524.
[5] Lo Sing-Cheng,Ali Miri,Tet Hin-yeap.Efficient FPGA implementation of FFT based Multipliers[C]∥18th Proc IEEE CCECE/CCGEI.Saskatoon,Canada:IEEE,2005:1300-1303.
[6] Banerjee A,Dhar A S,Banerjee S.FPGA realization of a CORDIC based FFT processor for biomedical signal processing[J].Microprocessor and Microsystems,2001,25(1):131-142.
[7] Perez-Pascual A,Sansaloni T,Valls J.On-line radix-2butterflies on FPGA[C]∥Proc WSES International Conference on Speech,Signal and Image Processing.Singapore:IEEE,2002:2201-2205.
[8] Perez-Pascual A,Sansaloni T,Valls J.FPGA based radix-4butterflies for HiperLAN2[C]∥Proc IEEE International Symposium on Circuits and Systems(ISCAS 2002).Arizona,USA:IEEE,2002(III):277-280.
[9] Szadkowski Z.16-point discrete Fourier transform based on the Radix-2FFT algorithm implemented into cyclone FPGA as the UHERC trigger for horizon-tal air showers[C]∥Proc of the 29th ICRC.Mexico:IEEE,2005:201-205.
[10]Sanchez M,Garrido M,Lopez-Vallejo M,et al.Digital channelised receivers on FPGA platforms[C]∥Proc IEEE International Radar Conference.Virginia,USA:IEEE,2005:816-821.
[11]Mou Shengmei,Yang Xiaodong.Design of a highspeed FPGA-based 32-bit floating-point FFT processor[C]∥IEEE Eighth ACIS International Conference on Software Engineering,Artificial Intelligence,Networking,and Parallel/Distributed Computing.Uru-guay:IEEE,2007:84-87.
[12]Xilinx Inc.Xilinx logicore:fast fourier transform[EB/OL].(2010-01-01)[2013-03-10].http://www.xilinx.com.
[13]Sansaloni T,Perez-Pascual A,Torres V,et al.Scheme for reducing the storage requirements of FFT twiddle factors on FPGAs[J].Journal of VLSI Signal Processing,2007,47(1):183-187.
[14]Oppenheim A V,Schafer R W,Buck J R.Discretetime signal processing[M].Englewood Cliffs,NJ:Prentice-Hall,1999:484-488.
猜你喜欢
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- EFFECTS OF INHALED TiO2NANOTUBES ON LUNG TISSUE AND SERUM BIOCHEMICAL INDEXES OF MICE
- ENERGY-SAVING MATCHING STRATEGY AND EXPERIMENTAL STUDY OF PUMPING SYSTEM FOR TRUCK-MOUNTED CONCRETE PUMP
- SPATIAL REGULARIZATION OF CANONICAL CORRELATION ANALYSIS FOR LOW-RESOLUTION FACE RECOGNITION
- SOFT IMAGE SEGMENTATION BASED ON CENTER-FREE FUZZY CLUSTERING
- PREDICTION OF SURFACE ROUGHNESS FOR END MILLING TITANIUM ALLOY USING MODIFIED PARTICLE SWARM OPTIMIZATION LS-SVM
- EXPERIMENTAL INVESTIGATION ON R134AAIRBORNE VAPOR-COMPRESSION REFRIGERATION SYSTEM
