基于非达西渗流的砂井地基径向固结解

李文翔，刘曙光，蔡 奕，阮春生

（1.同济大学 土木工程学院，上海200092；2.中交第三航务工程勘察设计院有限公司，上海200032）

在沿海地区的工程建设中，经常会遇到含水量大、承载力低、压缩量高的软土地基.通过在软土地基中打设砂井可以改变土体的排水路径，形成砂井地基，促使土体提高固结速率从而达到增加地基承载力、控制工后沉降等目的.1948 年Barron［1］首先提出了砂井轴对称固结理论，此后Hansbo等［2］给出了等应变条件下考虑井阻和涂抹作用的砂井地基固结解，谢康和等［3］推导了等应变条件下考虑径竖向组合渗流的沙井固结方程并得到了解析解.砂井固结理论在不断完善［2－8］.

但是，这些成果大多是在假定土层中孔隙水渗流特性符合达西定律的基础上取得的.大量研究证明［5－8］，在软黏土中渗流特性往往会偏离达西定律，表现出非线性和存在起始水力梯度的非达西特征.软黏土中常含有大量的亲水物质，土颗粒周围因存在结合水而呈现黏滞性，只有克服结合水的黏滞阻力后，渗流才会发生.而克服此黏滞力所需的水力梯度，称为起始水力梯度.由于存在起始水力梯度，使得软黏土中的渗流特性偏离达西定律，进而会对软黏土地基的固结性状产生影响.齐添等［4］利用GDS固结仪对萧山黏土进行了固结渗透联合试验，研究了渗流速度与水力梯度的非线性关系，结果表明，黏土中的渗流呈现出非达西特性.Hansbo［5］在实验的基础上提出了指数形式的渗流模型，并将其引入砂井地基固结理论刘忠玉等［6－7］、周琦等［8］对考虑起始水力梯度时软黏土的固结情况进行了研究，但都未给出显式解.

本文将考虑起始水力梯度的非达西渗流模型引入了砂井地基固结理论，建立了相应的控制方程，并通过推导给出了其显式解.最后通过计算分析，研究了考虑起始水力梯度时砂井地基的固结性状.

1 模型的建立

1.1 计算简图及基本假定

砂井地基固结计算简图如图1所示.图中l为砂井计算长度，H为土层的厚度，单面排水时l＝H.本文不考虑涂抹作用，re为砂井的影响区土体半径，rw为砂井半径，de为砂井的影响区土体直径，kh为地基水平渗透系数，kv为地基竖向渗透系数，kw为砂井渗透系数，q0为瞬时施加并在固结过程中保持不变的均布荷载.r，z分别为径向和竖向坐标.

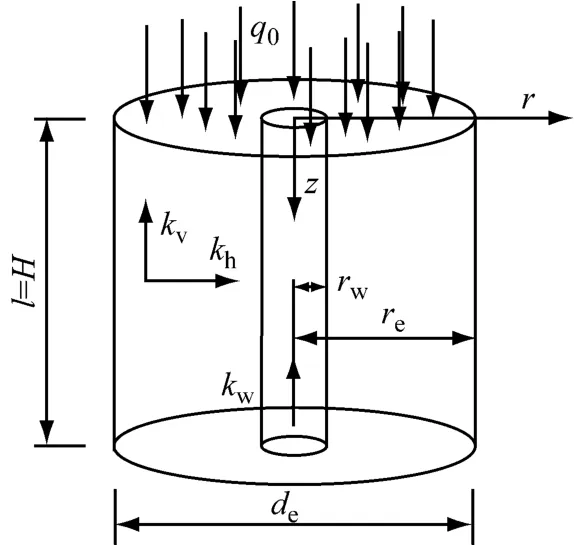
图1 砂井地基固结计算简图Fig.1 Schematic diagram for consolidation computation of sand drains foundation

采用如图2所示的考虑起始水力梯度的渗流模型取代达西渗流模型，其数学模型可以表示为

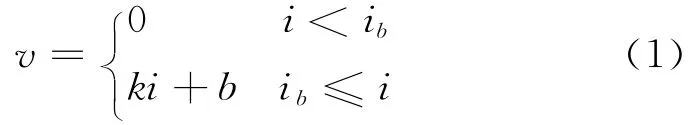
式中：v为孔隙水渗流速度；i为水力梯度；ib为起始水力梯度；k为图中直线的斜率，即土体的渗透系数；b＝－kib.除此之外，采用与传统砂井固结理论相似的假定，即

（1）等应变条件成立，即假定在砂井影响区范围内同一水平面上各点的土体竖向变形相等.

（2）砂井地基固结过程中，径向和竖向渗流可以分别单独考虑.本文只考虑径向渗流情况，且认为固结开始时渗流前锋面已到达re.

（3）土体完全饱和，且孔隙水的渗流情况服从式（1）表示的非达西渗流模型.

（4）在任一深度处，从土体中沿井周流入砂井的水量等于从砂井流出的水量增量.

（5）H深度处为不透水土层，且认为影响区径向re外也为不透水区域.

（6）除了渗透系数之外，砂井与土体的其他性质相同.

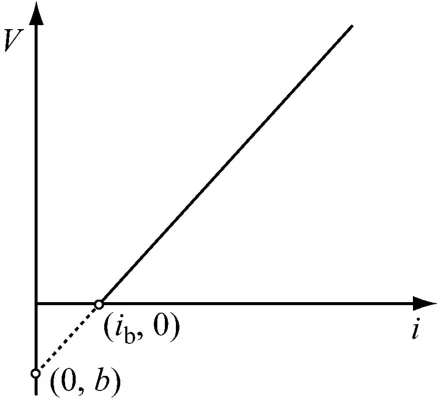
图2 考虑起始水力梯度的非达西渗流模型Fig.2 The non－Darcy seepage model with a consideration of initial hydraulic gradient

1.2 控制方程及定解条件

根据基本假定［1－3，9］，用式（1）代替达西定律的公式，经过推导可以得到考虑起始水力梯度的砂井地基固结控制方程为

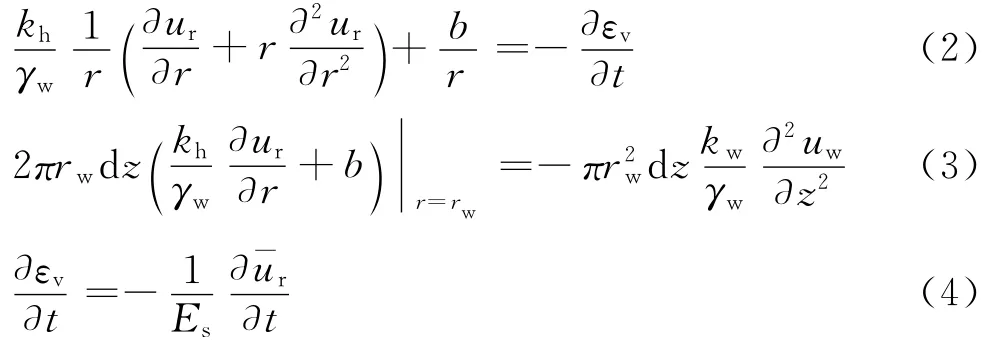
式中：γw为孔隙水重度；εv为仅考虑径向渗流时砂井影响区内土体任一点的体积应变；ur为影响区内土体中任一点的孔压；uw为砂井内任一深度的孔压为影响区内土体中任一深度的平均孔压；t为时间；Es为土体压缩模量.其中

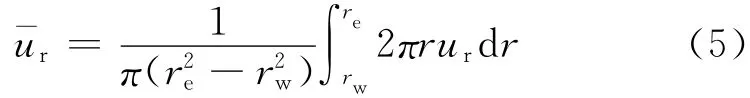
模型的定解条件为

其中u0为施加q0后在土体中产生的初始孔压.

把控制方程（2），（3），（4）和定解条件①，②，③，④，⑤结合在一起，就构成了考虑起始水力梯度的砂井地基固结的定解问题.

2 方程求解

对式（2）两边关于r积分，并利用定解条件②，可以得到

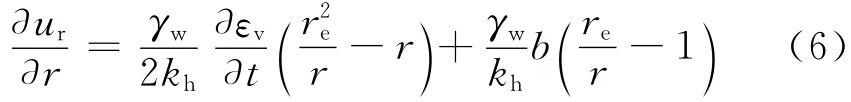
将式（6）代入式（3），并整理可得

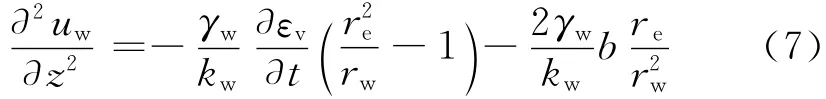
对式（6）两边再次关于r积分，并利用定解条件①，可以得到

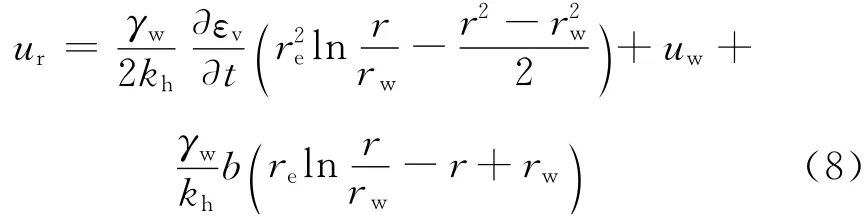
将式（8）代入式（5），并计算整理可得

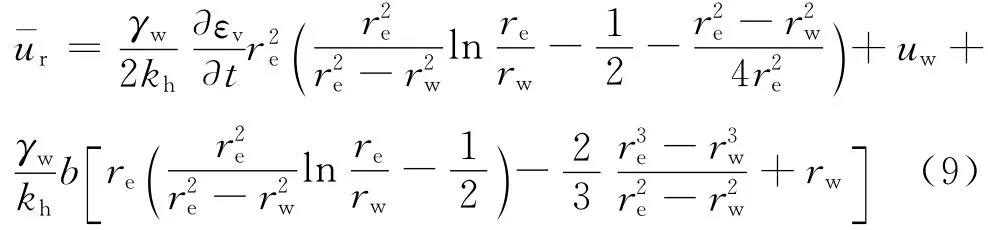
为了简化方程，可以设则式（9）可以简写为

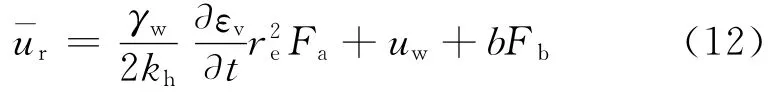
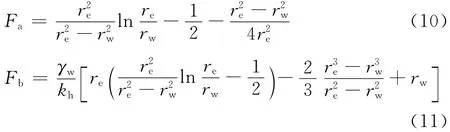
联立式（4），（7），（12），可以得到可以设

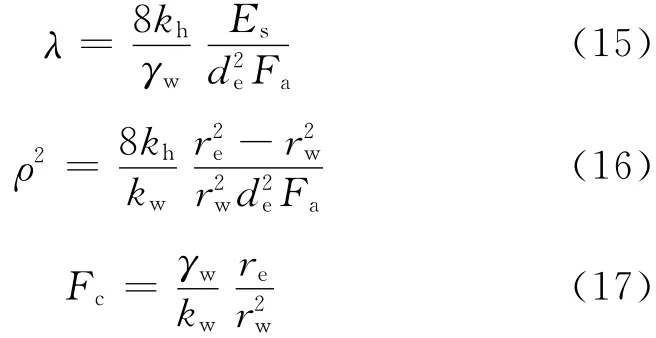
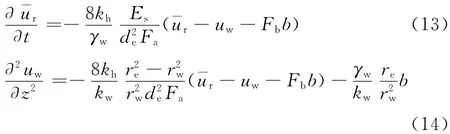
则式（13），（14）可以写为

式（19）两边对t求导数，可得

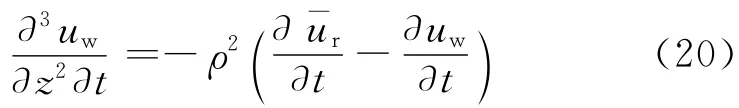
并且由式（19）可得

将式（21）代入式（18）可得

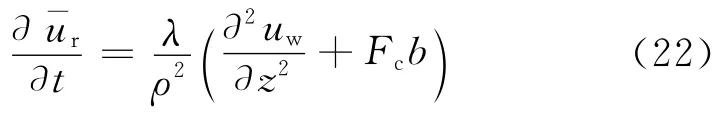
再将式（22）代入式（20），整理可得

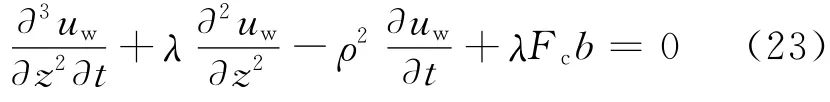
可见，式（23）为非齐次偏微分方程，不能直接通过分离变量法求解，需要对其进行代换处理.令

式（23）可以改写为

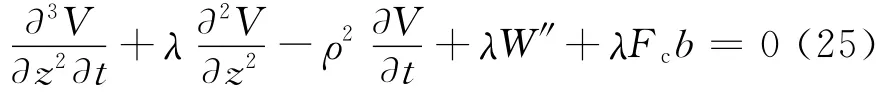
同时，定解条件③，④可写为

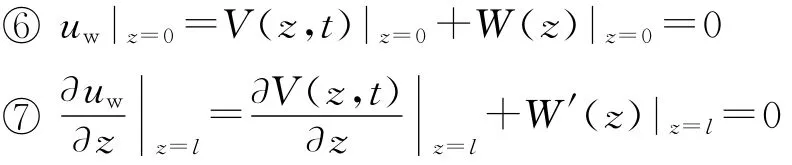
选取W（z）使得其满足

可以解得

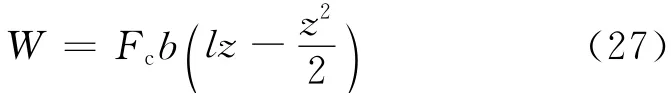
而对于V（z，t）则有

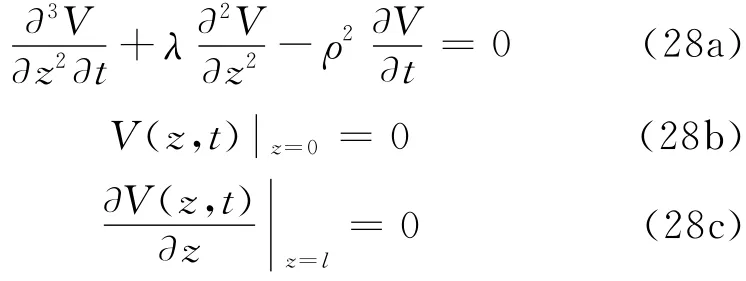
可以使用分离变量法对其求解.设

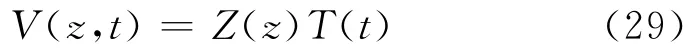
将其代入式（28a），则有

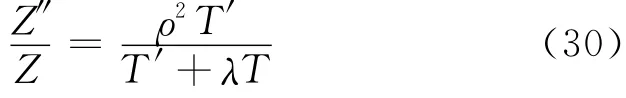
设式（30）比值为－η2，由于左式不依赖于t，右式不依赖于z，因此－η2既不依赖于t又不依赖于z，它只能是常数，其数值待定.于是有

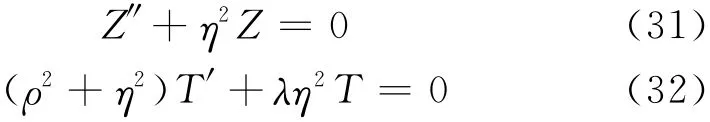
分别对式（31），（32）求解，可以得到

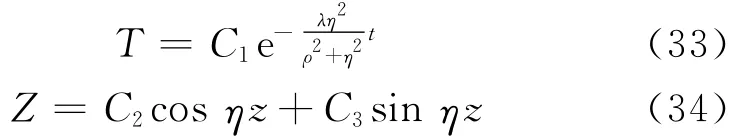
式中：C1，C2，C3为待定系数.将式（33），（34）代入式（29）有式中：A，B为待定系数，其中A为C1或C3，B为C1或C2.

利用求解条件（28b），（28c），可得

为了使得V（z，t）有非零解，应当有

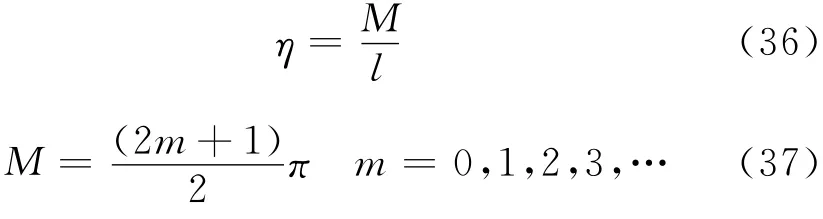
于是有

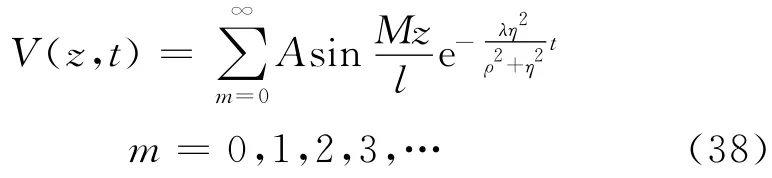
将式（27），（28）代入式（24），有

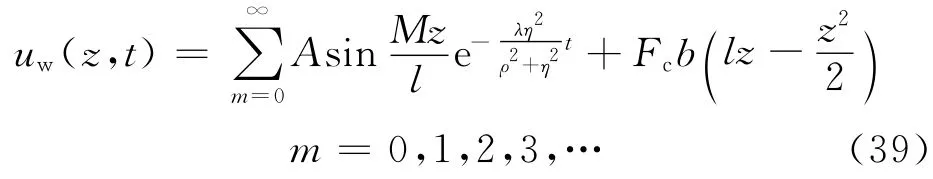
将式（39）代入式（19）可得

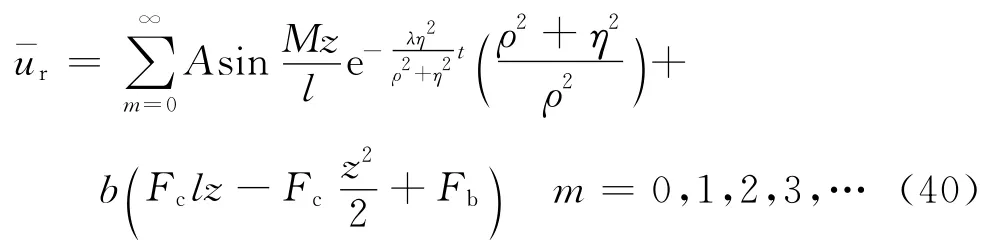
由式（40）和初始条件⑤，可得

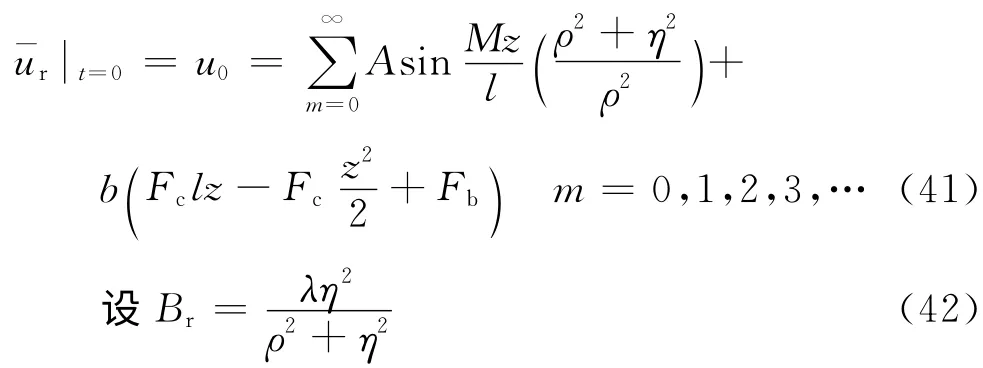
再利用函数系

在区间［0，l］上的正交性质，可得

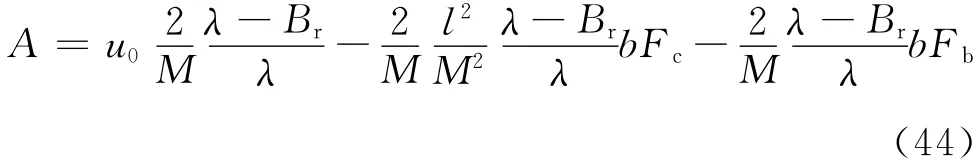
联立式（4），（8），（39），（40），（44）可得

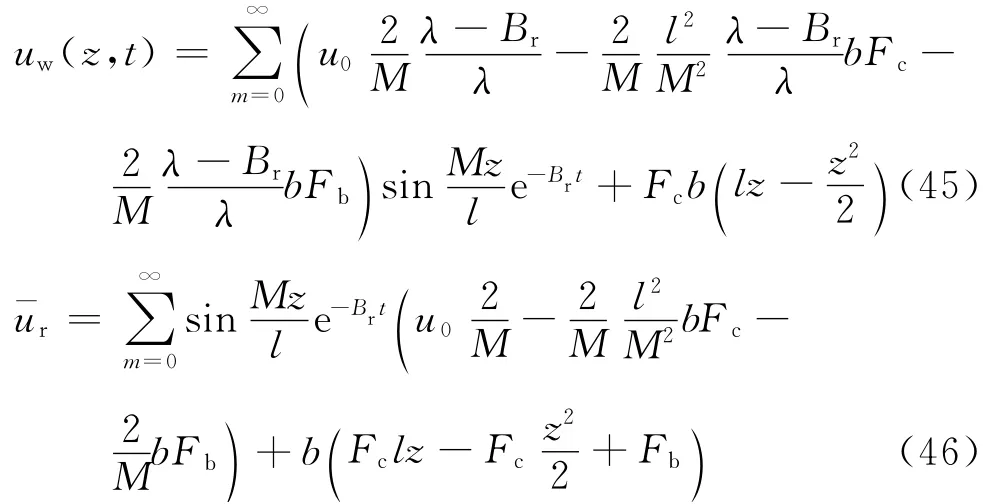
地基任一深度的径向固结度Ur为

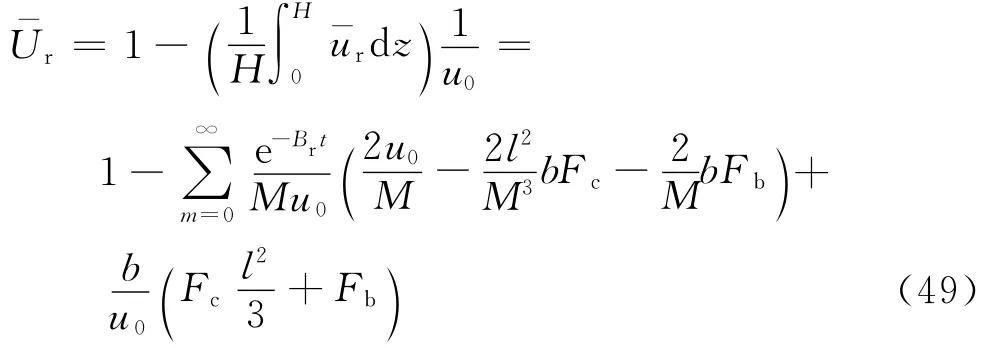
若不考虑井阻作用，kw→∞，Fc＝0，Br＝λ，并由级数理论，可以证明［3］

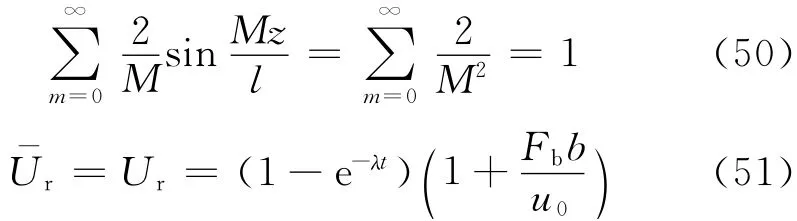
式（45），（46），（47），（48），（49），（51）即为本文的解.可见，若将b＝0 代入，本文的解与文献［3］和文献［10］的结果相同，即本文解可以退化为传统砂井地基固结理论解.

3 算例分析

由本文解的形式可以看出，考虑起始水力梯度的砂井地基固结解与传统理论解的差异大小，会受到参数b，u0和re的影响.根据文献［11－12］的研究，起始水力梯度的取值范围在0～13之间.图3为不同的起始水力梯度下，砂井地基的固结曲线.考虑起始水力梯度时，砂井地基在经历长时间固结后，其最终的应力固结度将不会达到100%，而是会稳定在一个小于100%的数值上.最终的固结度会随着起始水力梯度的增加而减小.图3中，当ib分别为2，4，6，8，10时，最终固结度分别为87%，75%，62%，50%，37%.

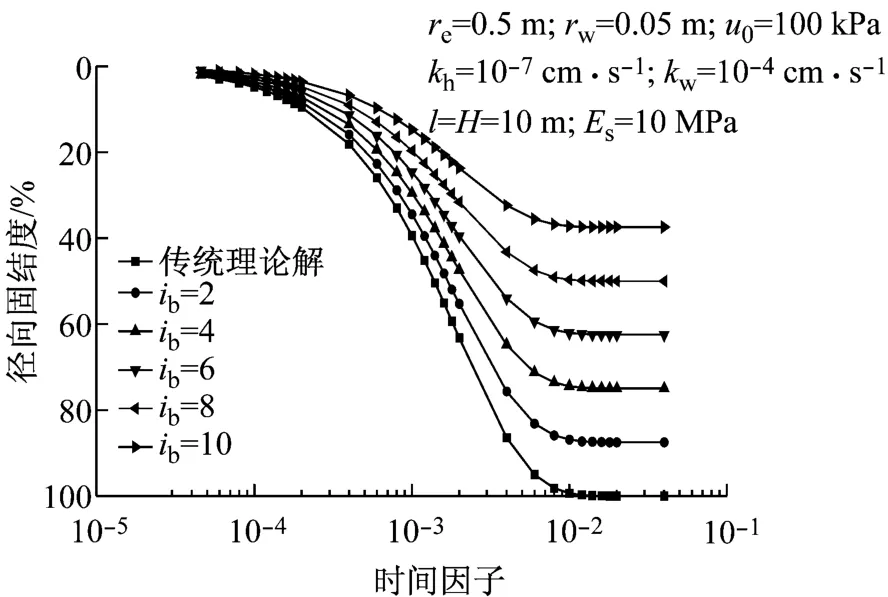
图3 起始水力梯度对固结度的影响Fig.3 Influence of initial hydraulic gradient on consolidation rate

图4为取不同的影响区半径情况下，砂井地基的固结曲线.可见当re逐渐增大时，最终的固结度逐渐减小.当re分别为0.40，0.45，0.50，0.55，0.60m时，最终固结度分别为91%，89%，87%，85%，83%.

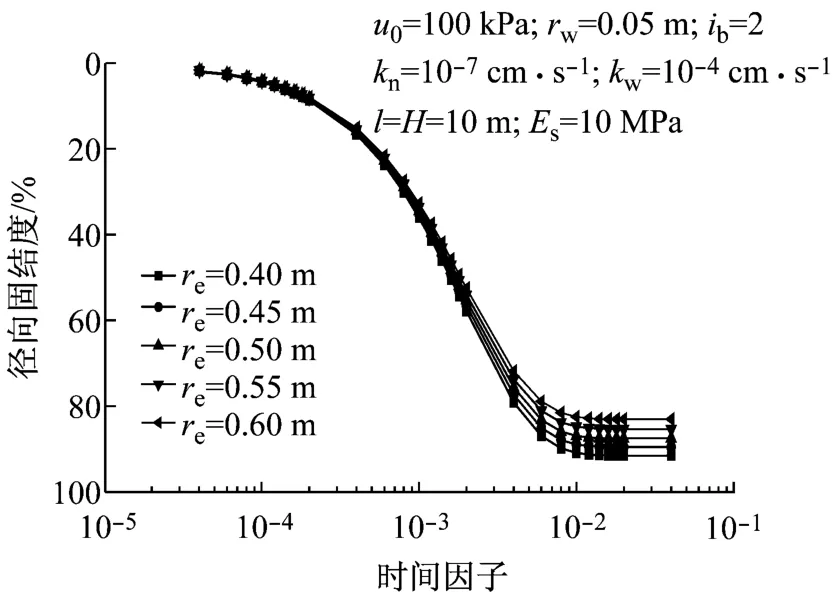
图4 影响区半径对固结度的影响Fig.4 Effect of influence zone radii on consolidation rate

图5 初始孔压对固结度的影响Fig.5 Influence of initial pore water pressure on consolidation rate

图5为不同的初始孔压下，砂井地基的固结曲线.可见当u0逐渐增大时，最终的固结度也逐渐增大.因为固结压力越大，在土体中产生的水力梯度越大，这有利于渗流的发生，使得孔压消散更为充分.但是，由图5可以发现，u0每增加20kPa时，对最终固结度的影响程度是不一样的.当u0从40kPa增加到100kPa时，最终的固结度从69%增加到87%，但是，若再继续增加u0则对最终的固结度影响不大.可以认为在本算例中，当u0达到100kPa后，最终的固结度对u0的灵敏度降低.

4 结论

（1）本文将考虑起始水力梯度的非达西渗流模型引入沙井地基固结理论，建立相应的控制方程，并通过详细的推导，给出了便于应用的显示解答.该解答可以退化为达西渗流模型的固结理论解.

（2）研究了考虑起始水力梯度时砂井地基的固结性状.结果表明，由于起始水力梯度的存在，应力固结度最终将稳定在一个小于100%的数值上，最终的固结度随着起始水力梯度增大而减小.

（3）考虑起始水力梯度存在时，影响区半径和初始孔压也会对砂井地基的固结性状产生影响.re越大，最终达到的应力固结度越小；u0越大，最终达到的应力固结度越大.但是需要注意的是，当u0增大到某一个值之后，若再继续增加u0则对最终的固结度影响不大.在本文算例中u0增大到100kPa之后，最终固结度对u0的灵敏度降低.

［1］ Barron R A.Consolidation of fine grained soils by drains wells［J］.Transactions of ASCE，1948，718.

［2］ Hansbo S，Jamiolkowski M，Kok L.Consolidation by vertical drains［J］.Geotechnique，1981，31（1）：45.

［3］ 谢康和，曾国熙.等应变条件下的砂井地基固结解析解理论［J］.岩土工程学报，1989，21（2）：3.XIE Kanghe，ZENG Guoxi.Consolidation theories for drain wells under equal strain condition［J］.Chinese Journal of Geotechnical Engineering，1989，21（2）：3.

［4］ 齐添，谢康和，胡安峰，等.萧山黏土非达西渗流性状的实验研究［J］.浙江大学学报：工学版，2007，41（6）：1023.QI Tian，XIE Kanghe，HU Anfeng，et al.Laboratorial study on non－Darcy seepage in Xiaoshan clay［J］.Journal of Zhejiang University：Engineering Science，2007，41（6）：1023.

［5］ Hansbo S.Consolidation equation valid for Darcy and non－Darcy flow［J］.Geotechnique，2001，51（1）：51.

［6］ 刘忠玉，刘忠广，马崇武.考虑起始水力梯度时饱和黏土的一维固结［J］.郑州大学学报：工学版，2006，27（3）：21.LIU Zhongyu，LIU Zhongguang，MA Chongwu.One－dimensional consolidation of saturated clays considering initial hydraulic gradient［J］.Journal of Zhengzhou University：Engineering Science，2006，27（3）：21.

［7］ 刘忠玉，孙丽云，乐金朝，等.基于非Darcy渗流的饱和黏土一维固结理论［J］.岩石力学与工程学报，2009，28（5）：973.LIU Zhongyu，SUN Liyun， YUE Jinchao，et al.Onedimensional consolidation theory of saturated clay based on non－Darcy flow［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（5）：973.

［8］ 周琦，邓志勇，王友元，等.起始水力梯度对真空预压下砂井地基固结过程的影响［J］.土木建筑与环境工程，2010，32（2）：46.ZHOU Qi，DENG Zhiyong，WANG Youyuan，et al.Effect of initial hydraulic gradient on consolidation of sand—drained ground improved by vacuum preloading［J］.Journal of Civil，Architectural ＆Environmental Engineering，2010，32（2）：46.

［9］ 卢萌盟，谢康和，王坤.考虑桩体内径向渗流的复合地基固结解［J］.固体力学学报，2009，30（2）：155.LU Mengmeng，XIE Kanghe，WANG Kun.Analytical solutions for the consolidation of a compound foundation with consideration on the radial flow within the column［J］.Chinese Journal of Solid Mechanics，2009，30（2）：155.

［10］ 中交天津港湾工程研究院有限公司.JTS 147－1—2010 港口工程地基规范［S］.北京：人民交通出版社，2010.CCCC Tianjin Port Engineering Institute，Co.Ltd..JTS 147－1—2010 Standard of foundations in port engineering［S］.Beijing：China Communications Press，2010.

［11］ Hansbo S.Consolidation equation valid for Darcy and non－Darcy flow［J］.Geotechnique，2001，51（1）：51.

［12］ Hansbo S.Aspects of vertical drain design：Darcy and non－Darcy flow［J］.Geotechnique，1997，5（47）：983.