基于意向偏好调查的需求组合模型参数标定方法

杨 超，蔡意田，何树林

（1.同济大学 道路与交通工程教育部重点实验室，上海201804；2.同济大学 建筑设计研究院（集团）有限公司，上海200092）

交通需求分析是交通规划中的基本定量分析手段，其计算精度直接影响城市交通规划的合理性.在目前的实践中，“四阶段”模型［1］是应用最为广泛的交通需求分析方法.但是，由于“四阶段”模型对出行者行为的描述是不一致的［2］，导致各个阶段中出行时间和拥挤效应的不一致性.近年来，非集计模型被逐步引入交通预测领域，并不断出现新的应用成果，为解决“四阶段”模型效用不一致问题提供了新的思路，特别是巢式罗吉特（Nested Logit，NL）非集计模型的提出，为统一出行行为各个阶段的效用提供了有力的工具.

作为非集计模型与交通需求分析相结合的产物——交通需求组合模型，将不同阶段影响个体出行决策的因素纳入同一个模型之中，不但体现了出行行为的整体性，而且更能够体现各种因素对于整个出行行为的影响，以及各个出行决策阶段的相互作用关系，理论上具有集计模型无可比拟的优势.近年来，组合模型理论在世界范围内得到一定推广，各国的交通模型研究者在不同的方向取得众多的研究成果［3－6］.但是目前交通需求组合模型的研究主要针对模型的构建和算法，对于模型参数的标定方法研究不多.因此在实际的交通需求预测中，交通需求组合模型的应用缺乏理论支撑.

为进行模型参数标定，通常需要开展调查.常用的调查 包 括RP（revealed preference）［7］调 查 和SP（stated preference）［8］调查.而Train and Wilson提出SP－off－RP的调查方法［9］既可以避免传统RP 调查设计范围小、只能针对已有行为调查的弱点，又利用SP调查的众多优点提高数据采集效率，扩大调查设计范围，实现了SP 调查与RP 调查的“优势互补”［10］.

本文提出利用改进的SP－off－RP 方法［10］获得的SP／RP数据进行交通需求组合模型参数估计，以提升需求预测模型的精确度，使得理论模型能够应用于交通需求预测实践.

1 交通需求组合模型

1.1 模型结构

交通需求组合模型将出行者看作出行的消费者，其出行选择与出行效用和预算有关［2］.在交通需求组合模型理论中，出行者的选择行为假定被划分成四个阶段，四个阶段具有逻辑上的先后顺序关系，后一阶段出行者的选择概率是一个基于前一次选择行为结果的条件概率.具体而言，需求组合模型中出行者出行选择行为分为4个层次，如图1所示.交通需求组合模型解的存在性和唯一性已经被证明［2］，该问题的求解可使用部分线性算法与二次插值法［11－12］等.

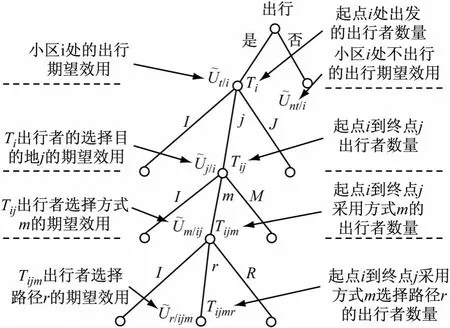
图1 交通需求组合模型中分层选择结构Fig.1 Hierarchical choice structure of combined travel demand model

1.2 目的地－方式选择组合模型

基于上述交通需求组合模型，构建只考虑目的地和出行方式选择的组合模型，用于说明利用调查SP／RP数据进行模型标定的方法.模型结构如图2所示.

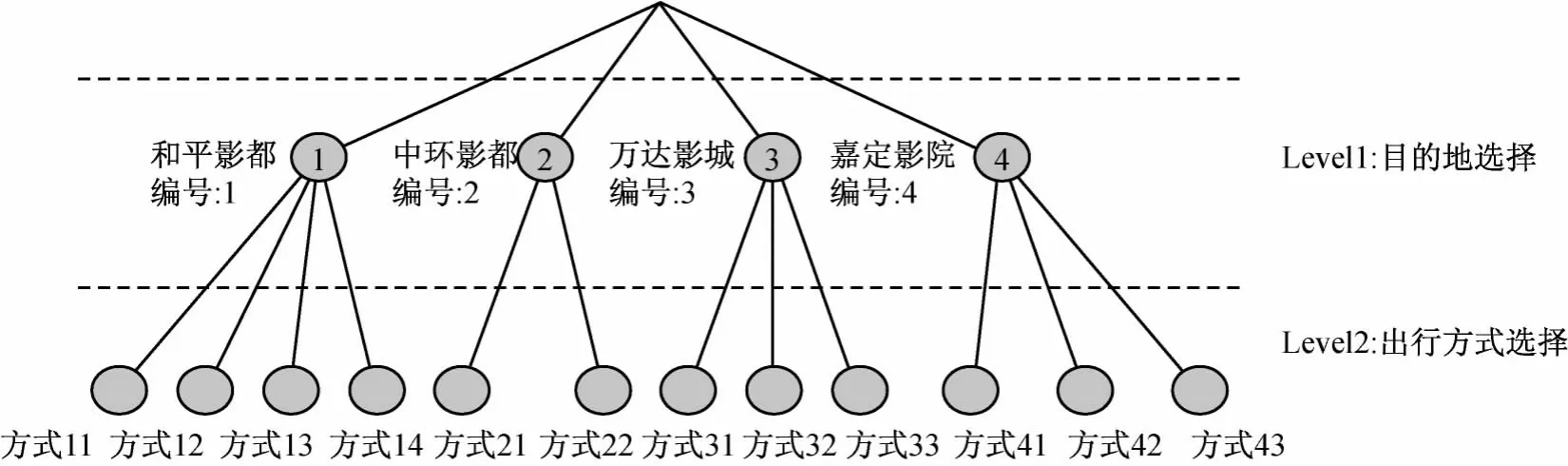
图2 目的地及方式选择组合模型结构Fig.2 Structure of combined destination and mode choice model

基于上述的模型结构，可以定义上下两层节点的效用函数.上层节点所代表目的地j选择效用函数为

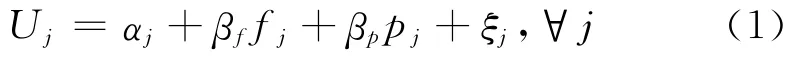
式中：Uj为目的地选择行为效用值；fj为目的地j费用变量；pj为目的地j消费品变量；ξj为随机项；αj，βf，βp是待估参数.由于上层节点构成了一个巢，因此巢系数为1，在效用函数中不体现.

下层节点由从属于各个目的地节点的出行方式构成，下层节点效用函数中只采用出行车内时间与出行费用作为效用函数自变量，效用函数为

式中：Ujm为第j个目的地第m种方式的选择效用；cjm为该节点所代表的出行方式的出行费用变量；t′jm为出行方式的车内时间变量；ξjm为随机项；βj，αjm，βc，βh是待估参数.

可以得到组合模型的联合概率公式为

式中：Pjm是选择目的地j方式m的概率为下层节点选择总体效用的期望值，其计算公式为

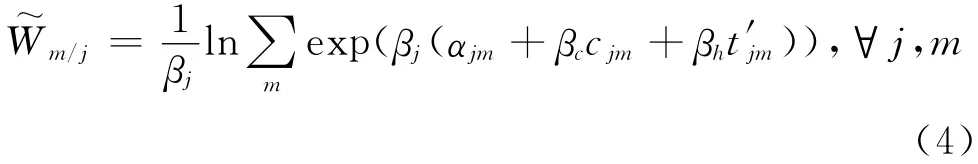
2 目的地与方式选择组合模型参数标定方法

完整的交通需求组合模型包括了出行决策的四个阶段：是否出行、目的地选择、交通方式选择和出行路径选择（见图1）.因为交通需求组合模型至少包括两个以上的选择阶段，即NL（Nested Logit）模型包含至少两层以上，所以标定模型参数比较适合采用逐层估计的极大似然法.下文将从单层（应用于NL模型各层参数估计）极大似然估计算法开始，介绍在组合模型中（以两层组合模型为例），如何实现逐层参数估计.假定一个出行者n，选择从出发点i到目的地j，其选择概率如下：

假定已经获得了一组出行者目的地选择结果样本，总数为N，其编号为1，2，3，…，n，…，N.定义一个贝努利指标δnj，如果出行者n选择j作为出行目的地，则δnj＝1，反之δnj＝0.样本中第n个出行者选择j作为目的地的概率为

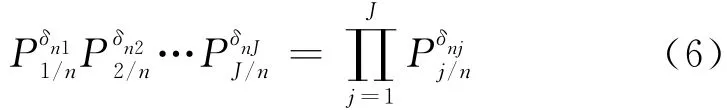
根据极大似然法的原理，令似然函数为

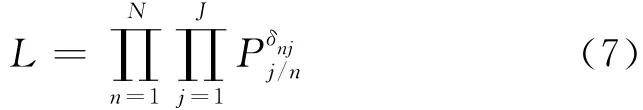
对似然函数取对数，原函数的特性仍保持不变

当式（8）取最大值时，参数αj，βf，βp的值即为所需的估计值.因此对式（8）中αj，βf，βp分别求偏导数，令偏导数为0，可得方程组

求解方程组（9），可求得参数αj，βf，βp.

通过上述单层Logit模型利用极大似然法进行参数估计的过程，能够说明交通需求组合模型中每一层结构中各巢（实质为附带巢系数的多项罗吉特模型（MNL））内节点效用函数待估参数的估计过程.但是多层的NL 模型与MNL 模型相比，由于分层结构的存在，使得参数估计的计算在MNL 模型参数估计的计算基础上增加了各层之间的递进估计的关系（表现为巢系数的存在）.

3 改进的SP－off－RP调查

在进行非集计模型参数标定时，通常使用RP［7］或SP［8］调查获得数据，并利用极大似然法进行参数估计.但RP或SP调查有各自的优缺点.近年来，研究者们一直尝试“联合”使用RP数据与SP数据［9］.

3.1 SP－off－RP方法及改进

Train和Wilson［9］提出了SP－off－RP的调查与数据联合利用原则，并通过蒙特卡罗法印证了该原则能够比较有效对SP／RP 数据起到联合利用的作用，实现两种数据的优势互补，从而提高数据的质量，提升所建立非集计模型的精确度.但是Train和Wilson的方法存在一定的缺陷，即只记录两次受访者的反应（初始选择与改变选择），无法体现不同因素的不同水平对于受访者考虑权衡的过程.同时，一个受访者只采集两个数据，数据采集效率比较低.更重要的是，由于该方法以受访者反应作为下一步调查的基础，受访者与调查的互动成为必然，而传统调查法无法实现这一过程，降低了该方法的实用性.由于受上述限制，Train等人只能从理论上论证方法的合理性，无法以实践的调查检验理论，严重影响了SP－off－RP调查的应用.

本次研究对SP－off－RP 方法进行部分修正［10］并设计基于网络的调查工具，以实现该方法的实际应用.改进的思路是：在原方法的基础上细化SP情景生成规则，改进数据采集规则，改变调查终止条件.用户在所有SP调查情景中的选择结果均被作为数据联合结果反馈到研究者的数据记录中，如图3所示.

3.2 基于互联网的个体行为调查设计及数据采集平台

由于改进后的SP－off－RP方法强化了调查问卷与受访者之间的互动，本次研究基于互联网技术开发“个体行为调查设计及数据采集平台”，该软件集成了在线调查问卷设计与发布功能以及受访者在线参与调查功能.通过设置动态问卷设计功能为出行行为等大型社会调查提供编辑SP－off－RP互动式问卷功能.该软件实现了根据受访者在某一调查情景中的表现（选择选项、选择理由）生成新的调查情景的机制.研究者通过互动式问题设计模块的各种设置，可以为受访者提供动态的调查体验.具体流程如图4所示.

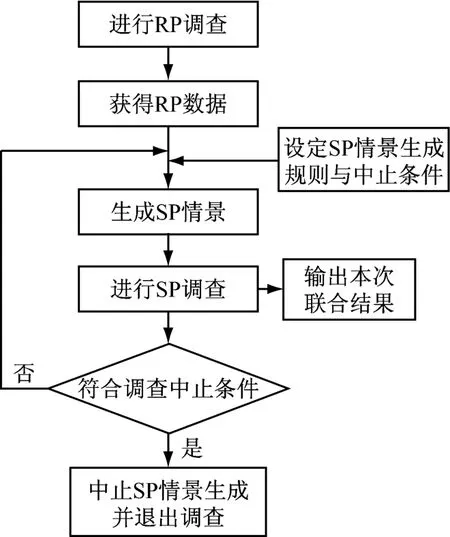
图3 改进后SP－off－RP方法逻辑示意图Fig.3 The improved SP－off－RP logic diagram

4 算例

图4 互动式模块功能实现流程图Fig.4 Interactive function flow chart

本文以上海市同济大学嘉定校区学生观看3D影片《阿凡达》的出行行为作为分析对象，利用“个体行为调查设计及数据采集平台”设计基于互联网的调查问卷.考虑从嘉定校区为出发点到4个公交可到达的、具有3D 放映能力的电影院为目的地.由于学生的主要出行方式为公交，且从嘉定校区出发可选择的交通方式有限，因此将方式选择和路径选择合并为一个环节（此处定义为交通方式）加以考虑.嘉定校区到4个影院观影出行示意图如图5所示.

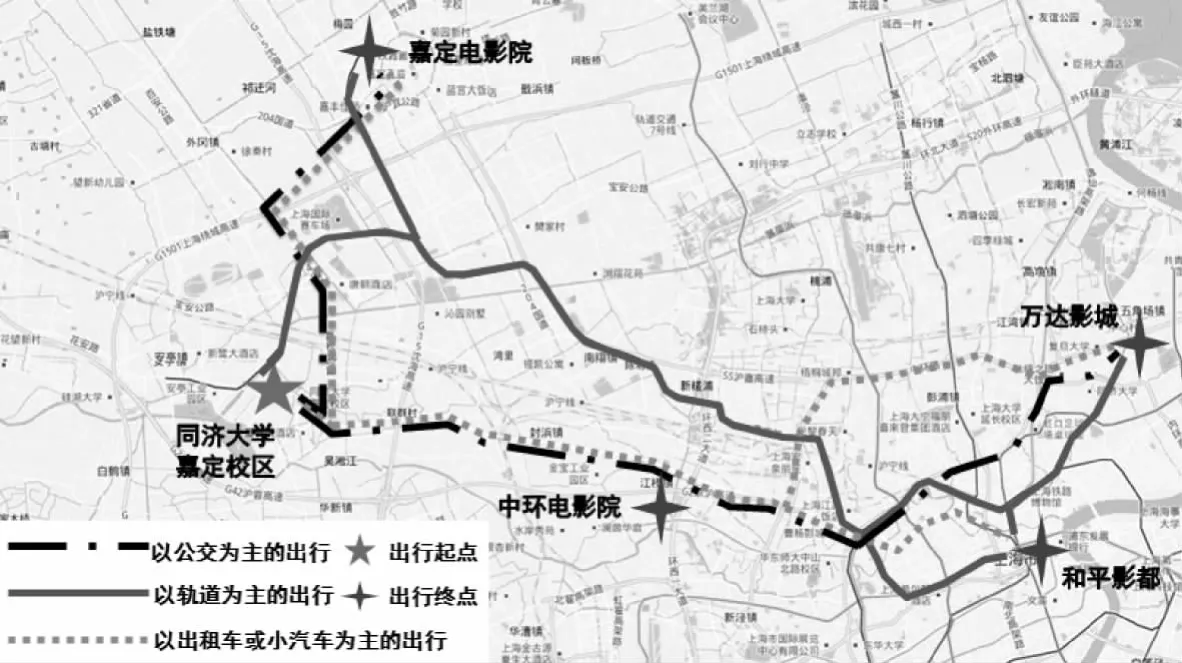
图5 同济大学嘉定校区观影出行路径示意图Fig.5 Routes for film－watching in Jiading campus of Tongji University

4.1 数据获取与处理

本次调查于2010年3 月中上旬完成背景资料收集、小范围预调查以及实地考察等环节，2010年3月下旬至4月初完成网上问卷设计与问卷调试，4月9日完成随机抽样生成受访者名单并完成了调查邀请的发布，5月21日至5月28日为网络调查开放时间，受访者可以根据邀请中提供的密码和网址访问该网站并接受调查.一共采集到问卷157份，有效数据样本118份.

由于在本次调查中，出行者首先考虑的是目的地对其产生的吸引力，表现为这4个电影院提供服务的差异对于出行者选择行为的影响.4个目的地的属性如表1所示.

表1 出行目的地属性列表Tab.1 Property of destinations

本次实例验证中的目标模型是体现交通需求组合模型概念的两层NL 模型（组合了出行目的地选择行为与出行方式选择行为，基本结构如图2所示.图中目的地编号与表1对应.表2中给出到达各目的地的交通方式编号及相应属性.

表2 不同目的地下属出行方式属性列表Tab.2 Property of the travel modes of different destinations

表2中深色背景的3种交通方式是从嘉定校区出行观影行为发生时在现实环境中尚不存在的交通方式，轨道交通11号线支线段在2011年投入使用，因此可以将包括轨道交通11号线的出行方式作为虚拟的元素加入到SP调查设计中.

4.2 模型参数估计与结果分析

根据模型结构与各节点效用函数构成，按照第2节中介绍的逐层估计法，从底层各个巢的下属节点开始，逐巢逐层对模型进行参数估计.利用NLogit4.0［13］软件，将有效调查数据代入模型中对各待估参数进行估计，结果如表3所示.

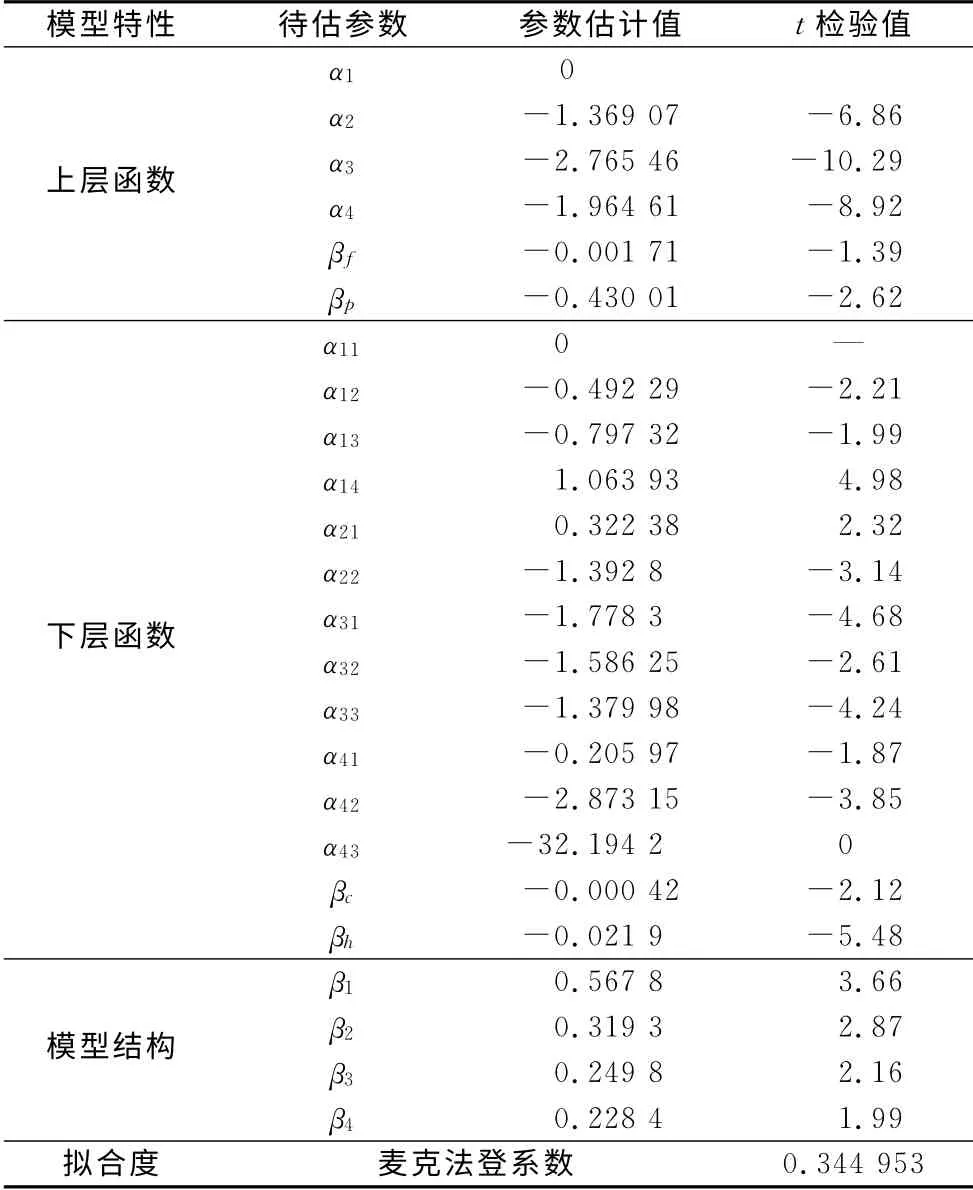
表3 目标模型参数估计结果Tab.3 Results of the parameter estimation

由表3可以看到，22个待估参数中，大部分（19个）参数估计值的t检验值均大于1.96，即能保证具有95%的置信度，在3个t检验值小于1.96的参数中，有两个（βf，α41）的t检验值大于1，表现出对选择效用具有显著性影响，只有一个参数（α43）的t检验值近似为0.同时麦克法登系数为0.344 953（＞0.2），说明拟合精度较高.根据上述参数估计结果，可以计算出目标模型上下层效用函数值，如表4所示.

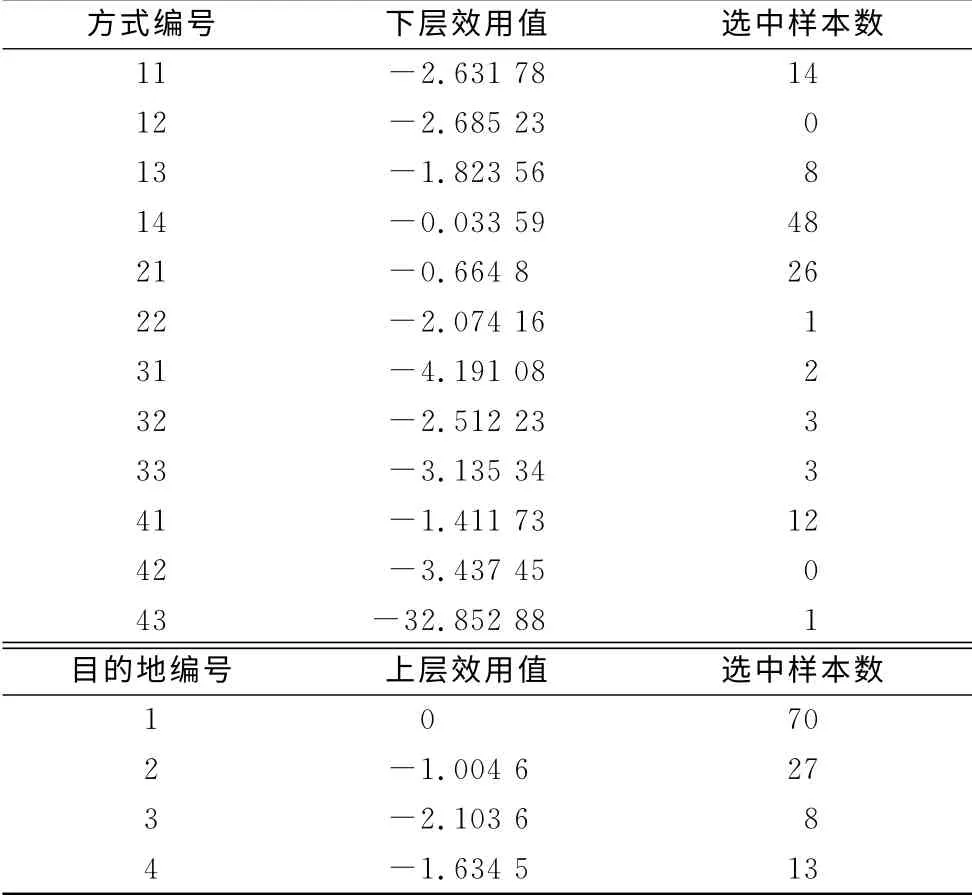
表4 目标模型上下层效用函数值Tab.4 Utility function value of objective model

从表4可知，目的地选择行为效用（上层效用）越大，被受访者选中的频数越高，这符合理性选择行为的逻辑.同时，表4中大多数结果显示，在同一个目的地下，出行方式选择效用（下层效用）越大，则被选中的频数越高，这也符合理性选择行为的逻辑.唯一的例外是方式43，其效用值非常小，但是仍旧有1个人选择了这种出行方式，与效用值大其10倍的方式42被选中的频数却反而为0，这不符合逻辑，这也可以一定程度解释，为什么方式43的效用函数固定项参数估计值的t检验值趋近于0的原因.因此用这样的选择结果估计模型参数会导致误差.

5 结论

本文介绍了交通需求组合模型，提出利用改进的SP－off－RP调查进行模型参数标定，开发了“基于互联网的个体行为调查设计及数据采集平台”用于调查数据采集.结合上海市同济大学嘉定校区学生观影调查的SP／RP数据，建立了目的地及方式选择组合模型，并对模型进行了标定与验证.验证结果表明，通过SP／RP数据标定的参数估计值具有较高的估计精确度，同时由这些估计值所构建的目标函数，能够很好地反映客观现实，具有较高的可信度.

［1］ Ortuzar J D，Willumsen L D.Modeling transport［M］.3rd ed.New York：John Wiley ＆Sons Inc.，2001.

［2］ Oppenheim N.Urban travel demand modeling［M］.New York：John Wiley ＆Sons Inc.，1995.

［3］ Zhou Z，Chen A，Wong S C.Alternative formulations of a combined trip generation，trip distribution，modal split，and trip assignment model ［J］.European Journal of Operational Research，2009，198：129.

［4］ Huang H，Lam W H K.A stochastic model for combined activity／destination／route choice problems ［J］.Annals of Operations Research，2005，135：111.

［5］ Ho H W，Wong S C，Loo B P Y.Combined distribution and assignment model for a continuum traffic equilibrium problem with multiple user classes［J］.Transportation Research Part B，2006，40：633.

［6］ Boyce D，Bar－Gera H.Validation of multiclass urban travel forecasting models combining origin destination mode and route choice［J］.Journal of Regional Science，2003，43（3）：517.

［7］ Samuelson P.A note on the pure theory of consumers behaviour［J］.Economica，1938，5（17）：61.

［8］ Thurstone L L.The indifference function［J］.Journal of Social Psychology，1931，2（2）：139.

［9］ Train K，Wilson W E.Monte Carlo analysis of SP－off－RP data［J］.Journal of Choice Modelling，2009，2（1）：101.

［10］ 何树林，杨超.改进的SP－off－RP调查方法［C］／／中国大城市交通规划研讨会论文集.苏州：中国城市规划学会城市交通规划学术委员会，2010：1020－1029.HE Shulin，YANG Chao.Improved SP－off－RP survey method［C］／／Proceeding of China Urban Transportation Planning Forum.Suzhou：Committee of Urban Transport Planning in Chinese Urban Planning Society，2010：1020－1029.

［11］ 蒲琪，杨超，涂颖菲.基于二次插值法的交通需求组合模型算法［J］.同济大学学报：自然科学版，2009，37（12）：1615.PU Qi，YANG Chao，TU Yingfei.A quadratic interpolation method－based algorithm for a combined travel demand model［J］.Journal of Tongji University：Natural Science，2009，37（12）：1615.

［12］ Yang C，Chen A，Xu X D.Improved partial linearization algorithm for solving the combined travel－destination－mode－route choice problem ［J］.Journal of Urban Planning and Development.DOI：10.1061／（ASCE）UP.1943－5444.0000130，online 2012／5／15.

［13］ NLOGIT version 4.0：reference guide ［M］.Plainview：Econometric Software，2007.