真空联合堆载预压下基于指数形式渗流的砂井地基非线性固结解
2021-03-02江文豪詹良通
江文豪,詹良通
(浙江大学岩土工程研究所,杭州310058)
真空预压法是工程上常用的软土地基加固方法[1],真空预压法通常与砂井(目前多为塑料排水板)结合使用。在工程设计中,常采用砂井地基固结理论来研究真空预压下土体的固结过程[2-6]。董志良[2]建立了真空预压下砂井地基的固结方程,并得到了砂井地基径向固结的解析解。Indraratna等[3]假定砂井内真空负压沿竖向深度呈线性衰减分布,求得了整个地基的平均固结度公式。周琦等[4]假定砂井下边界的真空负压随时间变化,获得了真空预压下砂井地基的Hansbo固结解。韩文君等[5]基于双对数压缩模型,求得了真空预压下砂井地基的非线性固结解。张玉国等[6]考虑了径向渗透系数的变化,对真空预压下砂井地基的固结问题展开了分析。
为提高砂井地基真空预压法的加固效果,工程上常采用真空联合堆载预压法进行地基加固[7-8]。Rujikiatkamjorn 等[7]考虑了砂井地基径向和竖向的组合渗流,研究了真空联合堆载预压下砂井地基的固结问题。郭彪等[8]通过考虑堆载所引起的附加应力随时间和深度变化,求得了真空联合堆载预压下砂井地基固结的一个普遍解析解。胡亚元[9]考虑到砂井地基的实际排水边界为半透水边界,获得了真空联合堆载预压下砂井地基的固结解。郭霄等[10]通过假定孔隙比和有效应力、渗透系数之间为半对数线性关系,推导得到了适用于真空联合堆载预压法的通用解析解。
在上述砂井地基的固结理论中,其渗流定律均基于Darcy 定律。然而,室内和现场试验表明,Darcy 定律对渗透性较弱的软黏土却不一定适用[11-16]。齐添等[13]和孙丽云等[14]对软黏土展开渗透试验指出,土中的渗流规律采用指数形式渗流规律进行拟合的效果更好。Slepicka[16]提出了指数形式的渗流定律,即:

式中,v为渗流速度;k为土体的渗透系数;i为水力坡降;m为渗流指数。
对于指数形式渗流定律下砂井地基的固结问题,Hansbo[17-18]考虑到土体的渗流规律为指数形式渗流定律,求解得到了砂井地基固结的一个解析解。Kianfar 等[19]通过考虑真空预压和指数形式渗流定律,推导得到了砂井地基的径向固结解。刘忠玉等[20]基于指数形式渗流定律,采用数值方法对理想砂井地基的性状进行了固结分析。Indraratna等[21]通过考虑土体的大变形固结特性、真空预压和指数形式渗流定律,研究了砂井地基的大变形固结问题。然而,上述研究中均未考虑真空负压向下传递过程存在的损失,且对于真空联合堆载预压下,砂井地基的非线性固结问题,目前相关研究较少。
基于此,本文基于Slepicka[16]所提出的指数形式渗流定律,同时考虑土体的非线性固结特性和真空负压沿深度呈线性衰减的特性,求解得到了真空联合堆载预压下砂井地基的非线性固结解。通过将本文解析解答与已有的解析解进行比较分析,对本文解答的正确性进行了验证。基于本文解答,对影响砂井地基固结性状的一些因素展开了分析。
1 砂井地基的计算模型
1.1 计算简图
以单井为研究对象,考虑真空联合堆载预压下砂井地基非线性固结的计算简图如图1。
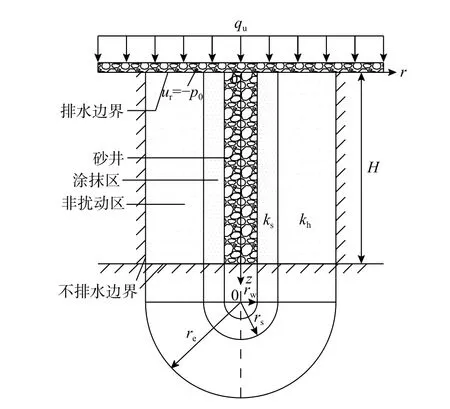
图1 砂井地基的计算简图Fig.1 Calculation diagram of sand-drained ground
这里假定砂井地基的顶面为排水边界,底面为不排水边界。图1中:砂井地基的厚度为H;r、z分别为径向坐标和竖向坐标;qu为上表面作用的瞬时均布荷载;p0为作用于地基表面的真空负压;rw、rs、re分别为砂井半径、涂抹区半径及砂井的影响区半径;ks、kh分别为涂抹区和非扰动区土体的径向渗透系数。
1.2 基本假定
在本文的推导过程中,做如下基本假定:
①等应变条件成立[10],即砂井影响区范围内同一水平面上各点的竖向变形是相同的;
②考虑土体的非线性固结特性,土体的径向渗透系数kr、孔隙比e和任一深度处径向范围内的平均有效应力 σ¯′存在以下关系:
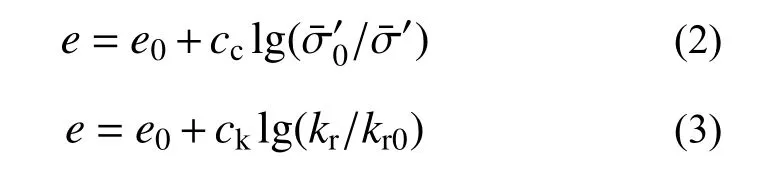

⑥在任一深度处从土体流入砂井的水量等于砂井中向上水流的增量。
1.3 控制方程及其边界条件
式中,mv为体积压缩系数;u¯r为砂井影响区内任意深度处的平均孔压;u¯r的表达式如下:


式中, Θ的表达式与渗流指数m有关。
当m=1时(Darcy 定律成立), Θ的表达式如下:

2 计算模型的求解


在任意时刻,砂井地基的沉降量St为:

3 计算模型的验证
从式(28)和式(29)中平均孔压u¯r的表达式可以看出,渗流指数m=1时(Darcy 定律成立)解答的表达式与m≠1时的表达式完全不同。因此,以下将分别对m=1时和m≠1时的解答进行验证。
3.1 m=1时的解答验证
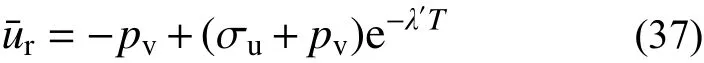
对于Darcy 定律下砂井地基的非线性固结问题,郭霄等[10]通过考虑外荷载随时间的变化及真空负压随深度递减,求得了不同工况下砂井地基的非线性固结解。在瞬时荷载下,郭霄等[10]求解得到平均孔压u¯r的表达式如下:式中,pv为沿砂井深度呈线性衰减的真空负压;σu为瞬时堆载引起的土中附加应力;λ′为与深度z有关的系数,T为与时间t有关的系数。将式(28)与式(37)进行比较分析可知,m=1时本文解答的表达式与郭霄等[10]解答的表达式形式上完全一致,系数的物理意义也基本相同,这验证了m=1时本文解答的正确性。
3.2 m ≠1时的解答验证

进一步,若不考虑固结过程中土体的非线性特性,则方程的解答可以转化为:

Hansbo[18]及Kianfar 等[19]均求解得到了小应变线性固结下基于指数形式渗流的砂井地基固结解。通过比较平均孔压u¯r的表达式可知,式(39)中u¯r的表达式与Kianfar 等[19]求解真空联合堆载预压下u¯r的表达式形式上一致,系数的物理意义基本相同。通过比较平均固结度的表达式可知,式(40)中平均固结度的表达式与Hansbo[18]求解堆载下平均固结度的表达式形式上较为一致,系数的物理意义也基本相同。通过将m≠1时本文退化解与已有的解析解进行对比分析可知,本文解答与已有的解析解较为一致,这验证了m≠1时本文解答的正确性。
4 固结性状分析
Dubin 等[12]研究了软黏土中渗流指数m的范围,认为m=1.5时与试验结果较为符合。齐添等[13]利用GDS高级固结仪对萧山黏土的渗流规律展开试验研究,试验分析指出m处于0.71~0.76。孙丽云等[14]对河南某地饱和黏土的非达西渗透特性进行了研究,试验统计发现m处于1.42~1.82。可以看出,不同区域处饱和黏土的m的取值有较大差异,考虑到m的取值大多应与m=1时相接近,这里仅分析取m值处于0.8~1.2。
为研究指数形式渗流定律下砂井地基的非线性固结性状,取渗流指数m=1.1,砂井地基的计算参数以表1中的计算参数为基准,基于上述解析解答,对影响地基固结性状的一些因素展开分析,其中包括渗流指数m、负压传递系数kz、cc/ck值及外荷载qu。
图2给出了不同渗流指数m下砂井地基的平均孔压固结度曲线。从图2中可以看出,渗流指数m对砂井地基固结速率的影响十分显著,在固结初期,m越大,地基的固结速率越快;而在固结后期,m越大,地基的固结速率越慢。出现这一固结性状的原因可从式(1)中得到解释。在固结初期,土体的水力坡度较大(大于1),从式(1)可知,指数形式渗流定律下土体的渗流速度随着m的增大而增大;在固结后期,土体的水力坡度较小(小于1),从式(1)可知,指数形式渗流定律下土体的渗流速度随着m的增大而减小。

表 1砂井地基的计算参数Table1 Calculation parametersof the sand drainsfoundation
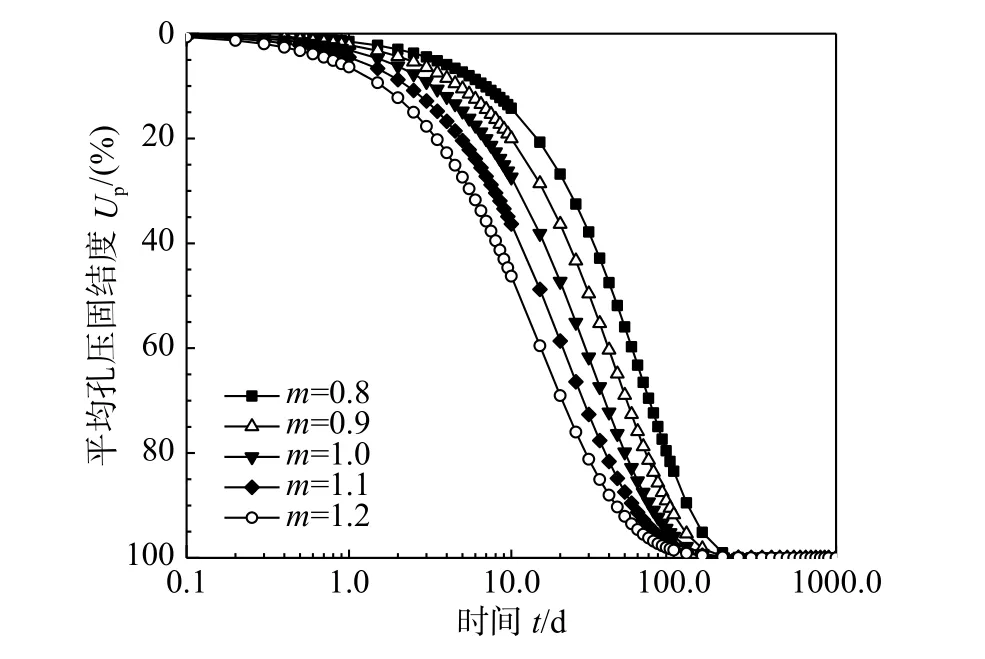
图2 渗流指数m对平均孔压固结度的影响Fig.2 The influence of flow index m on average pore pressure consolidation degree
图3给出了不同负压传递系数kz下砂井地基的平均固结度曲线。可以发现,kz的变化对砂井地基固结速率的影响较小,不同kz下砂井地基的平均固结度曲线几乎完全重合。此外,从图3中可以看出,固结过程中砂井地基的平均孔压固结度始终慢于平均沉降固结度,这主要是由于非线性压缩关系下,土体的压缩性随着有效应力的增大而减小。

图3 负压传递系数k z 对平均固结度的影响Fig.3 Theinfluence of negative pressuretransfer coefficient k z on average consolidation degree
图4所示为不同负压传递系数kz下砂井地基的沉降量曲线。可以看出,kz对砂井地基的沉降速率与沉降量有较大影响,土体的沉降速率与最终沉降量均随kz的减小而降低。综合图3和图4可知,尽管真空联合堆载预压下砂井的井阻效应对砂井地基固结速率的影响较小,但负压传递系数kz的减小会使得砂井地基的沉降速率和最终沉降量减小。
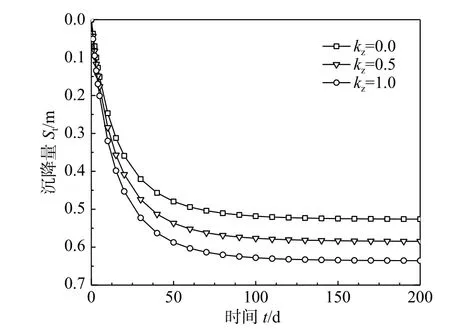
图4 负压传递系数k z 对沉降量的影响Fig.4 Theinfluence of negative pressure transfer coefficient k z on settlement
根据Berry 和Wilkinson[23]等研究,土体的cc/ck值范围大多介于0.5~2.0。这里给出了该cc/ck值范围内砂井地基的平均孔压固结度曲线,如图5。从图5可以发现,cc/ck值对砂井地基的固结速率有较大影响,cc/ck值越大,砂井地基的固结速率越慢,这与Darcy 定律下砂井地基的固结特性一致。该固结性状可直接从式(25)得到解释,cc/ck值越大,相同工况下系数λa越小,因而减慢了砂井地基的固结速率。
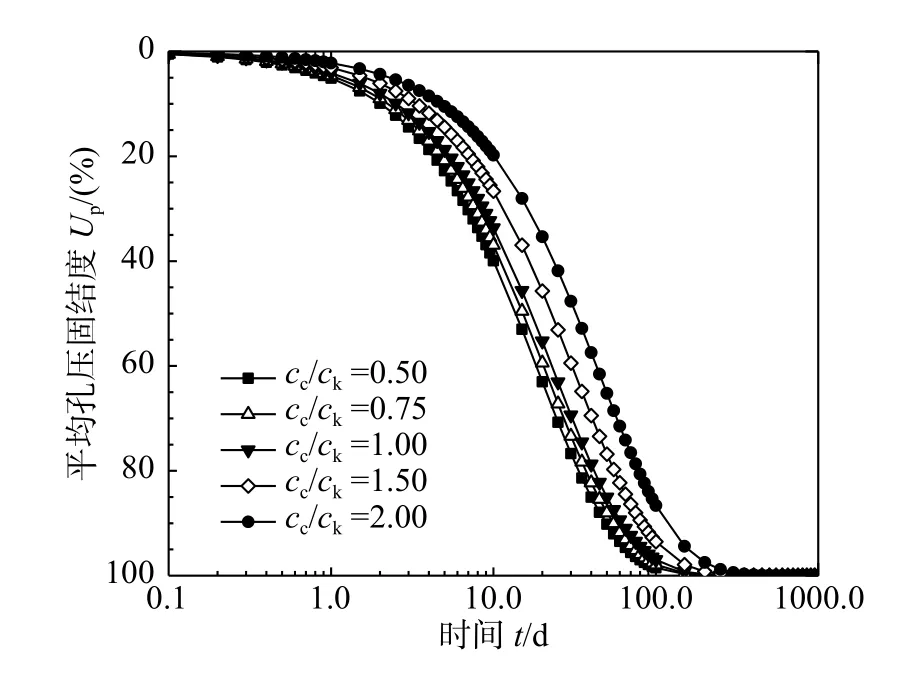
图5 c c/c k 值对平均孔压固结度的影响Fig.5 The influence of c c/c k values on average pore pressure consolidation degree
对于Darcy 定律下(m=1时)砂井地基的非线性固结问题,郭霄等[10]研究指出,当cc/ck<1时,外荷载越大,固结速率越快;当cc/ck=1时,固结速率不受外荷载大小的影响;当cc/ck>1时,外荷载越大,固结速率越小。然而,对于指数形式渗流定律下砂井地基的非线性固结特性,从式(29)可知,不同外荷载下地基固结速率的发展规律还受m的影响。因此,为研究指数形式渗流定律下外荷载qu对砂井地基的固结速率,假定cc/ck=1,不同外荷载qu下砂井地基的平均孔压固结度曲线如图6。
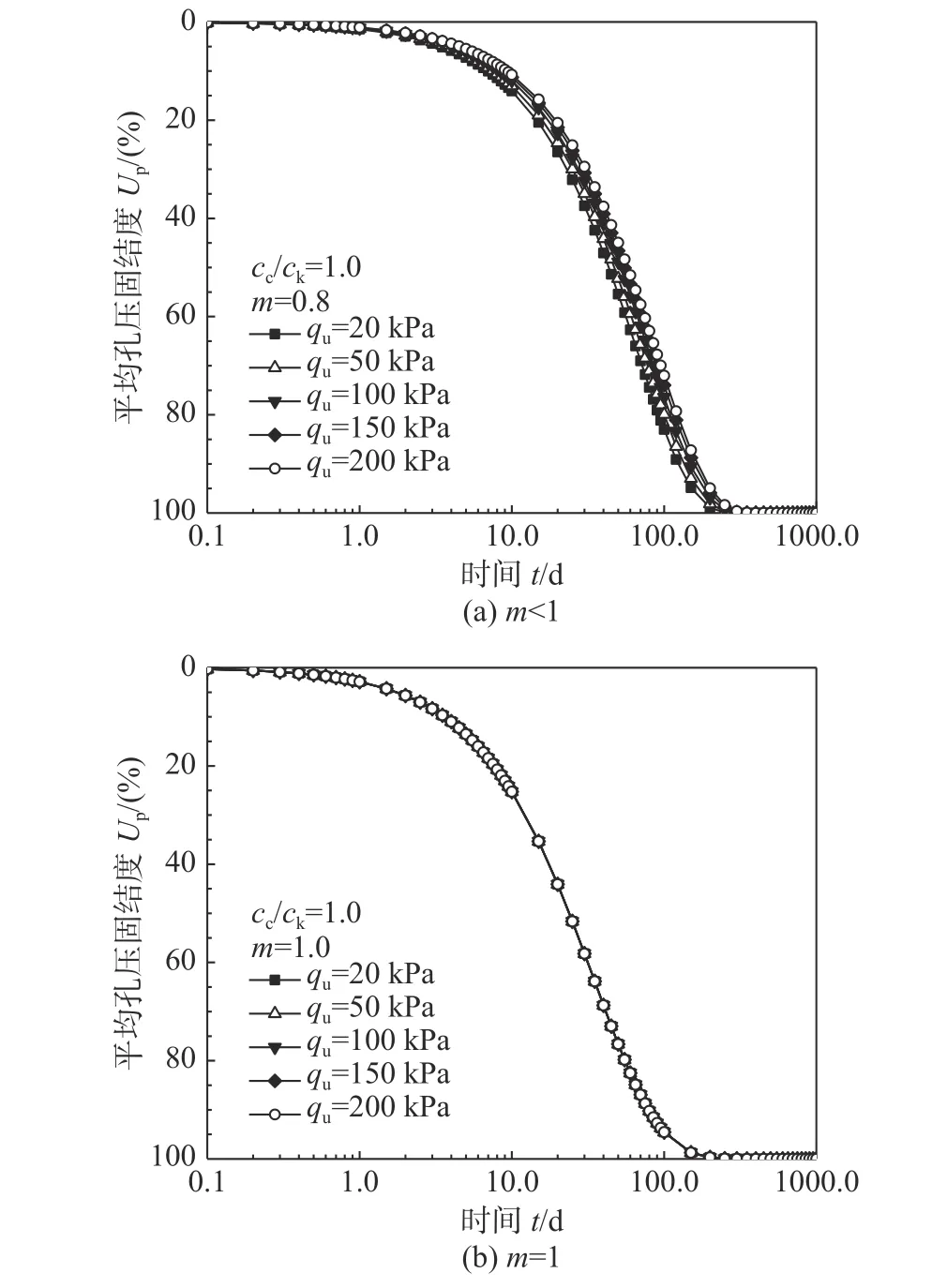
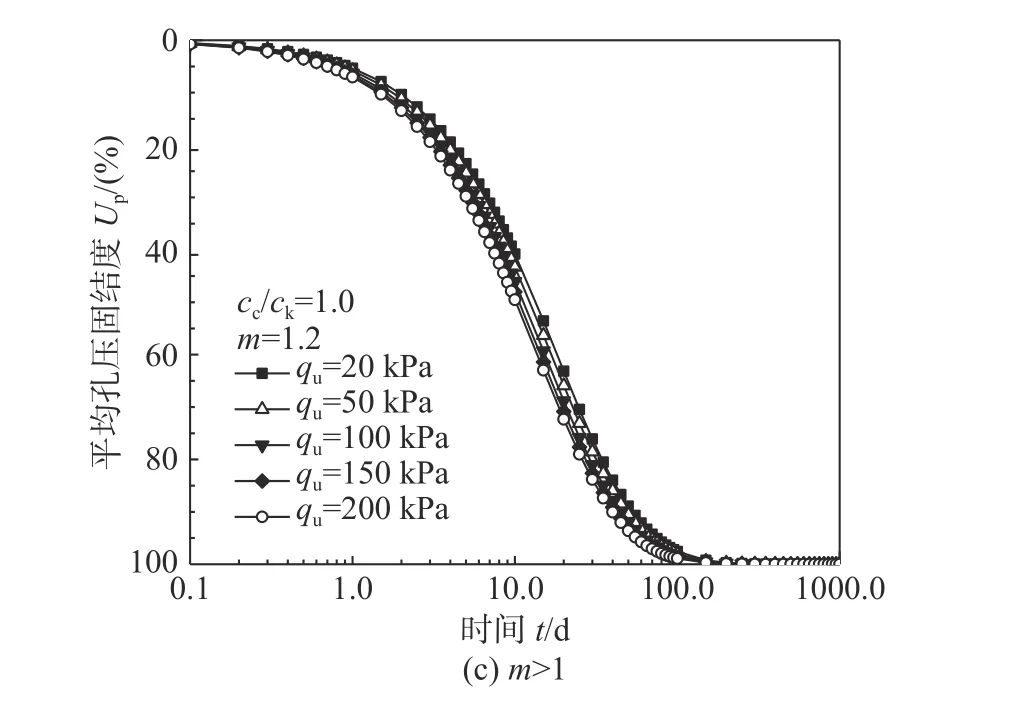
图6 外荷载q u 对平均孔压固结度的影响Fig.6 The influence of surcharge loadings on average pore pressure consolidation degree
从图6可以发现,不同外荷载qu下地基固结速率的发展规律受m的影响较大。当m<1时,砂井地基的固结速率随外荷载的增大而减小;当m=1时,外荷载的变化对砂井地基的固结速率无影响;当m>1时,砂井地基的固结速率随外荷载的增大而增大。这主要是由于外荷载越大,固结过程中土体的水力坡度i也越大。当m<1时,m越小,其渗流速度与达西流速的比值就越小,固结速率越慢;当m>1时,m越大,其渗流速度与达西流速的比值就越大,固结速率越快。
结合式(25)可知,指数形式渗流定律下,外荷载对砂井地基固结速率的影响规律受cc/ck值和渗流指数m的共同影响。在相同的工况下,当cc/ck>1且m<1时,外荷载越大,砂井地基的固结速率越小;当cc/ck=1且m=1时,不同外荷载下砂井地基的固结速率相同;当cc/ck<1且m>1时,外荷载越大,砂井地基的固结速率越大。
5 结论
本文基于指数形式渗流定律,考虑了土体的非线性固结特性和真空负压沿深度呈线性衰减的特性,对真空联合堆载预压下砂井地基的非线性固结问题进行了求解,推导得到了砂井地基的非线性固结解。通过将本文解析解答与已有的解析解展开比较分析,对本文解答的正确性进行了验证。根据解析解答,对砂井地基的固结性状展开了分析,并得到了如下结论:
(1)渗流指数m对砂井地基固结速率的影响十分显著,在固结初期,m越大,地基的固结速率越快;而在固结后期,m越大,地基的固结速率越慢。
(2)负压传递系数kz对砂井地基固结速率的影响较小,不同kz下砂井地基的平均固结度曲线几乎完全重合,但负压传递系数kz的减小会使得砂井地基的沉降速率和最终沉降量均减小。
(3)压缩指数与渗透指数的比值(cc/ck值)对砂井地基的固结速率有较大影响,cc/ck值越大,砂井地基的固结速率越慢,这与Darcy 定律下砂井地基的固结特性一致。
(4)在相同的工况下,当cc/ck>1且m<1 时,外荷载越大,砂井地基的固结速率越小;当cc/ck=1且m=1时,不同外荷载下砂井地基的固结速率相同;当cc/ck<1且m>1时,外荷载越大,砂井地基的固结速率越大。
