基于最小均方误差的认知雷达估计波形设计方法
2013-12-01张剑云王小平
曹 磊,张剑云,王小平,张 鑫
(解放军电子工程学院,安徽 合肥 230037)
0 引言
认知雷达(Cognitive Radar,CR)[1]是针对复杂电磁环境下目标探测提出来的一种新体制雷达,它与传统雷达的不同主要体现在以下三个方面:1)雷达通过不断地与环境的交互来实现对环境的学习并获取环境的相关知识以及目标的特性;2)发射机根据反馈信息和先验知识智能调整照射方式,以实现对环境可靠、有效和稳健地探测;3)雷达所处环境、发射机以及接收机三者组成一个动态、闭环反馈的雷达系统。因此,用一句话总结认知雷达的本质:通过与环境不断的交互而理解环境并适应环境的闭环雷达系统。
目前,关于认知雷达的研究主要集中在最优发射波形设计方面。大部分是针对目标为确定信道,且假设雷达已经获得了准确的目标冲激响应,进而根据特定的某种准则设计出最优检测[2-3]、识别[4-5]、跟踪[6]等波形。但许多目标的散射特性可能是随机分布的,且雷达刚开机时,往往并不具备目标的相关信息。由此可见,提出一种针对随机信道目标的最优估计波形设计方法是十分有意义的。
1 认知雷达波形设计和MMSE准则
1.1 认知雷达波形设计基础状况
图1所示为CR单次循环的离散信号模型。
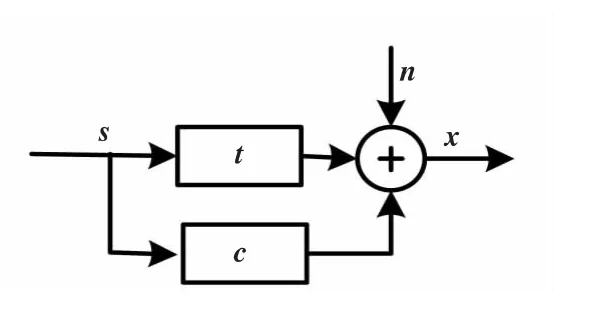
图1 信号模型Fig.1 The signal model
目标和杂波被建模为冲激响应为t∈CNt×1和c∈CNc×1的有限冲激响应(FIR)滤波器[2-3]。其中Nt=Nc。雷达接收回波可以表示为:
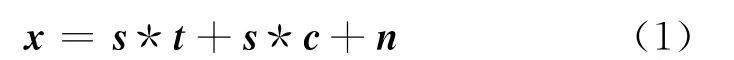
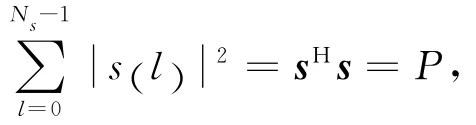
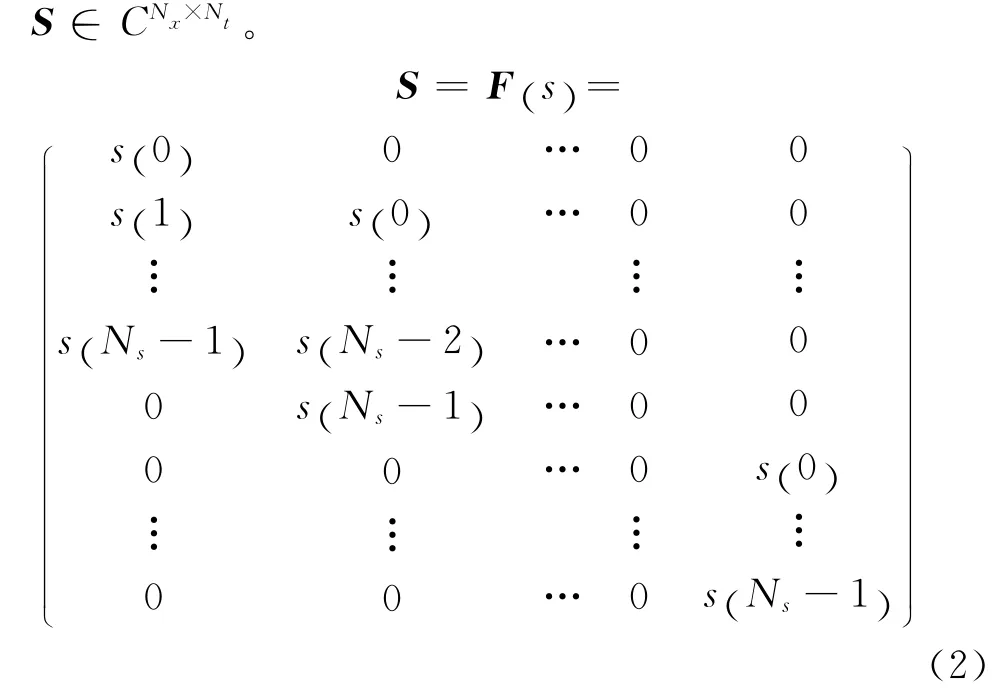
因此,式(1)可以表示为矩阵乘积形式:
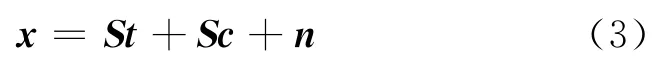
关于认知雷达波形设计,识别和检测方面的研究较多,大部分是假设信号模型中的目标冲激响应t是已知的,然后设计相应的最优波形。文献[4]假设系统已经获得关于目标冲激响应t的先验知识后,提出了一种基于遗传算法和最大滑动相关分类器的波形优化方法。该方法定义目标回波和同类模板之间的匹配系数与该目标回波和异类模板之间匹配系数的差为匹配距离,以最大化各类目标之间的匹配距离的最小值为优化准则,然后通过遗传算法进行求解,得到最优识别波形。文献[5]针对多个目标的识别问题,基于互信息准则,通过最大化接收到的信号与目标冲激响应线性加权和的互信息获得了针对多个目标识别的最优波形。而文献[2]中,则针对系统在未知的确定信道目标情况下,提出了首先通过对目标冲激响应进行t估计,然后根据估计得到的目标先验知识设计了最优检测波形。
1.2 最小均方误差(MMSE)准则
在寻找最佳估计量的时候,我们需要某些衡量标准,最常见的就是均方误差(MSE),它度量了估计值偏离真实值的平方偏差的统计平均值。
当估计子为高斯分布矢量x时,则估计子x和量测信息y联合分布的均值和协方差矩阵分别为:
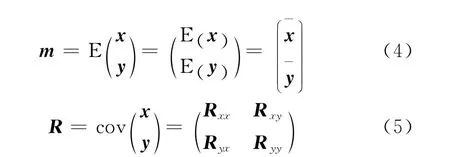
当R和Ryy非奇异时,那么在给定量测信息y,对估计误差的任意容许损失函数,参数x最小后验期望损失估计[7]公式为:
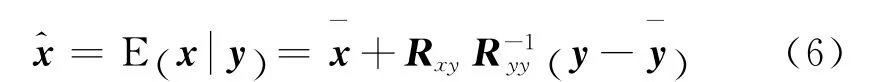
进一步得到估计子的 MSE[8-12]为:
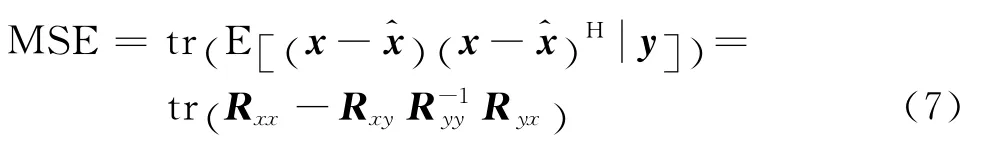
为了得到估计子的最优估计值,常常采用使MSE最小作为标准,即最小均方误差准则。
2 基于MMSE的波形优化方法
2.1 原理
本文考虑的是随机信道目标的最优估计波形设计问题,即设计一种波形,使得在该发射波形下雷达能够更快更准确地完成对目标的估计。随机信道目标,即雷达每次照射时,目标冲激响应为随机过程的一个样本函数,即t~CN(0 ,Rt)。
假设杂波也服从高斯分布,c~CN(0 ,Rc),因此,估计子t和量测信息x是服从联合高斯分布的,即,且y~CN (μy,Ry)。因此,根据式(4)和(5)可求得联合分布的均值和协方差矩阵分别为:
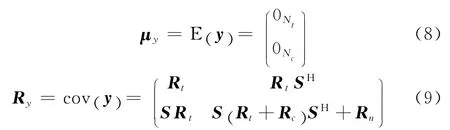
接着通过(6)的最小后验期望损失估计公式求取目标冲激响应的估计值:
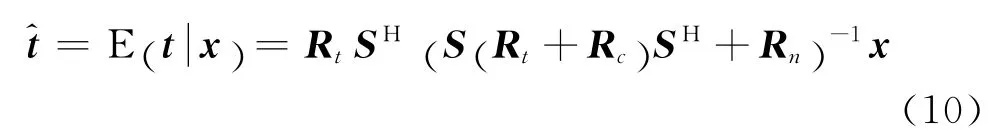
然后通过估计值进一步根据式(7)得到目标冲激响应估计值的MSE为:
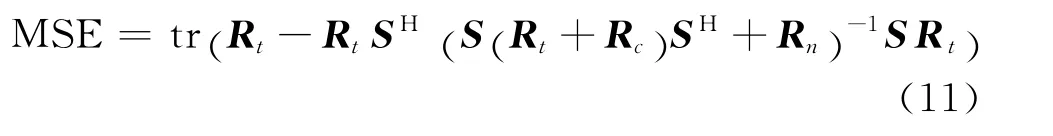
由于MSE是发射波形S的函数,因此可以将基于MMSE的认知雷达估计波形设计问题描述为如下优化问题:
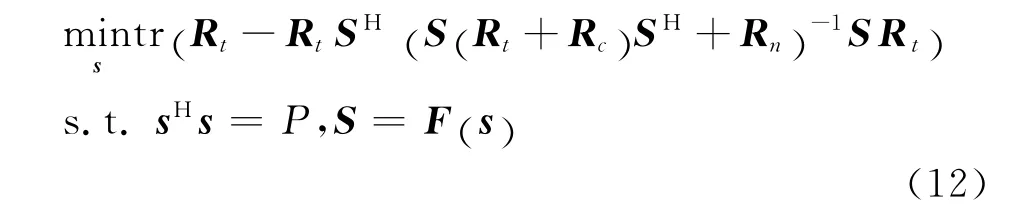
通过目标函数的优化便可求得认知雷达的最优估计波形。
2.2 步骤
结合上述分析将具体步骤描述如下:
第一步:构造联合矩阵,求取相应的均值和协方差矩阵。通过式(8)和(9)分别求取目标冲激响应和接收数据联合分布的均值μy和协方差矩阵Ry。
第二步:计算估计子的估计值。通过式(10)求得对估计误差的任意容许损失函数,目标冲激响应t的最小后验期望损失估计值t^。
第三步:计算估计值的MSE。通过估计值t^进一步根据式(11)得到目标冲激响应估计值的MSE。
第四步:基于最小均方误差(MMSE)准则优化波形。根据矩阵理论相关知识[13]进一步将式(12)的优化问题化简求解便可求得认知雷达的最优估计波形。
3 实验仿真
对优化问题分析求解可知,白噪声背景中,伪随机信号为最优估计波形,色噪声背景中,根据矩阵迹不等式和拉格朗日乘子法可求解得到的最优波形及还原Toeplitz结构的逼近信号。
下面对本文算法进行仿真分析,仿真条件:目标冲激响应和杂波冲激响应长度Nt=Nc=30,离散信号长度Ns=40,所以接收数据和噪声长度Nx=Nn=Nt+Nc-1=69,假设信号的载频、带宽、脉冲重频等发射波形的其他参数都满足雷达要求。功率P与噪声和杂波PSD取同一量级单位(kW),目标和杂波PSD采用随机产生。
实验一:白噪声背景,Rn==0.5。图2为随机产生的目标和杂波PSD采样值;图3显示了MSE与功率P的关系;图4为发射功率等于5 kW时,MSE随发射信号长度Ns变化曲线图。
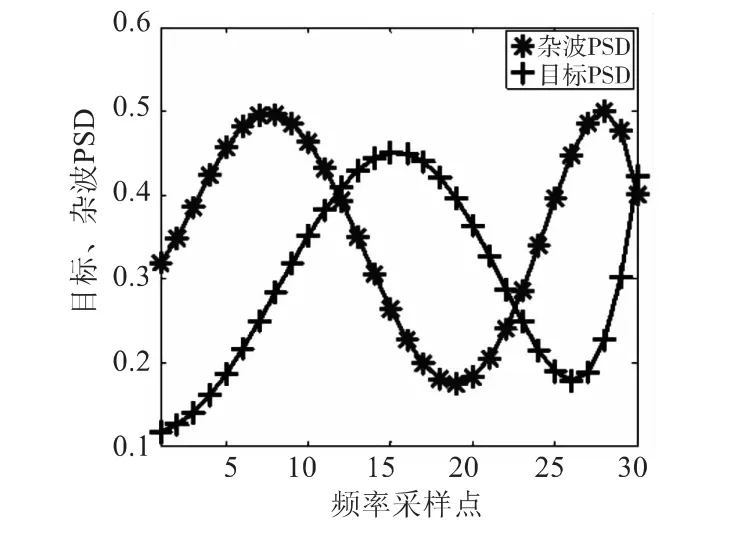
图2 目标、杂波PSDFig.2 The PSD of target and clutter
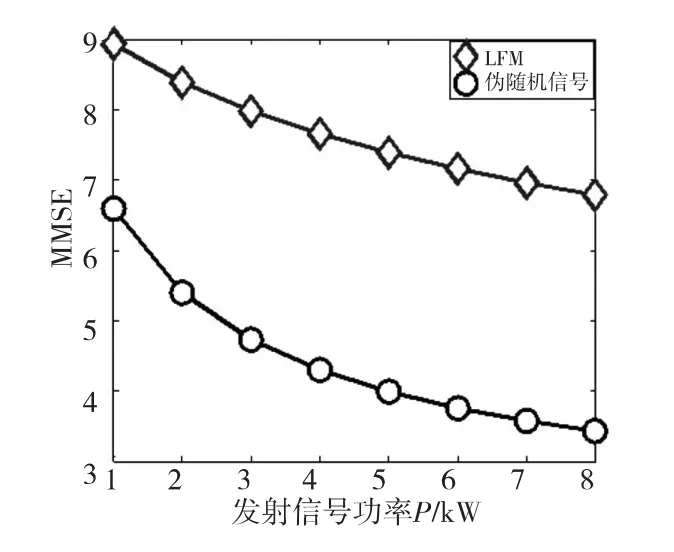
图3 MSE与发射信号功率的关系Fig.3 The MSE versus the power P
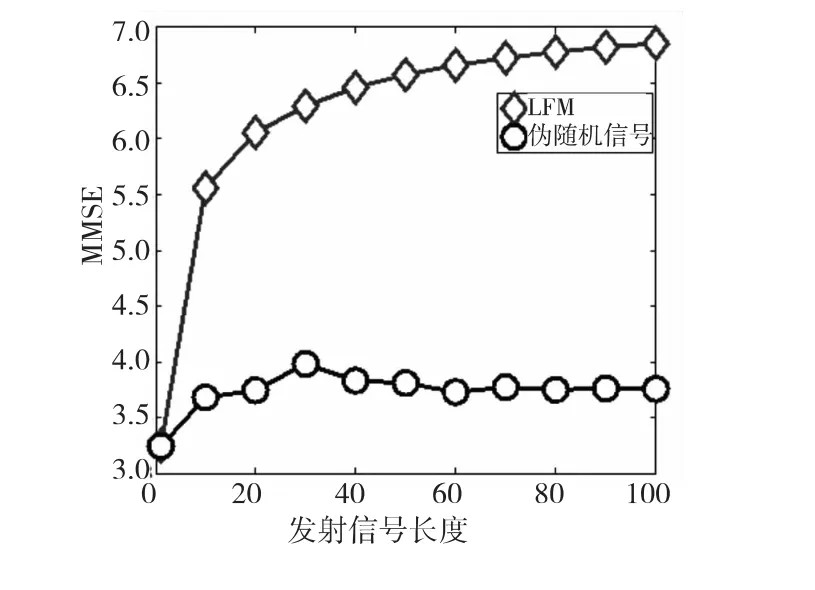
图4 MSE与发射信号长度的关系Fig.4 The MSE versus the length of waveform
由仿真结果可以看出:1)随着发射功率的增加,各个发射波形对应的MSE都逐渐减小,且伪随机信号对应的始终低于常规的LFM信号对应的,这说明伪随机信号的估计性能明显优于LFM信号。2)随着发射信号长度的增加,LFM 信号对应的MSE不断增大,这是由发射功率一定的限制条件引起的。3)当发射信号长度小于40时,伪随机信号对应的MSE存在波动,而大于40以后,基本处于平稳状态。这是由于伪随机信号本身的限制引起的,使得矩阵SHS与PINt的相似度随着发射波形长度的变化而变化。可见,当发射信号长度大于40以后,可以认为此时与发射波形长度无关,且其MSE始终处于LFM下方,这说明伪随机信号在估计性能上远远由于LFM信号。与理论分析一致。
实验二:色噪声背景。图5显示了随机产生的目标、杂波、噪声PSD 采样值σt,i、σc,i、σn,i以及发射信号功率为1kW时求解的信号奇异值σs,i。图6(a)为杂波PSD、噪声PSD之和与目标PSD的比值,图6(b)为信号奇异值的条形图。
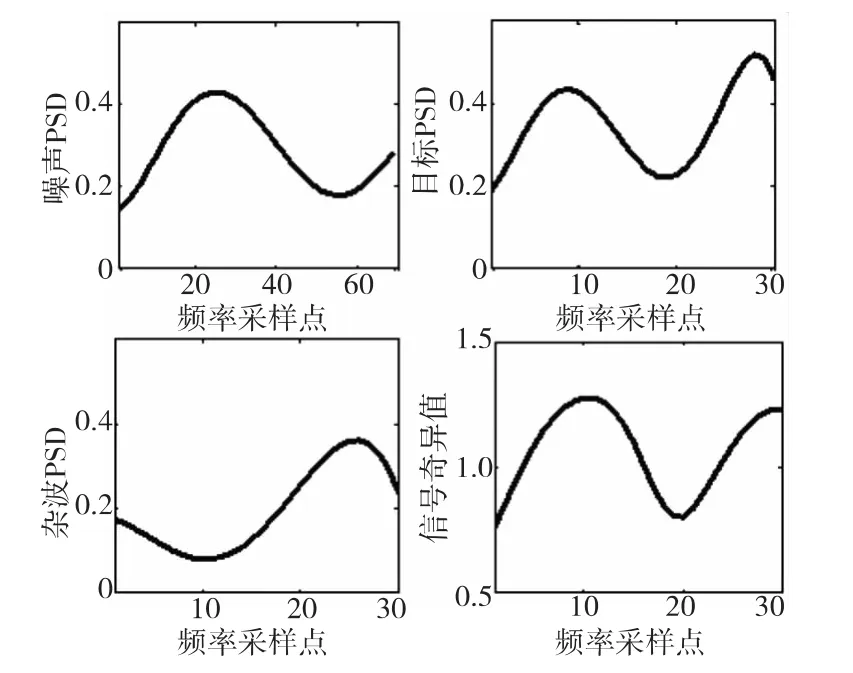
图5 目标、杂波、噪声PSDFig.5 The PSD of target,clutter and noise
由图5和图6可知,本文算法求解的信号奇异值始终与目标PSD呈现相同趋势,与杂波和噪声PSD之和与目标PSD的比值呈现相反趋势,满足了注水原理[8]。这说明优化的发射波形是选择在目标特征较明显的频率分配较多功率,而在杂波、噪声特征较明显的频率分配较少功率,这样,便使得雷达的接收回波能携带更多的目标特征信息。以上结论是经过多次实验验证得到的。
图7显示了LFM信号、上述优化信号Sopt以及逼近信号分别对应的MSE与发射信号功率的关系。
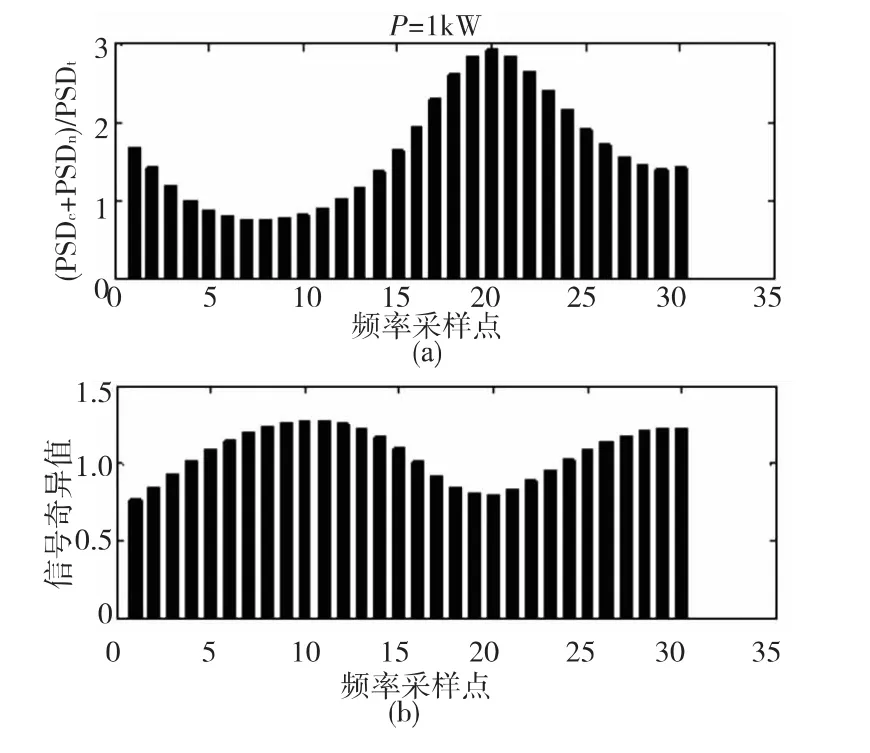
图6 注水原理图解Fig.6 The principle of injection
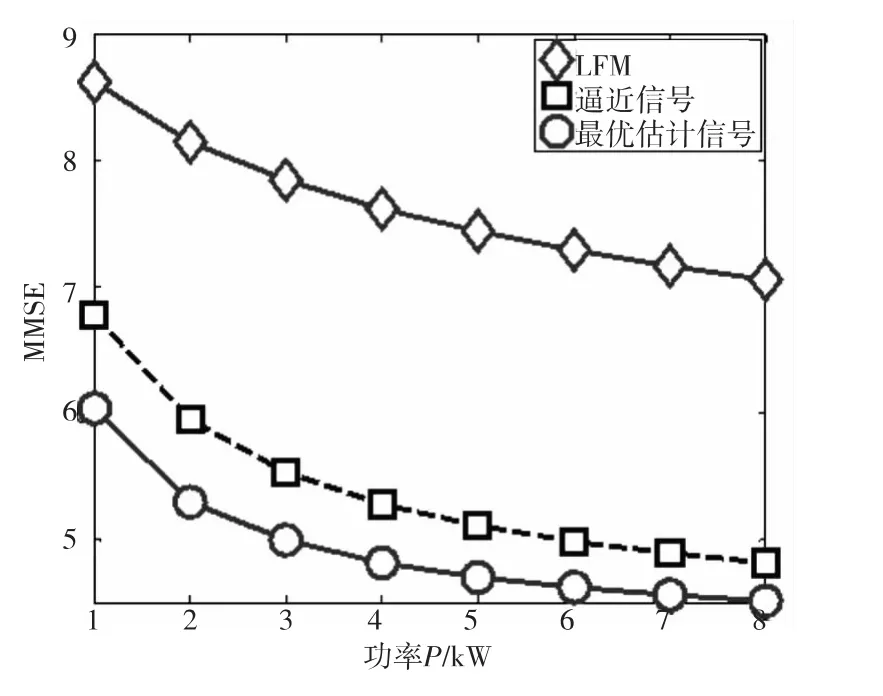
图7 MSE与发射信号功率的关系Fig.7 The MSE versus the power P
由图7仿真结果可知:1)各个发射信号对应的MSE都随发射信号功率的增加而逐渐减小,且本文优化信号对应的始终明显远小于LSM信号;2)逼近信号虽然在性能上略差于最优信号,但相对于常规的LFM信号仍有较大的优势,这说明了逼近方法的可行性。同时逼近信号恢复了信号卷积矩阵的固有Toeplitz结构,因此比最优信号更有实用价值;4)随着发射功率的增加,逼近信号的MSE越来越靠近最优信号,说明逼近程度直接受发射功率影响。发射功率越大,逼近效果越好。
4 结论
本文基于最小均方误差准则提出了一种针对随机信道目标的认知雷达估计波形设计方法。该方法首先联合观测数据和估计子构造一个新的联合矩阵,接着通过贝叶斯方法在该向量的基础上求取估计子的估计值,然后计算估计值的 MSE,最后基于MMSE准则对发射波形进行优化。仿真结果表明,通过该方法优化的波形,在估计性能上相对于传统的LFM信号具有明显的优势,且证明了白噪声背景中,伪随机信号是最优估计波形;色噪声背景中,根据拉格朗日乘子法和矩阵迹不等式求解得到的最优波形,满足注水原理。
[1]Haykin S.Cognitive radar:A way of the future[J].IEEE Signal Processing Magazine,2006,23(1):30-40.
[2]公绪华,孟华东,魏轶旻,等.杂波环境下面向扩展目标检测的自适应波形设计方法[J].清华大学学报(自然科学版),2011,51(11):1652-1656.GONG Xuhua,MENG Huadong,WEI Yimin,et al.A-daptive waveform design for rang-spread detection in clutter[J].Journal of Tsinghua University(Science and Technology),2011,51(11):1652-1656.
[3]Bell M R.Information theory and radar waveform design[J].IEEE Transactions on Information Theory,1993,39(5):1578-1597.
[4]纠博,刘宏伟,胡利平,等.针对目标识别的波形优化设计方法[J].电子与信息学报,2009,31(11):2585-2590.JIU Bo,LIU Hongwei,HU Liping,et al.A method of waveform design for the recognition of radar targets[J].Journal of Electronics &Information Technology,2009,31(11):2585-2590.
[5]范梅梅,廖东平,丁小峰,等.基于 WLS-TIR的多目标识别认知雷达波形自适应方法[J].电子学报,2012,40(1):73-77.FAN Meimei,LIAO Dongping,DING Xiaofeng,et al.Adaptive waveform design based on WLS-TIR for multiple targets recognition in cognitive radar[J].Acta Ekectronica Sinica,2012,40(1):73-77.
[6]王宏强,夏洪恩,程永强,等.基于 MPDA的波形自适应目标跟踪[J].系统工程与电子技术,2011,33(11):2389-2392.WANG Hongqiang, XIA Hong'en, CHENG Yongqiang,et al.Adaptive waveform selection for target tracking based on MPDA[J].Systems Engineering and Electronics,2011,33(11):2389-2392.
[7]韩崇昭,朱洪艳,段战胜,等.多源信息融合[M].北京:清华大学出版社,2006:17-19.
[8]Yang Y,Blum R S.MIMO radar waveform design based on mutual information and minimum mean-square error estimation[J].IEEE Transactions on Aerospace and E-lectronic Systems,2007,43(1):330-343.
[9]Guo D,Shamai S,Verdu S.Mutual information and minimum mean-square error in Gaussian channels[J].IEEE Transactions on Information Theory,2005,51 (4):1261-1282.
[10]NaghibiT,Behnia F.MIMO radar waveform design in the presence of clutter[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(2):770-781.
[11]Ohno S,Giannakis G B.Capacity maximizing MMSE-optimal pilots for wireless OFDM over frequency-selective block rayleigh-fading channels[J].IEEE Transactions on Information Theory.2004,50(9):2138-2145.
[12]Dai F Z,Liu H W,Wang P H,et al.Adaptive waveform design for rang-spread target tracking[J].IET E-lectronics Letters,2010,46(11):793-794.
[13]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004:68-69.
