基于线性分组码的伪随机交织识别
2013-12-01杨晓静
廖 斌,张 玉,杨晓静
(解放军电子工程学院,安徽 合肥 230037)
0 引言
在数字通信中,信道中的噪声和干扰将引起通信系统的性能恶化,交织技术由于具有抵御突发错误的能力而得到广泛应用[1-4],这使得交织识别成为信息截获领域实现信息还原的必不可少的步骤。现有交织主要分为行列式交织、卷积交织和伪随机交织。目前,关于交织识别的研究主要集中在行列式交织和卷积交织的交织长度和交织起始点的盲识别上。文献[5]首先提出了基于“秩准则”的行列式交织的交织长度的盲识别;文献[6—7]在文献[5]的基础上通过引入高斯消元法提高了识别算法的容错性,使之更适用于实际情况;文献[8—10]讨论了卷积交织的参数盲识别问题。可见,已有的文献主要集中在行列式交织和卷积交织这两种交织器的的盲识别上,而对伪随机交织的识别研究未见报道。因此,本文提出的基于线性分组码的伪随机交织识别算法具有重要的意义。
1 基于线性分组码的伪随机交织识别基础
交织中常用的纠错编码包括线性分组码、卷积码、RS码等。(n,k)线性分组码是指将每k个信息位分为一组,通过编码矩阵G变成长度为n(n>k)位的编码,监督位是信息位的线性组合,监督位数位(n-k)。
1.1 “秩准则”算法
“秩准则”算法根据交织中线性分组码的信息码元与监督码元的线性相关性,通过将截获码元序列排成列数不同的矩阵并求秩,寻找缺秩矩阵所对应的列数及截获序列的起点来识别交织长度和交织起始点。
1.2 反转误码率最小准则
反转误码率最小准则主要应用于信号速率盲监测[11]。反转误码率最小准则是指将截获序列按可能的编码、交织等方式等进行译码、解交织处理后再按对应的方式进行编码、交织,将所得的新序列与原截获序列进行比较,选择使两个序列中相异码元数最小即反转误码率最小时所对应的编码、交织方式作为截获序列的编码、交织方式。
1.3 伪随机交织器原理
一个长度为N的交织器在数学上可以描述为一个N 阶置换[1-2]。设∏N表示一个N 阶置换,即

其中,1≤∏i≤N (0≤i≤1),且∏i≠∏j(i≠j)。
m序列常用于伪随机交织器的设计。基于m序列的伪随机交织就是通过m序列产生的伪随机序列作为交织器的地址索引完成序列的置换。移位寄存器每移位一次,n个寄存器输出的数据构成一个状态,一个状态对应一个信息符号。因为m序列是周期为p=2n-1的周期序列,所以交织长度L就是m序列的周期p。这样共有p个信息符号对应m序列p个状态,将这p个状态转化为十进制数,再对这些十进制数按照某一规律进行置换,将它们对应的信息符号按照这个置换顺序发送,就实现了伪随机交织。例如,3级移位寄存器的特征多项式为f(x)=1+x+x3,产生的一个周期m序列为:1 0 1 1 1 0 0,则该 m 序列升序交织示意图如图1所示。
1.4 识别模型
假设信道为二元对称信道(BSC),信道误码率为Pe(0≤Pe≤0.5)。
记截获到的数据序列为Z={z1,z2,…,zn},发送端的数据序列为C={c1,c2,…,cn},信道误码图案为E={e1,e2,…,en},则有

式(2)中,⊕表示模2加。
在信息截获中,侦察方并不知道截获数据序列的交织参数,本文研究的内容就是根据截获的Z,通过分析识别出其交织长度、交织起始点和交织置换关系,完成伪随机交织识别,从而恢复出原始数据C。
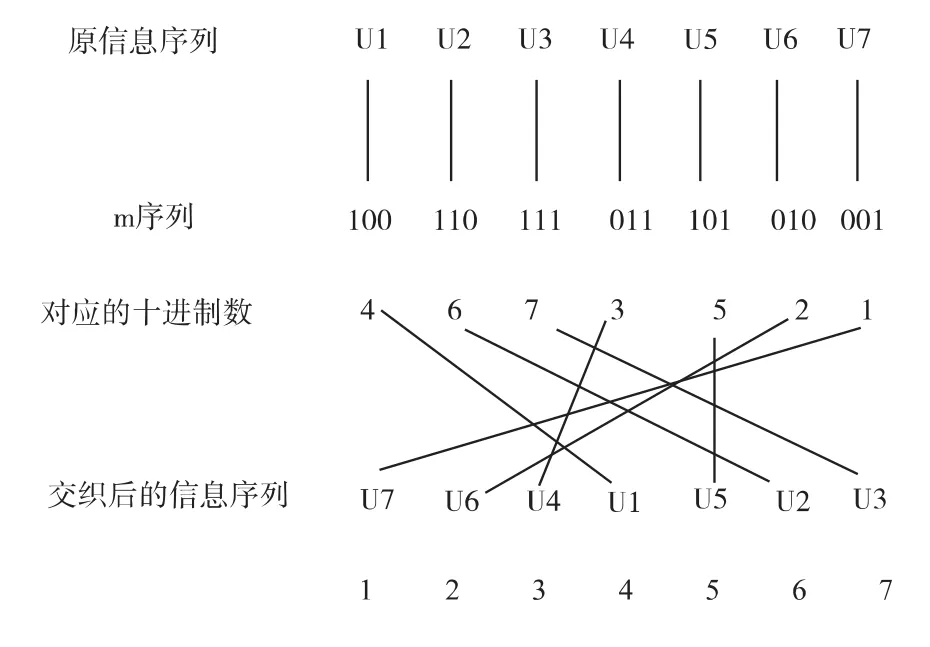
图1 交织长度为7的m序列伪随机交织器Fig.1 The m sequence pseudo-random interleaver with the interleaving sizeof 7
2 基于线性分组码的伪随机交织识别
基于线性分组码的伪随机交织识别包括对交织长度、交织起始点和交织置换关系的识别。2.1节利用“秩准则”识别伪随机交织的交织长度和交织起始点,2.2节利用反转误码率最小准则实现伪随机交织器的交织置换关系的识别。
2.1 交织长度和交织起始点的识别
本小节利用“秩准则”实现对伪随机交织的交织长度和交织起始点的识别。根据所采用的纠错码的性质和交织器的特点,寻找由截获到的序列构成的数据分析矩阵中最大数目的“相关列”[7],根据取到最大的“相关列”所对应的数据分析矩阵的列数及截获序列的起点作为交织长度和交织起始点。
例如,(n,k)线性分组码是由一个满秩的生成矩阵G将k bit的信息码元编成n bit的纠错码元。

其中,Pn-k称作该(n,k)线性分组码的监督矩阵,pij∈ {0,1}(1≤i≤k,1≤j≤n-k)。由C=M·G可知,
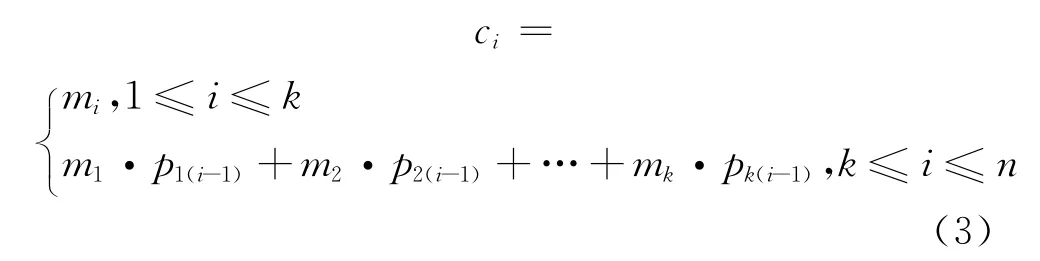
由式(3)可知,生成的码序列C中的一部分码元ci是其他码元的线性组合,而交织器的作用只是改变序列中码元的位置,并不改变信息内容。因此,线性分组码经过交织后这种性质仍然存在。将截获的信息序列排成一个列值为na的数据分析矩阵A。可以发现,当数据分析矩阵A的列值na与交织长度L相等,或为交织长度L的整数倍,即满足na=a·L(a∈N+)时,由于监督码元恰好都处在同一列上,这样数据矩阵具有缺秩的特性,即
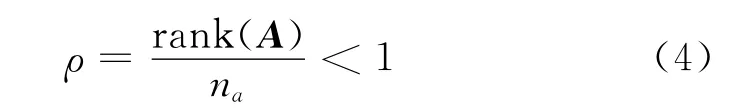
而当数据矩阵A的列值na与交织长度L不满足相等或倍数的关系时,此时的A是一个二元随机混排矩阵,它的秩为1,如图2所示(图中,监督码元所在位置用灰色标注),据此可以得到交织长度L。而当数据矩阵A的第一个元素恰好是交织序列的起始点时,这时ρ将取到最小值,故可以在得到交织长度L的条件下,再遍历寻找序列移位时使ρ最小的移位量,从而找到交织起始点d。
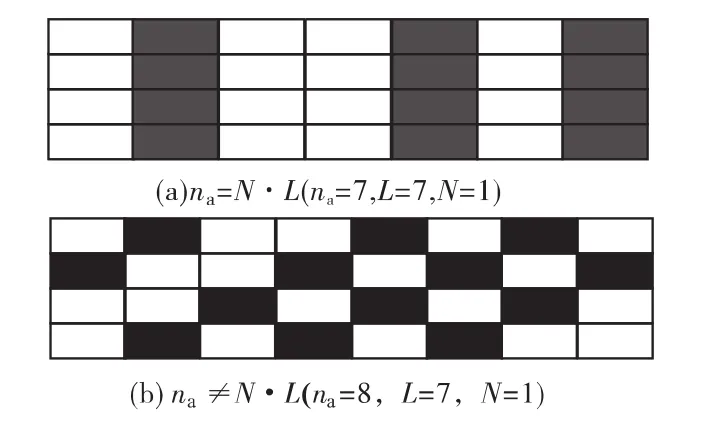
图2 不同列值na下的数据分析矩阵ig.2 The data analysis matrix withdifferent columns of na
当信道中存在误码时,由于误码的影响,可能使得“相关列”间的约束关系被破坏而不能正确估计交织长度,本文采用有限域上的高斯约当消元法[7]进行改进。具体做法是将数据矩阵A化成下三角阵AL,根据下三角阵AL的下半部分ALd的列向量的汉明重量计算Q(Q为满足有误码的门限条件下的相关列的列数),Q的计算公式为[7]:
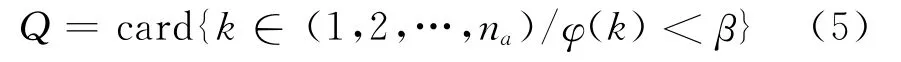
其中,card{·}表示集合的势,φ(k)是矩阵ALd的第k列的汉明重量与ALd所有列向量的汉明重量的均值的比值,β为检测门限。检测门限β的选取与误码率有关,通常选取的检测门限β为(0.2,0.6)[6-7]。
定义:矩阵ALd中Q与总列数na的比值为x,

由前面的分析可知,当x取到最大值时,此时的数据分析矩阵列数na就为所要识别的交织长度L,数据分析矩阵列数na的第一个码元所在位置定为交织起始点,由此实现对伪随机交织长度和交织起始点的识别。
2.2 伪随机交织置换关系的识别
由1.3节分析的基于m序列的伪随机交织的原理可知,决定伪随机交织置换关系的是伪随机交织器中m序列的长度和产生m序列的线性反馈移位寄存器(LFSR)中各寄存器的初态。由于伪随机交织的特点,特别是在截获数据长度有限或交织长度较大的情况下,直接观察出交织置换规律很困难。本文借鉴通信系统中用于速率盲监测的方法[8],提出一种基于反转误码率最小准则下的伪随机交织置换关系识别方法。
在2.1节中,已经得到了伪随机交织的长度和交织起始点,在此基础上,根据p=2n-1反推得到线性反馈移位寄存器(LFSR)的级数p,则该LFSR的初态共有2p-1个(全0状态排除)。设LFSR的初态集合为I= {I1,I2,…,I2p-1},因为伪随机交织置换关系由LFSR中各寄存器的初态决定,则对应的交织置换关系共有2p-1种,设交织置换关系的集合为S= {S1,S2,…,S2p-1}。对一个周期为L =2p-1的伪随机交织器,其LFSR所用的初态Ik必有Ik∈I,其对应的交织置换关系必有Sk∈S。根据交织长度L=2p-1寻找可能的编码方式B={B1,B2,…,BR},则必有截获序列所用的编码方式Bj∈B,则交织与编码相结合的方式共有R·(2p-1)种。
遍历R·(2p-1)种交织与编码相结合的方式对截获序列Z进行解交织、译码后得到R·(2p-1)种信息序列C′= {C′1,C′2,…,C′R·(2p-1)}。对得到的信息序列C′再根据译码方式进行对应的编码、交织得到R·(2p-1)种对应的编码序列Z′= {Z′1,Z′2,…,Z′R·(2p-1)}。 将 Z′ = {Z′1,Z′2,…,Z′R·(2p-1)}与截获序列 Z进行模2和运算,得到的反转误码率(RESR)集合为 W′ = {W′1,W′2,…,W′R·(2p-1)}。当编码方式与交织置换关系识别错误时,所得到的C′进行再编码、交织所得的编码序列Z′可看做一个随机序列,其与原截获序列Z比较所得的反转误码率(RESR)较大;而当编码方式和交织置换关系识别准确时,所得到的C′进行再编码所得的编码序列Z′与原截获序列Z基本相同,两者之间的反转误码率(RESR)很小。因此,求使式(7)最小的(Bj,Sk)中的Sk即为所求的交织置换关系。
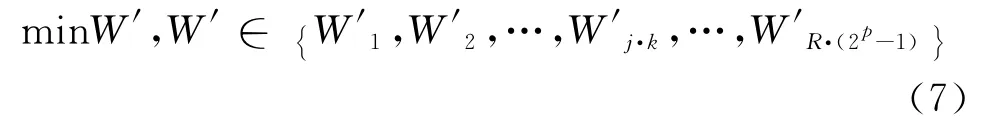
2.3 算法步骤
基于线性分组码的伪随机交织识别算法包括两个部分:识别交织交织长度和交织起始点和识别交织置换关系识别。
1)识别交织长度和交织起始点
设定检测门限β,na的最小检测值为namin、最大检测值为namax,na从namin到namax变化,d从0到na-1变化,两个识别参数构成二维循环,每次循环中进行如下步骤:
步骤1设初值:设Q的初始值为0,Q与na的比值x为0;
步骤2预处理:将截获序列排成数据矩阵并通过高斯约当消元法化成下三角阵AL;
步骤3求列汉明重量和均值:取下三角阵的下半部分ALd计算各列的汉明重量,并求出均值;
步骤4比较、记录:由公式(5),(6)计算Q和x,并记录对应的na,d。
当所有循环结束时,寻找最大的x和对应的na,d,得到交织长度和交织起始点值。
2)识别交织置换关系
步骤1求交织置换关系集合:由识别出的交织长度反推得到LFSR的级数p和对应的交织置换关系的集合S= {S1,S2,…,S2p-1};
步骤2遍历解交织、译码:遍历R·(2p-1)种交织与编码相结合的方式对截获序列Z进行解交织、译码,得到R·(2p-1)种信息序列C′= {C′1,C′2,…,C′R·(2p-1)};
步骤3求反转误码率:对C′进行再编码、交织得到Z′,与Z进行模2和运算得到反转误码率集合W′;
步骤4匹配置换关系:寻找使式(7)最小的Sk,判定为交织置换关系。
3 仿真实验
由于篇幅限制,本文研究的前提条件是假定编码方式已经得到识别,对编码方式的识别不再讨论。
仿真实验1:验证算法的有效性。仿真实验采用(15,7)线性分组码,采用4级的LFSR,特征多项式为f(x)=x4+x+1,置换关系对应的寄存器初态为(0001),截获序列Z的首位是发送端序列C中的第9位,即交织起始点d=9,检测门限β=0.5,误码率Pe=0.001。交织长度与交织起始点的仿真识别结果如图3,交织置换关系的仿真识别结果如图4。
图3表明:在交织长度为15,交织起始点为9的情况下,x=0.600为最大值,与实验条件一致,表明识别正确。图4表明:在置换关系对应的初态(0001)时,反转误码率最小,识别结果与实验条件相同,识别正确。
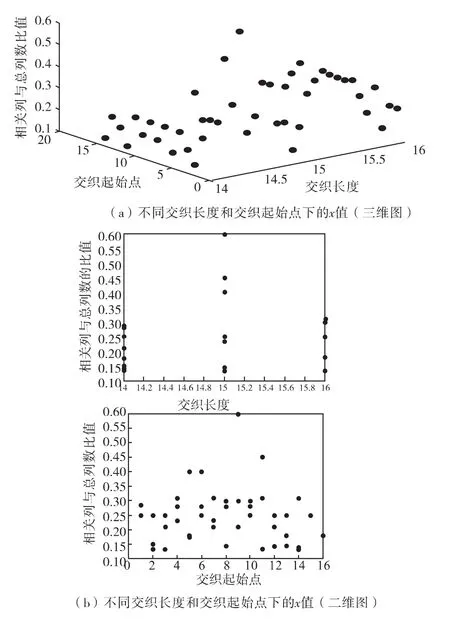
图3 不同交织长度和交织起始点下的x值Fig.3 The values of x with different interleaving size and interleaving delay
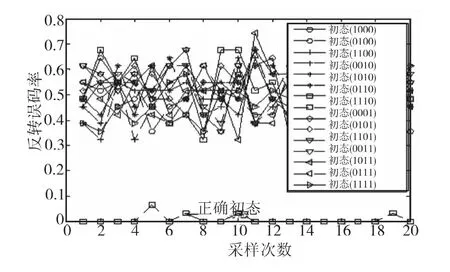
图4 置换关系识别结果Fig.4 The result of the recognition about interleaving permutation
仿真实验2:算法容错性能比较。仿真实验采用(7,3)线性分组码,采用6级的LFSR,特征多项式为f(x)=x6+x+1,置换关系对应的寄存器初态为(000001),截获序列Z的首位是发送端序列C中的第9位,即交织起始点d=9,检测门限β=0.5。误码率Pe从0到0.02,以0.001为步进变化,仿真结果如图5所示。
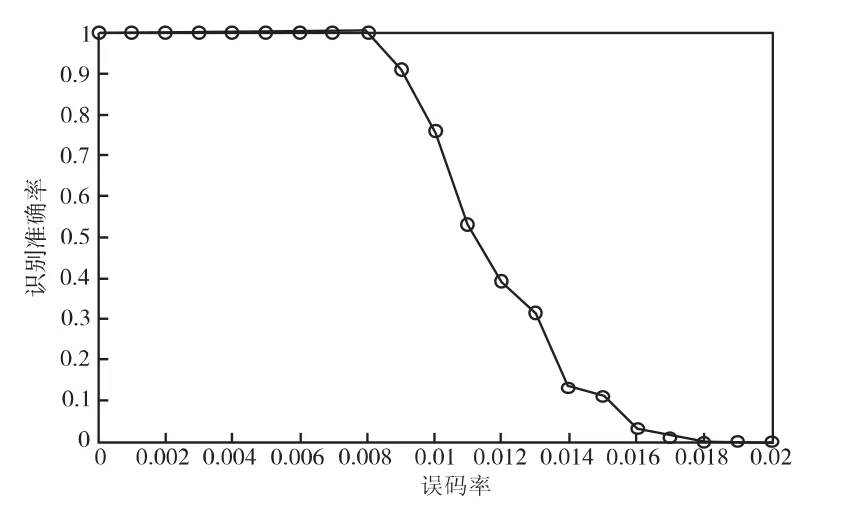
图5 不同误码率下的识别正确率Fig.5 The accuracy of recognition with different bit error rates
由图5可知,本文方法在误码率小于0.008时的识别准确率可达100%,当误码率达到0.009时,其识别准确率超过90%,误码率在0.01时,识别准确率在75%以上,具有较好的容错性能。
4 结论
本文提出了基于线性分组码的伪随机交织识别算法,首先利用“秩准则”识别交织长度、交织起始点,在此基础上提出反转误码率最小准则识别交织置换关系。仿真实验结果表明了本文方法在误码率小于0.008时的识别准确率可达100%,当误码率达到0.009时,其识别准确率超过90%,误码率在0.01时,识别准确率在75%以上,具有较好的容错性能。
[1]John G.Proakis.Digital Communications(Fourth Edition)[M].Beijing:Publishing House of Electronics Industry,2008:467-469.
[2]Ramsey J L.Realization of optimum interleavers[J].IEEE Transactions on Information Theory,1970(3):338-345.
[3]Forney G Jr.Burst-correcting codes for the classic bursty channel [J].IEEE Transactions on Communication Technology,1971,19(5):772-781.
[4]张永光,楼才义.信道编码及其识别分析[M].北京:电子工业出版社,2010:108-117.
[5]Burel G,Gautier R.Blind estimation of encoder interleaver characterstics in a non-cooperative context[C]//Proceedings of the IASTED International conference on communication,Internet and Information Technology Scottsdale,AZ,USA:ACTA Press,2003.275-280.
[6]Guillaume Sicot,Sbastien Houcke.Blind detection of interleaver parameters.Proceeding of the ICASSP 2005[C].Philadephia,USA:IEEE Press,2005.829-832.
[7]Guillaume Sciot,Sebastien Houche,Johann Barbier.Blind detection of interleaver parameters[J].Signal Processing,2009,89(4):450-462.
[8]Liru Lu,Kwok Hung Li,Yong Liang Guan.Blind identification of convolutional interleaver parameters [C]//ICICS 2009proceedings of 7thInternational conference on Information,Communications and Signal Processsing.Piscataway,NJ,USA:IEEE Press,2009,1-5.
[9]甘露,刘宗辉,廖红舒,等.卷积交织参数的盲估计[J].电子学报,2011,39(9):2173-2177.GAN Lu,LIU ZhongHui,LIAO HongShu,et al.Blind estimation of the parameters of convolutional interleave[J].Acta Electronica Sinica,2011,39(9):2173-2177.
[10]张玉,张伟杰,杨晓静.数字通信中卷积交织盲识别方法[J].电讯技术,2011,51(5):62-66.ZHANG Yu,ZHANG WeiJie,YANG XiaoJing.A blind recognition method of convolutional interleaving in digital communication[J].Telecommunication Engineering,2011,51(5):62-66.
[11]刘胜美,赵春明,李灿伟.盲速率判决技术在OFDM系统中的应用[J].电子与信息学报,2006,28(3):396-399.LIU Shengmei,ZHAO Chunming,Li Canwei.Blind rate detection applied in the IPR-OFDM system [J].Journal of Electronics & Information Technology,2006,28(3):396-399.
