存在边界流时压力溶解对颗粒聚集岩体中THM耦合作用的有限元模拟

张玉军，杨朝帅,

(1. 中国科学院 武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉，430071)2. 中国中铁隧道集团有限公司 技术中心，河南 洛阳，471009)

当地热田或高放射性核废物处置库位于地层深部的高温、高压及富水环境中时，对于孔隙−裂隙岩体而言，存在明显的压力溶解作用[1]，其主要使得岩体的孔隙率和渗透系数减少，从而对热−水−应力−化学耦合过程产生影响。对此，国外已经进行较多的研究[2−6]。其中，Yasuhara等[7]通过室内试验，提出一种表现压力溶解三过程的数学模型；Taron等[8]基于Yasuhara的工作，将压力溶解、热−水−应力收缩与膨胀、矿物沉淀与溶解对裂隙开度张开与闭合的复杂影响进行数学简化，并以此结合 TOUGHREACT和FLAC3D软件分析天然裂隙岩体的渗透率变化机理；Taron等[9−10]还考虑拟静水或有边界流的情况，发展一种新的压力溶解模型，并将其应用于具有动态渗透率的裂隙岩体工程地热库中耦合的力学和化学过程的数值模拟。上述压力溶解模型具有很高的学术价值和实用价值，但目前尚未见将其用于颗粒聚集体孔隙介质的多场耦合数值分析中，而这种分析对于在诸如岩盐、黏土类岩体中进行高放废物地质处置等环境工程有着重要的指导价值。为此，本文作者建立压力溶解模型，引入所研制的岩土介质热−水−应力耦合有限元分析程序中(对其中的体积应变求解式进行一定修正)，给出颗粒聚集体孔隙率随压力溶解和渗透系数随孔隙增缩的演化表达式，在计算时对孔隙率和及渗透系数实施动态调整。以1个假定的位于饱和地层中的高放废物地质处置库为算例，在相同的初始温度和岩体应力条件下，针对2种计算工况即边界上水压力相同(域内无因边界水头差产生的稳态流量，工况1)和左、右边界上水压力有较大差别(域内有因边界水头差产生的稳态流量，工况2)，进行热−水−应力耦合有限元数值模拟，考察处置库近场的温度、颗粒界面水膜及孔隙中的溶质浓度、迁移和沉淀质量、孔隙率和渗透系数、孔隙水压力、地下水流速、应力的变化、分布情况。

1 混合质量平衡

对于如图1和图2所示的颗粒聚集体化学压缩模型，Taron等提出物质在压力作用下的溶解浓度平衡关系[10]：

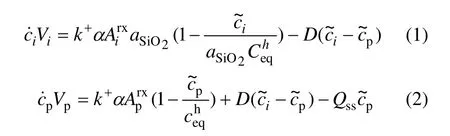
图1 孔隙介质、裂隙及化学压缩过程的概念化[10]Fig. 1 Conceptualization of chemical compaction process,porous media, and fractures[10]

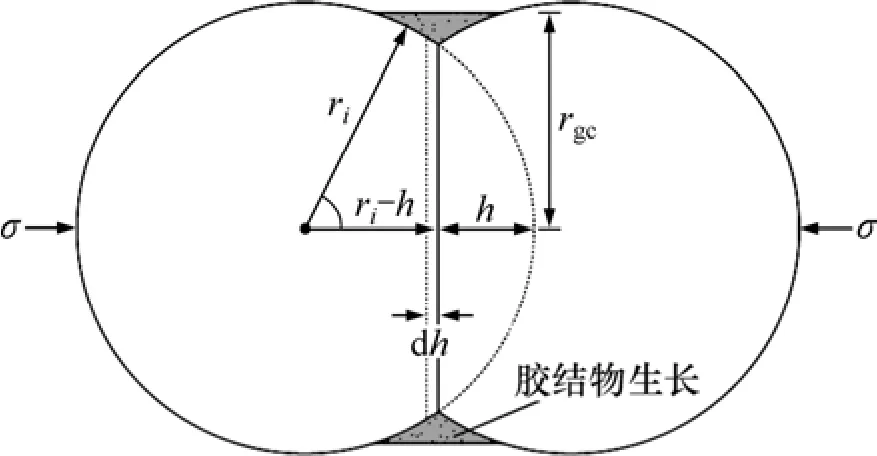
图2 压缩及颗粒和生长的胶结物半径的关系示意[10]Fig. 2 Diagram of compaction and relationship between granular and growing cement radius[10]

其迭代求解式为

式中：ci是在颗粒接触面水膜中溶解硅的即时浓度；cp是在颗粒周界(孔隙空间)处的即时硅浓度；k+是溶解速率常数；α为固体接触部分所占据的颗粒边界的比例(0≤α≤1)；为表征体颗粒交界处的反应面积(REV)；为液态水中硅的溶解度；D为扩散系数；Vi是颗粒接触之内表征体的体积(REV)；为表征体的孔隙反应面积(REV)；Vp为表征体的孔隙体积(REV)；aSiO2为应力作用下固体硅的化学活度；Qss为因边界水头差产生的稳态流量；Δt为时间增量。

式(1)中各物理量可表示为：

式中：V0和V分别为表征体(可取单位量)的初始和即时体积；0φ和φ分别为初始和即时的孔隙率；Sag和Vg分别为平均的单个颗粒表面积和体积；ag为2个相互贯穿球形颗粒的接触面积；Nc为每个颗粒的接触数；Df为分子扩散系数；ω为颗粒接触面水膜的厚度；Δμ为化学势梯度；R这气体常数；T为绝对温度。

并且有

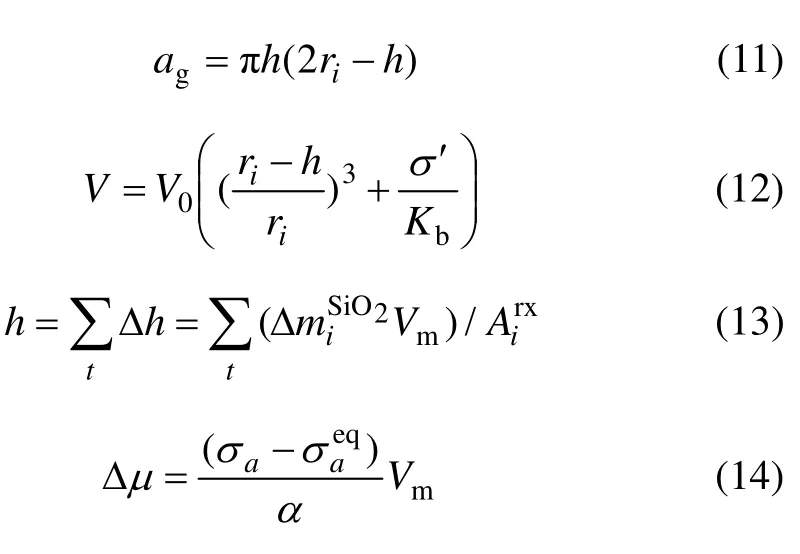
式中：ri为初始时刻的平均颗粒半径；h为累积的球形颗粒贯穿深度(初值为0)；σ′为有效应力；Kb为颗粒材料的体积模量；为产生于颗粒接触面处的迁移质量(以溶解的数值为正)；Vm为固体的摩尔体积。

而

式中：σa和分别是真实应力及达到平衡时的临界应力；Rc为接触面积比；EA和TA分别为熔化热和熔化温度；βc为埋置常数，rgc为颗粒交界处沉淀胶结物外表面到颗粒中心连线的距离(如图2所示)。

2 孔隙率−渗透系数演化律

Taron等给出的孔隙率表达式为

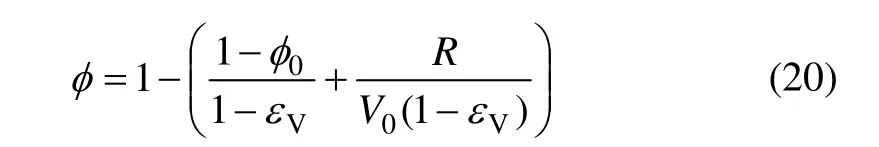
式中：εV为有限的体积应变；R为作为源/汇项的随时间求和的反应体积。

并且

由此可求出对应的渗透系数为[11]

式中：k0初始时刻的渗透系数。

将上述颗粒聚集体的压力溶解模型引入文献[12]的孔隙介质热−水−应力耦合有限元程序中。

3 算例

实验室尺度的核废料玻璃固化体埋置模型如图 3所示，其周围的介质是饱和的石英颗粒聚集孔隙岩体。作为近似简化，认为这是一个平面应变问题。取计算域为水平向4 m，垂直向8 m，有800个单元，861个节点。从固化体边缘向右的点号依次为432，433，434，435和436。

对于边界条件，计算域的顶面位移自由，其上作用有分布荷载53.4 MPa；左、右侧面的水平方向位移约束；底面的垂直方向位移约束；所有边界的温度为40 ℃；对于工况 1，各边界的孔隙水压力均为4.59 MPa；对于工况 2，左、右边界的孔隙水压力分别为4.59和2.295 MPa，而上、下边界的孔隙水压力在这二者之间线性过渡，岩体的初始孔隙率为0.3。热−水−应力耦合的环境对岩体颗粒要产生压力溶解作用，从而引起孔隙率和渗透系数的变化。有关的计算参数如表 1和表 2所示(该表中主要数据参考文献[1，10])。初始状态时，岩体的温度均为40 ℃。核废物以1 kW的不变功率释放热量，时间经历4 a。

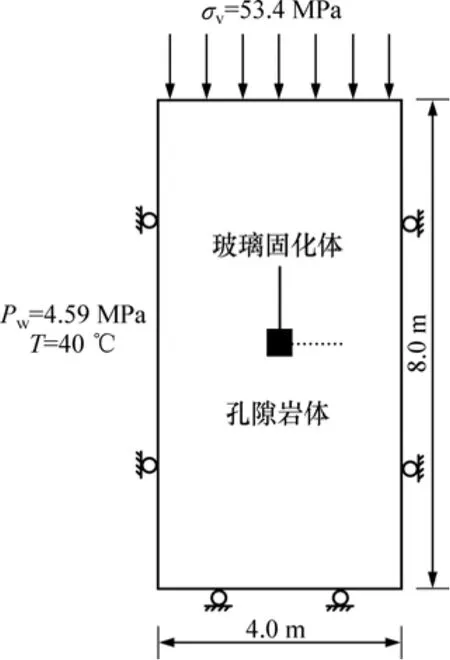
图3 计算模型(工况1)Fig. 3 Computation model(case 1)

岩体介质的水分特性曲线符合van Genuchten模型[13]，即

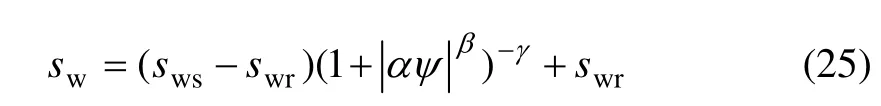
式中：α=3.86×10−6m−1，β=1.41，γ=1−1/β；ψ为水势；sws=1.0，swr=0.19，其分别为最大饱和度和最小饱和度。比渗透率与饱和度的关系为

表1 主要计算参数Table 1 Main computation parameters

表2 压力溶解计算参数Table 2 Parameters for pressure solution

取岩体介质的温度梯度水分扩散系数为Dt=2.5×10−12m2/(s·℃)，针对前述的2种工况，其主要结果及分析如下。

由于渗流和地应力对核废物释热的影响较小[14]，故2种工况条件下计算域中的温度场基本相同。以工况1为例，432，433，434和435各点处的温度随时间的变化曲线如图4所示。从图4可见：在开始的约0.1 a内缓冲层的温度快速上升，之后增加减缓，到计算终时432，433，434和435各点的温度依次为97.8，81.9，72.6和 65.7 ℃。图5所示为工况1在4a时计算域中的温度等值线分布。

图6所示为岩体中2个点的溶质浓度−时间曲线(固化体中心x=0)。从图6可见：在压力溶解作用下，颗粒接触面处和颗粒孔隙中的溶质浓度ci和cp在开始约0.2 a内急速升、降，之后随时间的推移仍在减小，但变化幅度不大。到计算终了时x为0.3 m和1.1 m处的溶质浓度ci分另为14.65 mol/m3和15.03 mol/m3(工况 1)，15.19 mol/m3和 15.27 mol/m3(工况 2)；cp：13.03 mol/m3和 13.04 mol/m3(工况 1)，13.04 mol/m3和 13.05 mol/m3(工况 2)。

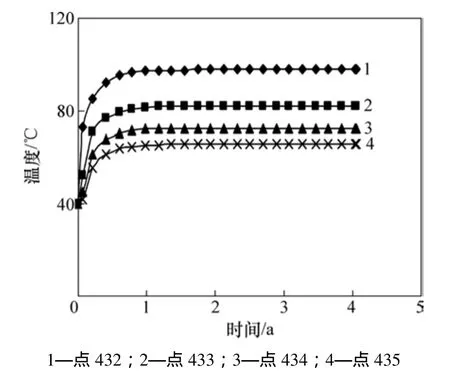
图4 温度−时间曲线Fig. 4 Temperatures versus time at some nodes

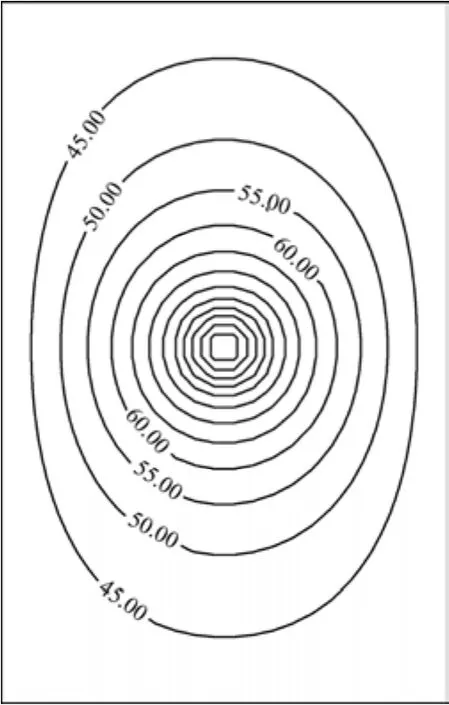
图5 4 a时工况1计算域中温度等值线(单位：℃)Fig. 5 Temperature contours in calculation domain at 4 years (℃)

图6 岩体中2个点的溶质浓度−时间曲线(固化体中心x=0)Fig. 6 Solute concentrations versus time at two nodes (x=0 at center of vitrified waste)

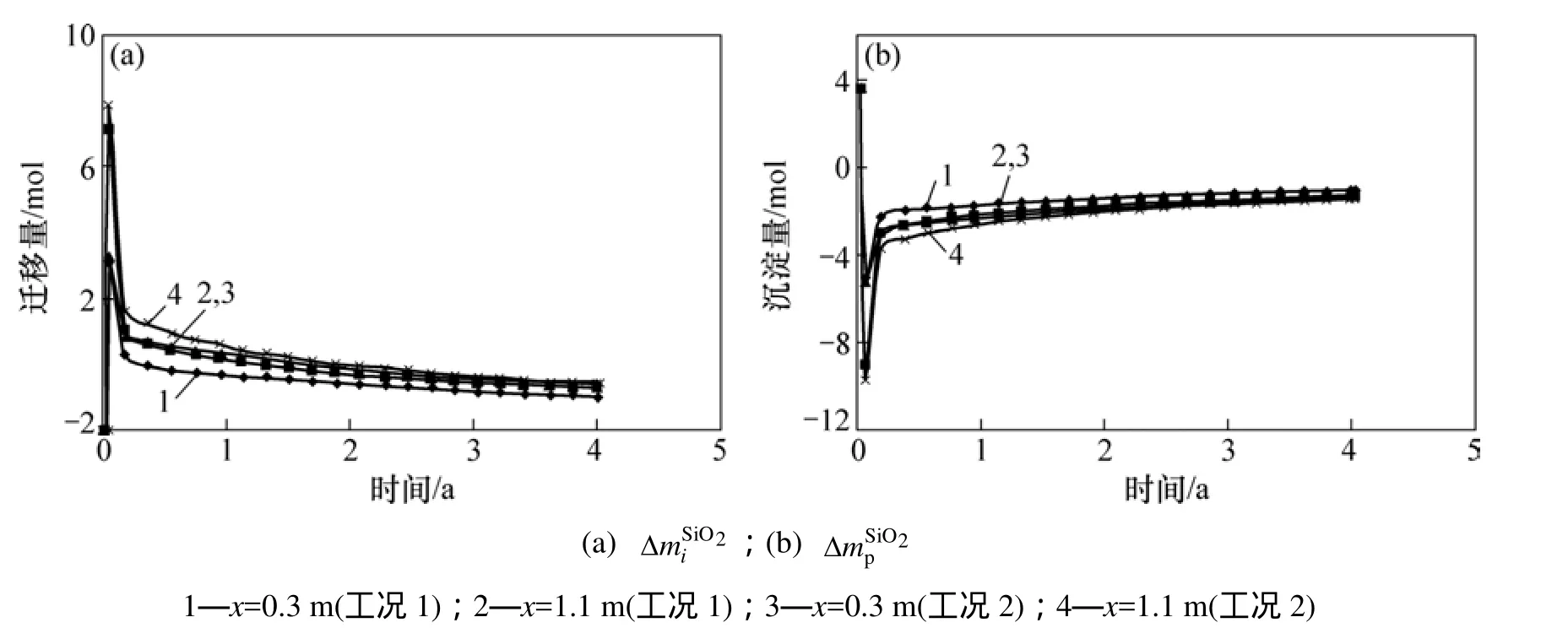
图7 岩体中2个点的迁移/沉淀量−时间曲线(固化体中心x=0)Fig. 7 Removal/precipitation masses versus time at two nodes (x=0 at center of vitrified waste)

图7 所示为岩体中2个点的迁移/沉淀量−时间曲线(固化体中心x=0)。从图7可见：在压力溶解作用下，颗粒接触面处的迁移质量和颗粒孔隙中的沉淀质量亦在开始约0.2 a内急速升、降，之后随时间的变化趋缓。正是因颗粒接触面处的溶解和颗粒孔隙中的沉淀使得岩体孔隙率减小。到计算终了时x为0.3 m和1.1 m处，分别为1.038 11 mol和1.279 06 mol(工况1)，1.379 43 mol和1.430 91 mol(工况 2)；分另为−1.038 13 mol和−1.279 08 mol(工况 1)，−1.379 45 mol和−1.430 94 mol(工况 2)。经比较可知：，即颗粒接触面处的溶解量基本变为颗粒孔隙中的沉淀量。

图8所示为源/汇项反应体积R和颗粒贯穿深度h随时间的变化曲线。从图8可见：在压力溶解作用下，R和h也是在开始约0.2 a内急速上升，之后随时间的推移R缓慢下降，而h还呈现明显的增长趋势(孔隙率减小的原因之一)。到计算终了时x为0.3 m和1.5 m处，R分别为 8.330×10−5m3，8.227×10−5m3(工况 1)，8.341×10−5m3和 8.237×10−5m3(工况 2)；h分别为1.317×10−5m和1.502×10−5m(工况1)，1.512×10−5m和 1.615×10−5m(工况 2)。

图8 岩体中2个点的反应体积和颗粒贯穿深度−时间曲线(固化体中心x=0)Fig. 8 Reaction volumes and granular interpenetrations versus time at two nodes (x=0 at the center of vitrified waste)

图9 2种工况在4 a时岩体中孔隙率等值线分布(单位：10−1)Fig. 9 Contours of porosity in rock mass at four years for two cases

图 9所示为工况 1到 4 a时玻璃固化体周围 2 m×2 m范围内岩体孔隙率等值线分布。此时在计算域水平对称轴上距玻璃固化体中心0.3 m和1.1 m点处的孔隙率分别为 0.181和 0.154(工况 1)，0.145和0.133(工况 2)，分别约为初始值 0.3的 60%，51%和48%、44%。距离玻璃固化体越远，孔隙率减小越多，其原因为：在玻璃固化体附近温度较高，由此产生的热效应使得真实应力σa与临界应力之差较小，并且固体硅的化学活度与温度T成反比，因而，该处孔隙率下降较少，反之亦然。上述2点处的孔隙率随时间的变化曲线如图10所示。从图10可见：在开始的约0.2 a内，因上覆及自重荷载的施加，压力溶解使得岩体孔隙率内急速下降，之后随时间的推移孔隙率虽仍在衰减，但变化幅度较小(渐趋平衡)，且与温度的增长趋势并不同步。将图10与Taron等由解析及试验得出的岩体孔隙率−时间曲线[10](图11)相比较，二者变化趋势较一致。

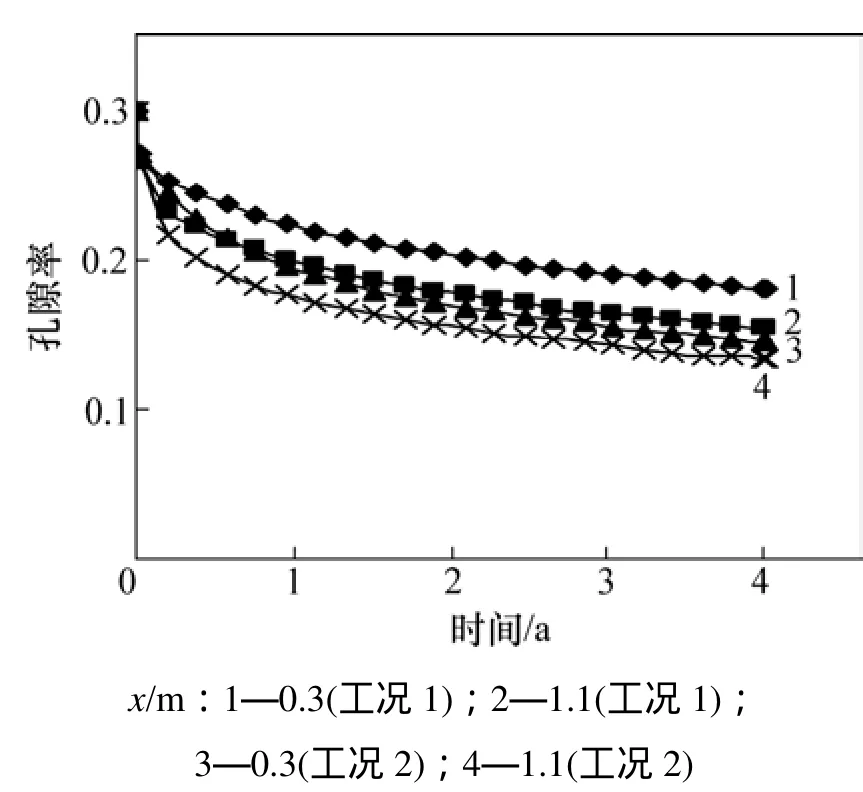
图10 岩体中2个点的孔隙率-时间曲线(固化体中心x=0)Fig. 10 Porosities versus time at two nodes(x=0 at center of vitrified waste)

图11 Taron模型与试验数据的对比[10]Fig. 11 Comparison of Taron model with experimental data[10]

相对应的渗透系数的等值线分布及随时间的变化曲线见分别图12和图13，其与孔隙率的演化规律类似，在时间上表现了一定的非线性特征(由式(22)决定)。上述2点处的渗透系数分别为0.199×10−13m/s和 0.115×10−13m/s(工况 1)，0.093×10−13m/s 和0.070×10−13m/s(工况2)，分别约为初始值的16.0%，9.2%和7.5%，5.6%。

图14所示为2种工况中432和434点处的孔隙水压力随时间的变化曲线。从图14可见：开始时由于岩体荷载突然施加，孔隙水压力有瞬时的少许下降，之后在压力溶解(岩体孔隙率和渗透系数减小)、应力场和温度场的共同作用下，孔隙水压力随时间呈一定幅度上升。到4 a时该432和434点处的孔裂隙水压力分别为4.580 1 MPa和4.580 5 MPa(比初值4.59 MPa略小)(工况1)，3.464 6 MPa和3.217 9 MPa(分别大于初值3.33 MPa和3.10 MPa)(工况2)。计算终了时2种工况中的孔隙水压力等值线如图15所示。

图12 2种工况在4 a时岩体中渗透系数等值线分布(单位：10−14 m/s)Fig. 12 Contours of permeability in rock mass at four years for two cases

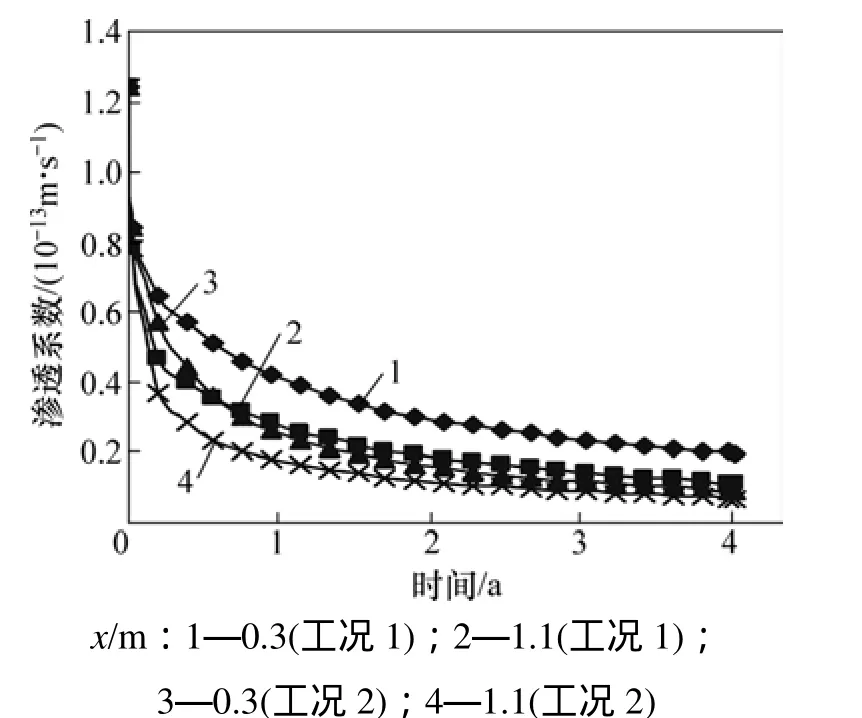
图13 岩体中2个点的渗透系数−时间曲线(固化体中心x=0)Fig. 13 Permeabilities versus time at two nodes(x=0 at the center of vitrified waste)

图16 所示为工况1，2在4 a时计算域中的孔隙水流速矢量分布，前者与后者的比例尺为50:1。看到2种工况的流速矢量分布截然不同。以432，433，434和435点为例，孔隙水流速分别为：6.66×10−11，5.21×10−11，4.63×10−11，4.58×10−11m/s(工况 1)；5.43×10−9，5.07×10−9，4.85×10−9，4.72×10−9(工况 2)。可见工况2的流速比工况1约大2个数量级。

图14 岩体中2个点的孔隙水压力−时间曲线Fig. 14 Pore pressures versus time at two nodes for two cases

图15 两种工况下4 a时岩体中的孔隙水压力等值线(单位：MPa)Fig. 15 Contours of pore pressures in rock mass at four years for two cases

图16 4 a时计算域中的孔隙水流速矢量Fig. 16 Flow vectors of poree water in calculation domain at four years for two cases

图17 4 a时计算域中正应力等值线(单位：MPa)Fig. 17 Normal stress contours in calculation domain at four years

图17 所示为4 a时计算域中正应力等值线。从图17可见：2种工况的计算域中应力量值及分布也差别很大，如到4 a时，432，433，434和435各点水平正应力/垂直正应力依次为：−9.9/−31.6 MPa，−12.5/−33.4 MPa，−14.2/−34.8 MPa 和−15.5/−35.9 MPa(工况 1)；−19.0/−41.3 MPa，−20.7/−42.9 MPa，−20.8/−43.6 MPa和−20.5/−43.7 MPa(工况 2)。其原因在于与工况 1相比，工况2中孔隙水的压力较小但其流速较大，由此产生的动、静水压力更显著地扰动了岩体应力。

4 结论

(1) 将 Taron等建立的颗粒聚集体的压力溶解模型引入孔隙介质热−水−应力耦合有限元程序中，以一个假定的实验室尺度且位于饱和颗粒聚集体孔隙岩体中的高放废物地质处置模型为例子，就考虑边界上孔隙水压力相等与否的两种工况，通过热−水−应力耦合的二维有限元模拟，考察了岩体中的温度、颗粒界面及孔隙中的溶质浓度、迁移和沉淀量、孔隙率及渗透系数、孔隙水压力、地下水流速和主应力的变化、分布情况。

(2) 2种工况中的温度状态基本相同，计算终了4 a时，近场的温度可达到 40.0～98.0 ℃；相比于工况 1的相同孔隙水压力边界条件，工况2因其计算域左、右边界存在2.295 MPa 的孔隙水压力差，岩体中有较大的流速(稳态流量Qss)，促进颗粒介质的溶解、迁移和沉淀，使得孔隙率和渗透系数加快下降，从而对渗流场(孔隙水的压力及流速)和应力场产生显著的影响。

[1]Yasuhara H, Elsworth D, Polak A. A mechanistic model for compaction of granular aggregates moderated by pressure solution[J]. J Geophys Res, 2003, Vol, 108, NO. B11, 2530.doi:10. 1029/2003JB002536.

[2]Tenthorey E, Cox S, Todd H. Evolution of strength recovery and permeability during fluid-rock reaction in experimental fault zones[J]. Earth and Plane Sci Lett, 2003, 206: 161−172.

[3]Moore E, Lockner A, Byerlee D. Reduction of permeability in granite at elevated temperatures[J]. Science 265, 1994:1558−1561.

[4]Lin W, Roberts J, Glassley W, et al. Fracture and matrix permeability at elevated temperatures[R]. Workshop on significant issures and available data, near-field/altered-zone coupled effects expert elicitation project. San Francisco, 1997,Novermber.

[5]Polak A, Elsworth D, Yasuhara H, et al. Permeability reduction of a natural fracture under net dissolution by hydrothermal fluids[J]. Geophys Res Lett, 2003, 30(20), 2020. doi:10.1029/2003GL017575.

[6]Durham W, Bourcier W, Burton E. Direct observation of reactive flow in a single fracture[J]. Water Resour Res, 2001, 37:1−12.

[7]Yasuhara H, Elsworth D. Evolution of permeability in a natural fracture: Significant role of pressure solution[J]. J Geophys Res,2004, 109, B03204. doi:10.1029/2003JB002663.

[8]Taron J, Elsworth D. Thermal-hydrologic-mechanical-chemical processes in the evolution of engineered geothermal reservoirs[J].Int J Rock Mech Min Sci, 2009. doi:1016/j.ijrmms.2009.01.007.

[9]Taron J, Elsworth D. Coupled mechanical and chemical processe s in engineered geothermal reservoirs with dynamic permeability[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47: 1339−1348.

[10]Taron J, Elsworth D. Constraints on compaction rate and equilibrium in the pressure solution creep of quartz aggregates and fractures: Controls of aqueous concentration[J].Journal of Geophysical Research, 2010: Vol, 115:B07211.doi:10. 1029/2009JB007118.

[11]Lee D, Elsworth D ,Yasuhara H, et al. Experiment and modeling to evaluate the effects of proppant-pack diagenesis on fracture treatments[J]. Journal of Petroleum Science and Engineering,2006, 74: 67−76.

[12]张玉军. 废料地质处置近场热−水−应力−迁移耦合二维有限元分析[J]. 岩土工程学报, 2007, 29(10): 1553−1557.ZHANG Yujun. 2D FEM analysis for coupled thermo-hydro-mechanical-migratory process in near field of geological disposal of nuclear waste[J]. Chinese Jounal of Geotechnical Engineering, 2007, 29(10): 1553−1557.

[13]Chijimatsu M, Kurikami H, Ito A, et al. Implication of THM coupling on the near-field of a nuclear waste repository in a homogeneous rock mass[R]. DECOVALES III-Task3-Bench Mark Test 1(BMT1)-Subtask BMT1-B, 2002: 1−43.

[14]Rutqvist J, Chijimatsu M, Jing L, et al. A numerical study of THM effects on the near-field safety of a hypothetical nuclear waste repository—BMT1 of the DECOVALEX III project. Part 3: Effects of THM coupling in sparsely fractured rocks[J].International Journal of Rock Mechanics and Mining Sciences,2005, 42(5/6): 745−755.