山奈素与牛血清蛋白相互作用:Tachiya模型与Stern－Volmer方程的对比研究

陶慧林，黎舒怀，徐铭泽，周素莲，刘帅涛，易忠胜

(桂林理工大学 化学与生物工程学院，广西 桂林 541004)

随着光谱技术的不断发展，以灵敏度高、信号稳定为特征的荧光光谱法已成为研究药物及其他小分子物质与蛋白质间相互作用的重要手段［1－3］。山奈素(Kaempferide，KF)化学名为4-甲氧基-3，5，7-三羟基黄酮(见图1)，是一种广泛分布在高等植物中的黄酮类化合物，具有祛痰、防治咳嗽和哮喘、降低血压、降血脂、抗动脉硬化等多种生物功能［4］。在肿瘤临床治疗的应用上，KF与化疗药物的联合应用可起到协同增效的抗肿瘤作用，可望成为有效的抗癌防癌的治疗及保健制剂［5］。目前对于KF与牛血清蛋白(BSA)相互作用的研究主要集中在单纯的荧光光谱法和紫外可见吸收光谱法［6－7］，得到的信息有限，不能满足进一步研究的需要。

本实验利用荧光光谱和紫外可见吸收光谱法，首次采用Tachiya模型与Stern－Volmer方程比较研究了生理条件下KF与BSA之间的相互作用，对二者相互作用的模式、作用力类型以及热力学性质等方面作出阐释。为阐明药物与白蛋白的作用机制，了解药物在生命体内的存储和运输情况，进一步研究天然黄酮类化合物在生物体内的作用提供了重要信息。

图1 山奈素的分子结构式Fig.1 Molecular structure of kaempferide

1 实验部分

1.1 仪器与试剂

RF-5301PC荧光光度计(日本岛津);Carry-50型紫外－可见吸收光谱分光光度计(美国瓦里安);EL204电子分析天平;PT-10便携式pH计。

山奈素(生化试剂，99.0%):用无水乙醇配制成3.494×10－3mol/L储备溶液，使用时移取适量储备溶液，用二次水稀释至1.0×10－4mol·L－1;牛血清白蛋白(BSA，国药集团化学试剂有限公司):用 pH 7.4 的 Tris－HCl缓冲溶液(含 0.10 mol·L－1NaCl以维持离子强度)配制 1.0 ×10－5mol·L－1的BSA储备溶液，于4℃以下保存备用。其它试剂均为分析纯，实验用水为二次蒸馏水。

1.2 实验方法

在10 mL比色管中准确移入1.00 mL 1.0×10－5mol·L－1BSA溶液，用微量注射器依次加入不同量的KF溶液，用pH 7.4的Tris－HCl缓冲溶液定容至10 mL。在设定温度(298、304、310 K)下于恒温水浴中静置5 min。设定激发光栅和发射光栅的狭缝宽度为3.0 nm/5.0 nm，激发波长为280 nm，恒温扫描BSA在290～500 nm的荧光发射光谱。分别固定Δλ=15 nm及Δλ=60 nm，记录KF与BSA混合溶液的同步荧光光谱。测定物质的量浓度比为1∶1的KF与BSA溶液的紫外吸收光谱及荧光发射光谱。

图2 298 K时KF对BSA的荧光猝灭图Fig.2 Fluorescence quenching spectra of BSA in the presence of KF at 298 K

2 结果与讨论

2.1 应用Stern－Volmer方程研究KF与BSA相互作用

2.1.1 KF对BSA的荧光猝灭光谱 将BSA的浓度固定，逐渐增大KF溶液的浓度，荧光猝灭图如图2所示。BSA分子中含有色氨酸、酪氨酸等氨基酸残基使其具有内源性荧光，在348 nm处有最大荧光峰。随着KF浓度的增加，BSA的荧光强度明显降低，这表明KF和BSA之间发生了结合作用。此外，BSA的最大发射波长出现蓝移，表明随着KF浓度的增大BSA发色团的疏水环境发生了改变。

2.1.2 KF对BSA荧光猝灭机理及猝灭常数的确定

通过Stern－Volmer方程［8］分析荧光猝灭数据:

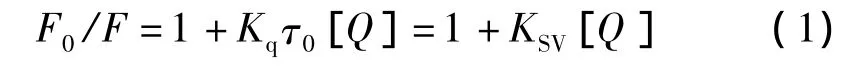
式中:Kq为双分子猝灭过程速率常数，KSV为动态猝灭常数，τ0为无猝灭剂存在下荧光分子的平均寿命，生物大分子的荧光寿命约为10－8s，F0和F分别为未加入和加入KF时BSA的荧光强度，［Q］为猝灭剂KF的浓度。KF和BSA之间相互作用的Stern－Volmer猝灭常数KSV及相关系数r计算结果见表1。

表1 不同温度下KF与BSA相互作用的Stern－Volmer猝灭常数Table 1 Stern－Volmer constant of interaction between KF and BSA at different temperatures

图3 不同温度下KF对BSA荧光猝灭的双对数曲线Fig.3 The double logarithmic curves for the quenching of BSA fluorescence by KF at different temperatures

对于动态猝灭，各类猝灭剂对生物大分子的最大动态猝灭速率常数约为 2 ×1010L·mol－1·s－1［9］。此外，动态和静态猝灭可根据猝灭常数KSV随温度的变化关系加以判断。对于静态猝灭，KSV值随着温度升高而降低，而对于动态猝灭，温度的升高将增加有效碰撞和加剧电子转移过程，使荧光猝灭常数随温度升高而增大［10］。结果表明该反应的 Kq值大于2.0×1010L·mol－1·s－1，且 KSV的值随着温度升高而降低，表明猝灭是静态猝灭，反应形成了BSA－KF基态复合体。

2.1.3 结合常数及结合位点数 当小分子与大分子结合时，其结合常数与结合位点数可从下式获得［11］:

式中n为结合位点数，Ka为表观结合常数，由上式作lg(F0/F－1)～lg［Q］图(见图3)。图中直线的斜率即结合位点数n，截距即lgKa，依直线的斜率和截距即可求出KF与BSA相互作用的结合常数Ka及结合位点数n(见表2)。结果表明，KF和BSA之间存在强大的结合力，并且结合常数Ka随着温度升高而增大，这表明升高温度后KF与BSA的结合能力增强，从而导致BSA－KF复合体的稳定性增大。n值接近于1，表明KF与BSA具有一个结合位点。

表2 通过Stern－Volmer方程得到的KF与BSA相互作用的结合常数Table 2 Binding parameters obtained from the interaction of KF with BSA by Stern－Volmer equation

2.1.4 荧光给体－受体间距离的求取 根据F rster偶极－偶极非辐射能量转移理论［12］，发生能量转移时，非辐射能量转移效率E、供能体与受体之间的结合距离r及临界能量转移距离R0之间有下列关系:

式中K2=2/3;R0是E=50%时的临界距离;N为介质折射常数，取水和有机物折射指数的平均值1.336;Φ为血清白蛋白的荧光量子产率，通常取蛋白质中色氨酸的量子产率0.15［13］;J为给体荧光发射光谱与受体吸收光谱的重叠积分。图4为298 K(A)、304 K(B)、310 K(C)温度下，BSA的荧光光谱与KF的紫外吸收光谱的重叠图谱。

图4 BSA荧光光谱与KF吸收光谱的重叠图Fig.4 Overlap spectra of BSA's fluorescence emission spectra(1)and kaempferide's UV absorption spectra(2)temperature(A－C):298，304，310 K;cBSA=cKF=1.0×10－5mol·L－1

由式(3)～(6)分别求得不同温度下的能量转移效率E、KF在BSA上的结合位点以及蛋白质分子中的214位色氨酸残基的距离r，结果如表3所示。由结果可知，KF在BSA上的结合位点与蛋白质分子中的色氨酸残基Trp 214的距离r＜7 nm，具备了能量转移猝灭蛋白质荧光的条件，因此非辐射能量转移也是引起荧光猝灭的原因之一。另外，在温度为298、304 K时，由于结合距离r小于能量转移效率为50%时的临界距离R0，说明非辐射能量转移引起蛋白质荧光峰猝灭的几率比静态猝灭大，因此非辐射能量转移是KF引起BSA荧光猝灭的主要原因。随着温度升高，能量转移效率为50%时的临界距离R0与结合距离r均逐渐增大，并在310 K时，能量转移效率为50%时的临界距离R0约等于药物与蛋白质的结合距离，因此推测人体生理温度下，非辐射能量转移与静态猝灭共同导致了BSA的荧光猝灭。

表3 BSA荧光光谱与KF吸收光谱重叠积分J与结合距离rTable 3 The overlap integral and binding distances between fluorescence spectra of BSA and absorption spectra of KF

2.2 利用Tachiya模型研究山奈素与蛋白质相互作用

2.2.1 Tachiya模型［14－15］分子与蛋白质之间的吸附与解吸可用下式表示:

式中，Qaq表示猝灭剂分子，Bn表示带n个猝灭剂的BSA。如果BSA中结合位点为m，假设式(7)中的速率常数是合理的:

式中，nav是生物分子中结合的猝灭剂的平均数目，可以通过下式计算得到nav:

在式(12)和式(13)中消去［Qaq］，可以得到:

从BSA到猝灭剂的F rster能量转移速率常数为:

τ0为没有猝灭剂存在时BSA的荧光寿命，r是BSA与猝灭剂之间的距离，R0是F rster非辐射能量转移距离。如果生物分子在与BSA有相同距离r处有n个结合的猝灭位点，荧光强度会变为:

在有无猝灭剂存在的情况下，二者猝灭强度的比值为:

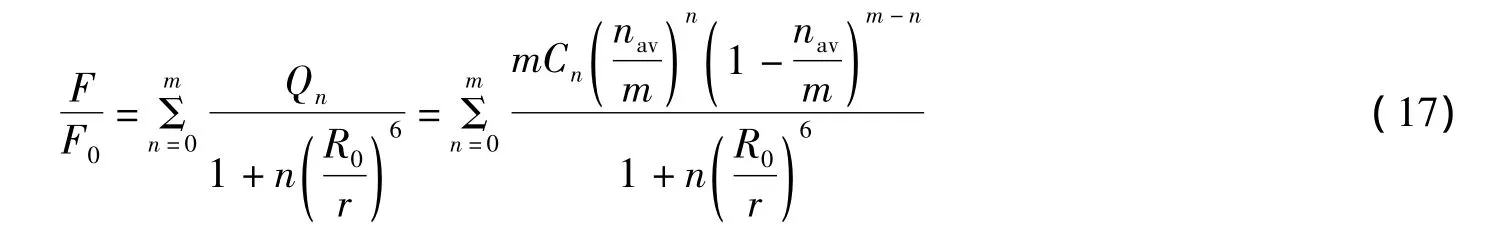
nav可由式(14)求出。通过实验可以获知［M］、［Q］和F/F0的值，结合式(17)和(14)，可以计算出未知变量m、K和r的值，它们均由方程(17)所拟合出的F/F0～［Q］＆［M］曲线所决定。对固定的［M］值，F/F0会随［Q］值增大而减小。然而［Q］值足够大时，F/F0会饱和。因为当所有BSA的结合位点都被猝灭剂占去后，继续增大［Q］不再使结合的猝灭剂数目增加。饱和时猝灭剂结合的数目如下:

因此饱和时的荧光强可以表示为:

另外，［Q］足够小时生物的平均猝灭结合数目也很小，可结合式(14)计算得到:

情况 3.2 {1,2,3}不是X中顶点色集合,以下仅考虑31≤n≤34时的情况,此时C中至多有3个集合不是X和Y中顶点色集合。

此种情况下猝灭结合数目的分布约等于:

从而得出荧光强度为:

此处nav可由式(20)得到。

2.2.2 结合常数与结合距离的求取 通过式(22)可知，当［Q］足够低时，F/F0与［Q］成比例，且比例系数由K、r和［M］决定。因此K、r的值可以由测量两个不同［M］值时的F/F0～［Q］曲线来确定。不同温度下的F/F0～［Q］曲线如图5所示。

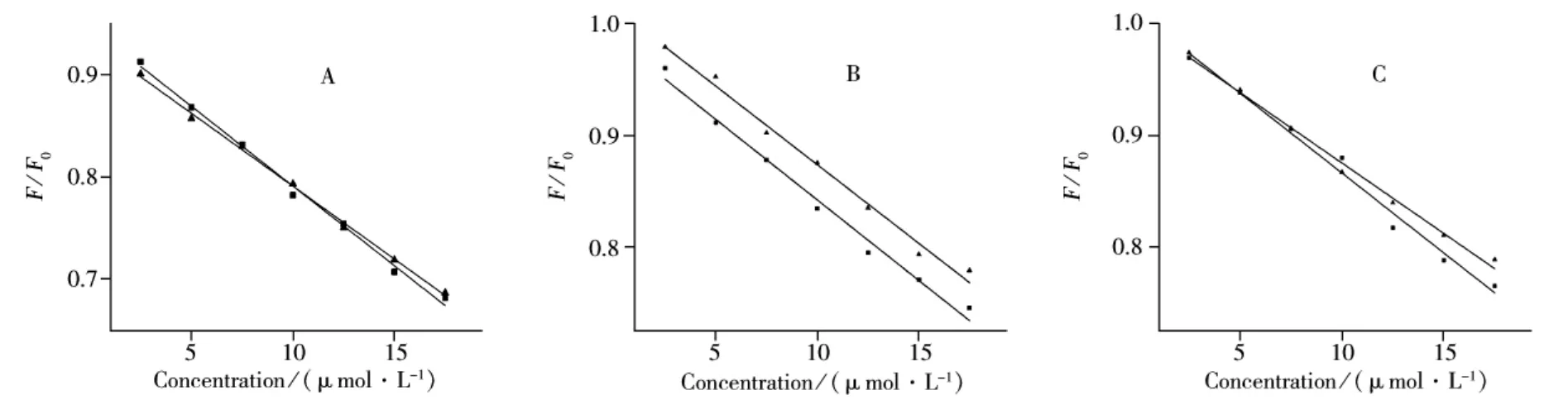
图5 不同温度时的F/F0～KF浓度关系图Fig.5 Curves of F/F0versus concentration of KF obtained by the Tachiya model at different temperatures A.298 K，B.304 K，C.310 K;cBSA: .10 μmol·L －1， .5 μmol·L －1

由式(22)可得BSA与KF相互作用的结合常数K如表4所示，结合常数K随温度的增加而增大，这种趋势与Stern－Volme方程得到的结果一致。但由Stern－Volme方程得到的结合位点数几乎不随温度变化而变化，而由Tachiya模型得到的实际结合位点数却随温度的变化而变化很大。这主要是由于Tachiya模型将结合位点数m与分子实际结合位点数n进行了区别考虑，而Stern－Volmer方程是假定结合位点数即是药物分子实际结合在蛋白质上的数量，这可能并不符合实际情况。Tachiya模型得到的结果更符合小分子与生物大分子相互作用的实际情况。

表4 通过Tachiya模型得到KF－BSA相互作用的结合参数Table 4 The binding parameters of KF－BSA system by Tachiya model

另外，由Tachiya模型得到的结合距离r与Stern－Volmer方程计算的结果亦有较大区别。但两种方法计算出的结合距离r均在2～7 nm范围内，表明由药物向BSA发生能量转移的几率较大，具备了能量转移猝灭蛋白质荧光的条件，因此非辐射能量转移是引起荧光猝灭的原因之一。

2.2.3 热力学参数及作用力类型的求取 小分子和生物大分子之间的相互作用力包括氢键、静电作用、范德华力、疏水力4种［16］。假设在测定温度范围内焓变变化不大，则焓变和熵变ΔS可以从Van t Hoff方程求得:

K近似于在相应温度下Stern－Volmer方程中相互作用体系的结合常数Ka，通过lnK对1/T作图可以得到方程式:lnK=－21 635/T+84.870，r=0.998 6。根据该公式计算得到ΔH和ΔS，再由ΔG=－RTlnK计算ΔG，结果如表5所示。

Ross等［16］根据大量的实验结果，总结出生物大分子与有机小分子等结合力性质与结合作用热力学函数之间的关系，根据反应前后热力学焓变ΔH和熵变ΔS的相对大小，可以判断药物与蛋白质之间的主要作用力类型:ΔH＞0，ΔS＞0为疏水作用力;ΔH＜0，ΔS＜0为氢键和范德华力;ΔH≈0，ΔS＞0为静电引力。由表5可知，该反应是自发反应(ΔG ＜0);ΔH＞0，ΔS＞0，说明KF与BSA之间的作用力为疏水作用力。

表5 KF－BSA相互作用的热力学常数Table 5 The thermodynamic parameters of KF－BSA interaction

2.3 KF对BSA构象的影响

蛋白质的同步荧光光谱常被用来判断蛋白质的构象变化。对于蛋白质的同步荧光光谱，Δλ=15 nm时只表现出酪氨酸残基的荧光，Δλ=60 nm时仅表现出色氨酸残基的荧光。因为氨基酸残基的最大荧光与其所处环境的疏水性有关，所以由荧光波长的改变可判断蛋白质构象的变化［17］。本实验固定激发波长和发射波长的间距为Δλ，同步扫描KF与BSA体系的同步扫描光谱以考察BSA的构象变化(图6)。

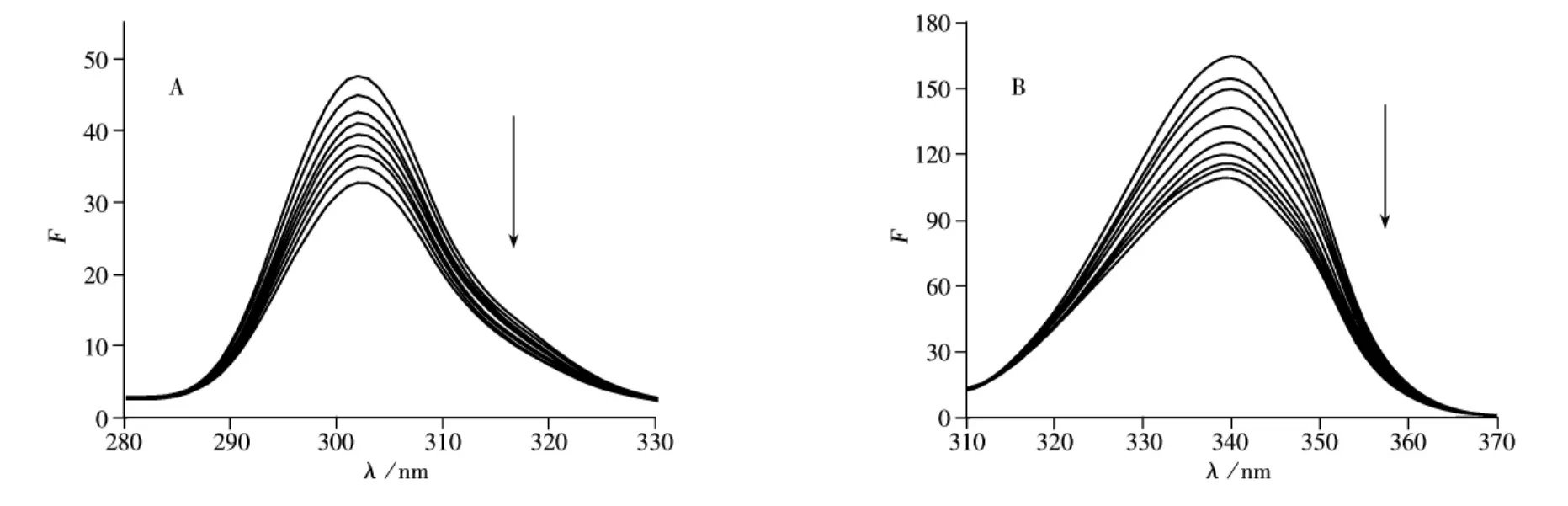
图6 KF与BSA相互作用的同步荧光光谱Fig.6 Synchronous fluorescence spectra of interaction of KF with BSA A.Δλ =15 nm，B.Δλ =60 nm;cBSA=1.0×10－6mol·L－1;cKF=0.0－3.0(×10－6mol·L－1)

由图6可观察到，固定蛋白质浓度，随着KF浓度的增加，BSA分子中酪氨酸残基和色氨酸残基的荧光均被猝灭。KF使BSA的酪氨酸特征荧光峰发生了微弱的红移，表明该残基所处环境的疏水性减弱;色氨酸特征荧光峰发生了微弱的紫移，表明该残基所处环境的疏水性有所增加，蛋白质变得紧密［18］。KF的加入使BSA的构象发生了变化，推测KF与BSA的相互作用可能是通过与色氨酸残基的结合而实现的。

3 结论

利用荧光光谱与紫外可见吸收光谱研究了不同温度下，KF与BSA之间的相互作用。使用Tachiya模型与Stern－Volmer方程，探讨了两种不同数学模型对相互作用体系计算结果的影响。结果表明，使用Tachiya模型时，结合常数Ka随温度的增加而增大，这种趋势与Stern－Volmer方程得到的表观结合常数的变化趋势一致。但由Stern－Volmer方程得到的结合位点数几乎不随着温度变化而变化，而由Tachiya模型获得的实际结合位点数随温度的变化而发生明显变化。Tachiya模型得到的结果更符合小分子与生物大分子相互作用的实际情况。热力学数据表明KF与BSA之间主要依靠疏水作用力结合。同时同步荧光光谱发现KF与BSA的作用可能是通过与色氨酸残基的结合而实现的。

［1］Yu Y M，Feng J C，Liu Y.Acta Chim.Sin.(余燕敏，冯金朝，刘颖.化学学报)，2011，69(2):190－198.

［2］Li C X，Liu S P，Liu Z F，Hu X L.Acta Chim.Sin.(李翠侠，刘绍璞，刘忠芳，胡小莉.化学学报)，2011，69(12):1408－1414.

［3］Zhang X，Kou Z N，Shi Y J，Zhu J B.J.Instrum.Anal.(张曦，寇自农，石羽佳，朱靖博.分析测试学报)，2011，30(4):444－447.

［4］Chang X Q ，Ding L X.Handbook of Analysis of Active Constituents of Chinese Material Medicine.Beijing:Xueyuan A-cademy Press(常新全，丁丽霞.中药活性成分分析手册.北京:学苑出版社)，2002:218.

［5］N r J E，Christensen J，Liu J，Peters M，Mooney D J，Strieter R M，Polverini P J.Cancer Res.，2001，61(5):2183－2188.

［6］Tian J M，Liu J Q，Tian X N，Hu Z D，Chen X G.J.Mol.Struct.，2004，691(1/3):197－202.

［7］Shi J，Cao H.Rev.Bras.Farmacogn.，2011，21(4):594 －600.

［8］Lakowicz J R，Masters B R.J.Biomed.Opt.，2008，13(2):029901 －029902.

［9］Xu J G，Wang Z B.Fluorescence Analytical Methods.Beijing:Science Press(徐金钩，王尊本.荧光分析法.北京:科学出版社)，2006:65.

［10］Yang P，Gao F.The Principles of Bioinorganic Chemistry.Beijing:Science Press(杨频，高飞.生物无机化学原理.北京:科学出版社)，2002:331.

［11］Zhao H W，Ge M，Zhang Z X，Wang W F，Wu G Z.Spectrochim.Acta Part A，2006，65(3):811－817.

［12］F rster T.Ann Physik，1948，2:55 －75.

［13］Feng X Z，Bai C L.Chin.J.Anal.Chem.(冯喜增，白春礼.分析化学)，1998，26(2):154－157.

［14］Xiao J B，Chen X Q，Jiang X Y，Hilczer M，Tachiya M.J.Fluoresc.，2008，18(3):671－678.

［15］Tachiya M.J.Chem.Phys.，1982，76:340.

［16］Ross P D，Subramanian S.Biochemistry，1981，20(11):3096－3102.

［17］Hu Y J，Liu Y，Wang H B，Xiao X H，Qu S S.J.Pharm.Biomed.Anal.，2004，36(4):915 －919.

［18］Pan Z T，Ma Y，Wang W.Chin.J.Anal.Lab.(潘祖亭，马勇，王巍.分析试验室)，2004，23(1):5－8.