平面波激励传输线模型响应分析

张 涛，陈亚洲

（军械工程学院静电与电磁防护研究所，河北石家庄 050003）

随着科学技术的不断发展，空间电磁环境变得越来越复杂，而现代电子系统无不分布着各种传输线网络，如数据通讯、语音通信和供电线路等，形成了分布式的传输线网络。当传输线网络受到磁干扰源（EMI）电磁场激励时，在传输线上和线路末端的负载阻抗上会产生感应电流和感应电压，影响系统的正常工作，严重时会对电子系统造成永久性损坏。因此，研究传输线网络对空间电磁能量的耦合规律具有重要意义，也是提出防护加固措施的理论依据。电磁拓扑理论在分析此类电磁耦合问题时具有很高的应用 价 值［1－2］；BLT方 程 是 电 磁 拓 扑 理 论 的 基石［3－5］；基于多导体传输线理论的BLT 方程，其主要目的就是求解传输线网络终端负载的响应［6］。因此，研究BLT 方程和场线耦合规律具有重要价值。

1 理论推导

对于电磁干扰问题，一般采用电磁散射理论来分析，但是对于传输线这种相对简单的系统，这种方法比较复杂。在分析实际的场线耦合问题时，主要采用Taylor方法［7］和Agrawal方法［8］，研究已经表明，Taylor模型和Agrawal模型其实是对同一个解的不同描述［9－10］。这里采用Agrawal模型方法来推导两线终端负载响应的表达式，并用BLT 方程的形式表示。Agrawal方法等效电磁场激励传输线模型如图1所示。

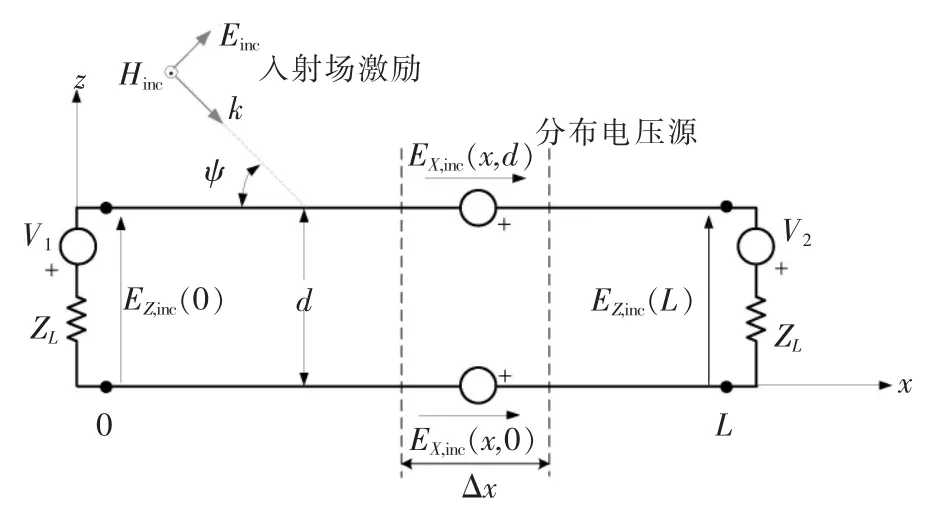
图1 Agrawal方法等效电磁场激励传输线模型Fig.1 Equivalent transimission line mode of Agrawal

对于有限长度为L的传输线，终端负载为Z1和Z2，特性阻抗为Zc的双导线传输线在入射电磁场Einc和Hinc的作用下，通过Agrawal模型推导得到的终端负载响应的电流和电压的BLT 表达式为

当激励源离传输线比较远时，到达传输线处的电磁波就可以认为是平面波，下面就以平面波为激励来分析传输线响应。考虑图2所示的入射平面波情形，场分布由图中的入射角ψ和φ，以及极化角α描述，α定义了电场矢量方向相对于垂直入射面的关系。对于垂直入射极化入射场，电场矢量在入射平面内，α＝0°，对于水平极化入射场，电场垂直于入射面，α＝90°，其中入射电场的幅度为E0。对于这种情况下的激励场，式（3）可以表示为

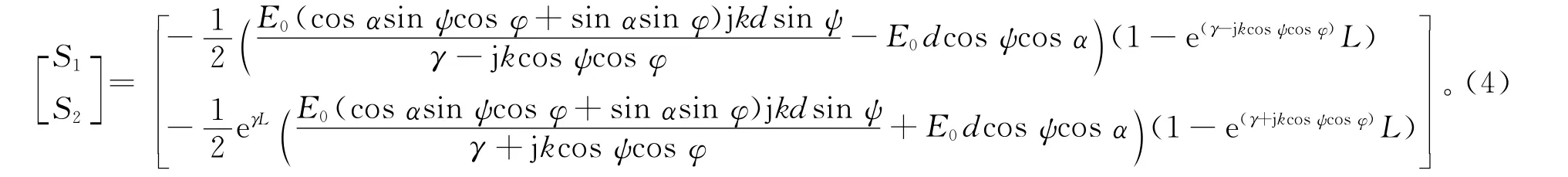
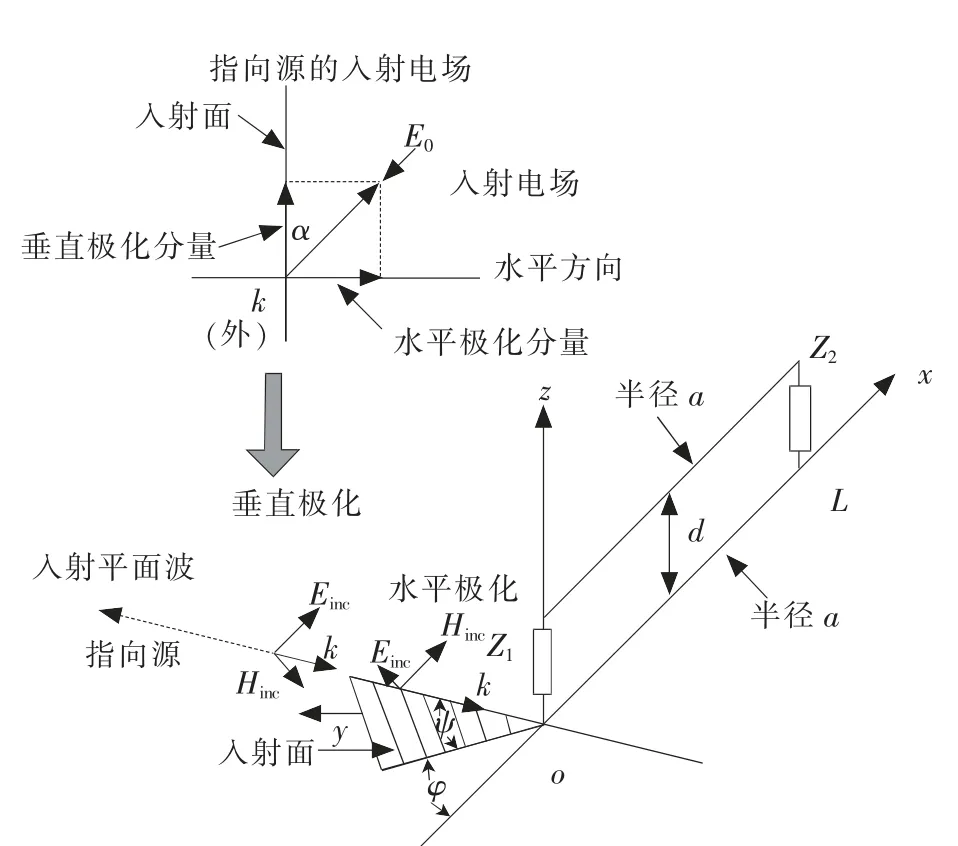
图2 入射平面波激励双线传输线Fig.2 Two conductor transmission－line model excited by Plane Wave

2 仿真分析

改变传输线模型中负载大小、传输线间距、激励源入射角和极化角等参数，分析这些参数变化对传输线终端负载感应电压和电流的影响。

2.1 频域响应

传输线模型的参数设置为线长度L＝30m，导线间距d＝20cm，导线半径a1＝a2＝0.15cm，对于这个特定的几何结构，特性阻抗为Zc＝586Ω，激励源为一个入射角ψ＝60°，φ＝0°的垂直极化波（α＝0°），x＝L处的端接阻抗为Z1＝Z2＝Zc／2＝293Ω，图3给出了x＝L处的流经负载Z2的归一化电流复值频谱的幅值，该电流是依电场幅度E0归一化的，对应单位入射电场的响应。从图中可以看到这个频谱有周期谐振波，这是由于传输线结构对传输线上行波的干扰造成的。

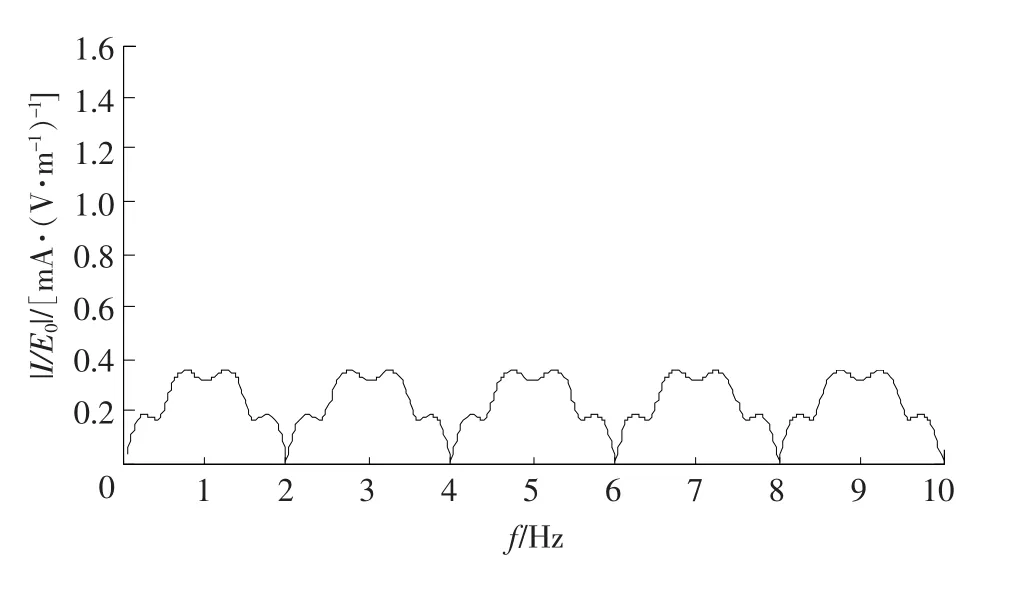
图3 传输线计算x＝L 处负载电流的谱域解Fig.3 Response at x＝Lin frequency domain

2.2 瞬态响应

在理解外部场对传输线耦合机理时，时域响应比频域响应更有用。将BLT 方程给出的频域结果，通过傅里叶变换，可将一个宽带频谱变换到时域。令入射场为一个双指数形的单位幅度垂直极化波，幅度为50kV／m，表达式为

对激励波进行标准的傅里叶变换，将结果与图3所示的响应相乘，在对相乘所得结果进行逆傅里叶变换就可以得到瞬态响应。下面对模型参数变化时响应波形进行分析，总结传输线响应的耦合规律。

2.2.1 终端负载变化时的响应

x＝0端负载取Zc／2＝296Ω，x＝L端负载变化，分别取0，296 Ω 和无穷大，响应波形如图4所示。

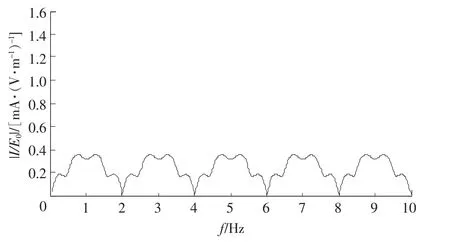
图4 负载变化时的响应波形Fig.4 Response under different load

从图4可以看出，当端接负载为0时，响应幅度最大，负载为无穷大时，响应波形为0，随着端接负载阻值的变大，响应幅度逐渐变小，但波形形状基本不变。由Agrawal模型可知，当导线设置和入射电磁场确定时，感应在导线上的电势已经确定，由欧姆定律可知，改变负载大小能改变感应电流的大小。

2.2.2 线间距变化时的响应

保持其他参数设置不变，仅改变线间距离d，取间距0.1，0.2，0.5，1，2m 进行计算，波形如图5所示，从图中可以看出，当线间距变大时，响应幅度也随之变大，这是因为当线间距离变大时，双线导线间的面积也随着变大，也就是耦合回路面积变大，耦合到传输线的电磁能量也变大的缘故。

2.2.3ψ角变化时的响应

其他参数设置不变，改变入射波ψ角的大小，ψ分别取0，π／6，π／4，π／3，π／2。得到响应如图6所示。从图6中可以看出，当俯仰角ψ取0时，耦合波形幅度最小，两端相差的时间最长。随着俯仰角ψ的逐渐增大，两端相差的时间逐渐减小，当俯仰角ψ为π／2时，两端响应基本没有差别，此时响应到达两端负载的时间相同。

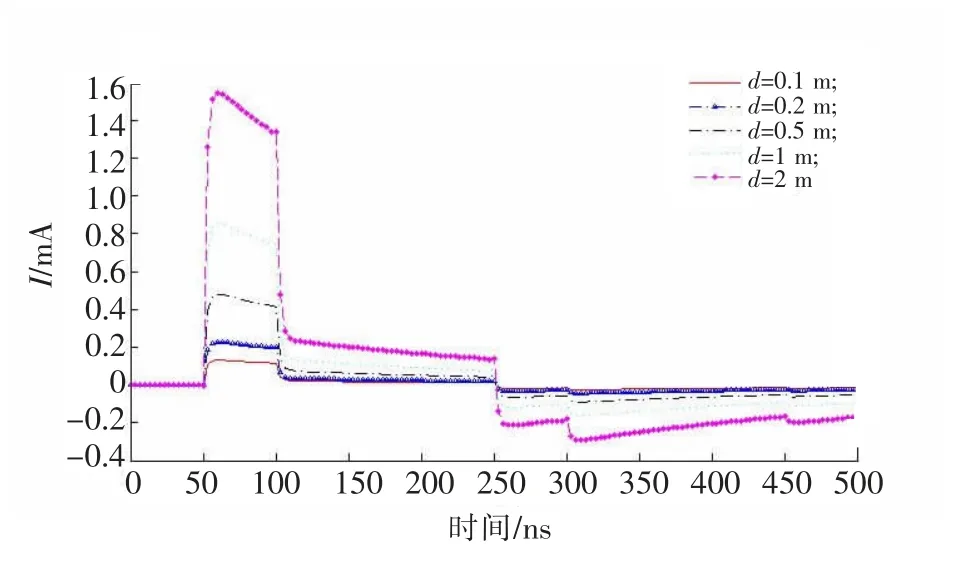
图5 不同线间距响应波形Fig.5 Response under different distance

图6 不同俯仰角ψ 下响应波形Fig.6 Response under different pitch angle

2.2.4 方位角φ变化时的响应

保持其他设置不变，讨论入射波方位角φ变化时响应波形的变化，方位角φ取0，π／6，π／4，π／3，π／2，得到响应如图7所示。可以看出，当方位角φ为0时，响应波形幅度最大，随着方位角φ逐渐变大，响应波形幅度逐渐变小，当φ＝π／2 时，响应波形发生逆转，方向相反。

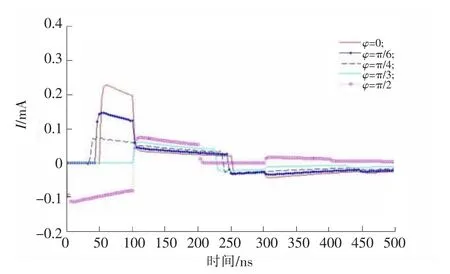
图7 不同方位角φ 下响应波形Fig.7 Response under different azimuth angle

3 结 语

以传输线理论为基础，通过Agrawal模型方法推导了两线终端负载响应的BLT 表达式，并仿真得到不同模型参数条件下平面波激励终端负载的响应波形，得出参数变化对负载响应的影响。线缆耦合是导致电磁干扰问题的主要途径，外部电磁能量会经传输线耦合进入系统内部形成干扰，严重的会损坏系统，因此，对平面波激励下传输线终端负载响应的研究具有十分重要的意义。传输线理论非常适合用于分析线缆耦合这种实际工程问题，因此，本文的分析结果可以用来解决实际系统电缆引起的EMI问题。

／References：

［1］ BAUM C E.Electromagnetic topology：A formal approach to the analysis and desigh of complex electronic systems［A］.Proceedings of the 4th Symposium and Technical Exhibition on EMC［C］.Zurich：［s.n.］，1981.209－214.

［2］ BESNIER P.Electromagnetic topology：An additional interaction sequence diragrm for transmission line network analysis［J］.IEEE Transactions on Electromagnetic Compatibility，2006，48（4）：685－692.

［3］ 李许东，王庆国，周 星，等.基于BLT 方程的传输线网络电磁脉冲响应分析［J］.河北科技大学学报，2011，32（2）：183－186.LI Xudong，WANG Qingguo，ZHOU Xing，et al.Electromagnetic pulse response analysis of the transmission line network based on the BLT equation［J］.Journal of Hebei University of Science and Technology，2011，32（2）：183－186.

［4］ 王宝和.电磁拓扑中BLT 方程的建立及应用研究［D］.北京：国防科技大学，2006.WANG Baohe.Research on Creating and Applying of BLT Equation about Electromagnetic Topology［D］.Beijing：National University of Defense Technology，2006.

［5］ 林竞羽，周东方，毛天鹏，等.电磁拓扑分析中的BLT 方程及其应用［J］.信息工程大学学报，2004，5（2）：118－121.LIN Jingyu，ZHOU Dongfang，MAO Tianpeng，et al.BLT equation in electromagnetic topology analysis and its application［J］.Journal of Information Engineering University，2004，5（2）：118－121.

［6］ BAUM C E，LIU T K，TESCHE F M.On the Analysis of General Multiconductor Transmission－Line Network.Interaction Note 350［M］.New Mexico：Kirtland Air Force Base，1978.

［7］ TAYLOR C D，SATTERWHITE R S，HARRISON C W.The response of a terminated two－wire transmission line excited by a nonuniform electromagnetic field［J］.IEEE Trans Antennas Propag，1987，13（6）：987－989.

［8］ AGRAWAL A K.Transient response of multiconductor transmission lines excited by a nonuniform electromagnetic field［J］.IEEE Trans Electromagn Compat，1980，22（2）：483－487.

［9］ 谢彦召，王赞基，王群书，等.地面附近高架线缆HEMP 响应计算的Agrawal和Taylor模型比较［J］.强激光与粒子束，2005，17（4）：575－580.XIE Yanzhao，WANG Zanji，WANG Qunshu，et al.The ground near overhead cables HEMP response calculated comparison of Agrawal and Taylor models［J］.High Power Laser and Particle Beams，2005，17（4）：575－580.

［10］ 倪谷炎，罗建书，李传胪，等.Taylor与Agrawal传输线耦合模型解的比较［J］.强激光与粒子束，2007，29（5）：111－116.NI Guyan，LUO Jianshu，LI Chuanlu，et al.Comparison of Taylor and Agrawal transmission line coupling model solutions［J］.High Power Laser and Particle Beams，2007，29（5）：111－116.