光纤制造智能调度研究

姜培明，郑永前

（1.同济大学机械工程学院，上海 200092；2.康宁（上海）光纤有限公司，上海 200233）

光导纤维（以下简称光纤）是一种由光在特殊材料制造而成的纤维中按照全反射原理传送的光传导工具，在玻璃核心之外，由化学制涂料作为保护套，使其能够做小于60°弯曲但是不至于断裂。通常光纤的一头发射装置使用发光二极管或者激光将光脉冲传送至光缆，另一端使用光敏元器件检测脉冲。包含大量光纤的线缆称为光缆。由于光在光纤中的传送损失比电在电线中的损耗低很多，更因为主要原材料蕴藏量巨大，易开采，因此价格便宜，此2种因素促使光纤被用作目前最主要的长距离大信息量的信息传送工具［1］。

光纤的制造工艺分为预制棒成型、光纤拉丝、光纤复绕、光纤测试，其核心生产工艺在预制棒成型以及光纤拉丝，这2个站点是典型的工作站并且站内都有大量的相同设备。与大多数规模化生产的工作站型产业类似，多生产线对多生产线调度的问题也是光纤制造调度的一个主要研究问题。多生产线调度问题兼有Parallel－machine（多生产线并行）调度和Flow－shop（流水车间）调度的特点，是一种较新的调度领域研究对象。目前多生产线调度问题的研究还属于起步阶段，主要存在如下问题：

1）将多生产线的并行生产等同于多台机器的并行生产方式；

2）将调度问题中的各条生产线当作同样功能、效率及质量的设备来处理；

3）分批策略制定不合理，批次是固定的而不是动态的；

4）多生产线调度问题研究多数为单目标的调度研究［2］。

解决多生产线多目标智能调度目标在于迅速为生产物料寻找到合适的匹配机器。光纤制造高速度生产及长准备时间的生产特点决定了光纤生产前道拉丝不可能因为质量缺陷而停机重启动，只能在后道工序进行废弃。因此根据不同的批次大小，最大化系统效率，充分利用瓶颈工序的产能来决定匹配机器是一个有实际意义的研究。本文提出应用于多目标多生产线调度问题更有效的新算法。

1 多生产线多目标调度问题

1.1 多生产线作业协调调度问题

在过去的几十年中，人们对于调度问题进行了大量的研究，主要的方法有应用数学、运筹学、目标规划和动态规划以及决策分析方法等，研究并解决了一系列的有代表意义的调度和优化。20世纪70年代起人们对于各种调度问题的研究不断深入，大量的研究表明调度问题的复杂性超出过去研究的想象，许多调度的问题被证实为NP－Hard问题［3］。

随着计算机技术的发展，利用大数规则及穷举法等为NP－Hard问题的研究带来了契机，另外神经网络、遗传算法、退火算法等智能算法逻辑的发展也为复杂调度问题的解决提供了新的手段［4］。

多生产线调度问题可以简单描述为n个工作如何分配给m台机器的问题，虽然这个问题可以用简单的排列组合方式进行描述，但一般来说会有作业优先级、时间限制、平行移动、不允许停止等制约条件。同时一般的目标均为在最小化的时间内完成指定任务集。

1.2 多目标优化问题及权重选择

在离散制造生产系统中，一个工件一般经过一系列的工艺过程加工完成，每道工序需要特定的机器和其他的资源共同来完成，各个工件在各机器上的加工顺序（称为技术约束条件）通常是事先给定的。车间调度的作用就是根据现有的资源状况合理地安排作业加工顺序，以满足特定生产目标的要求，一般包括作业排序和资源分配，但本文中加入第三因素（Work In Process在制品控制）和第四因素（考虑后续站点的批次数量集中处理），通过现场智能化计算机管理进行更好的逻辑控制。

多目标问题的解决必定会面临各个分解目标的权重研究，本文在对于各种权重方法研究筛选后，确定适合于实际生产问题的变异系数法（Coefficient of Variation method）。该方法直接利用各项指标所包含的信息，通过计算到指标权重，是一种客观赋权的方法。

1.3 多生产线多目标调度实例说明

以下例子中使用的数据均由笔者根据实际情况提取的部分设备作为实验数据（见图1）。

某生产线上的设备Process 1＃内已经完成M台设备上的m个盘（M＝1，2，…，m，（m＝5）），同时有后道对应的Process 2＃N台复绕机（N＝1，2，…，n，（n＝10）），复绕机后有Process 3＃设备烘箱，充入贵重气体对光纤进行处理，满箱才能开启，每满箱长度为800km。初始数据采用现场PLC／SCADA 回馈数据，根据当时现场实际回馈数据得到表1。图1由Length 意义为初始瞬时Process 1＃之后等待的在制品盘长，Left Time意义为Process 2＃上现有的大盘根据盘长与运行速度，系统自动计算的剩下的时间。Length 为Process 2＃上当前运行盘的长度。Process 3＃的Chamber Length（km）代表现有烘箱内的长度。

实际生产中一般用效率为系统整体运行的考量标准，但此工序为工厂的非瓶颈工序，因此不必以传统的OEE 目标来进行衡量，根据TOC 理论（Theory of Constraint）及工厂实际运行经验，将该效率指标分为两个方面即烘箱等待时间，以及后道WIP 移动速度。对上述指标进行量化，定义目标函数如式（1）所示：

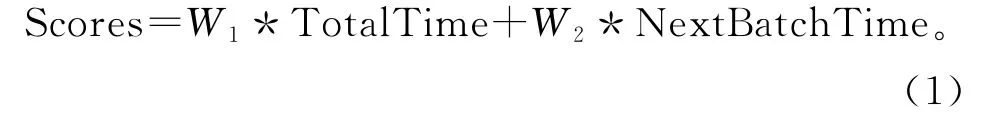
式中：TotalTime为达到批次的最小时间（假设满箱公里数800km），W1＝（权重1）；NextBatch－Time为Process 2＃，Process 3＃内堆积的WIP数量最少，将公里数通过速度转化为时间；W2＝（权重2），其代表着合理地控制在制品、半成品的储备量，本文中适应度函数与目标取相同意义［6］。

图1 现场实际情况模拟图Fig.1 Shop floor situation chart

权重的选择采取变异系数法，取30d 现场数据，将每天产量作为评价指标。通过Minitab 计算，由表1表达计算过程，首先得到30d的现场数据的均值和标准差，在此对于考量的2个变量进行一定的说明便于读者的了解。TotalTime 相当于Process 3＃的等待总时间，即从开箱后（箱内公里数为0）开始到满箱（箱内公里数为800km）的时间；NextBatchTime为一个设计的考量后道WIP 移动速度的概念，相当于throughput，根据李特尔定律（Little’s Law）WIP＝Throughput×Cycle Time的变化，本文取Next Batch Time＝WIP／Throughput，其表达的含义为后道WIP 整体的在制品移动的速度。即可以等同为烘箱开箱时间的最重要的考量因素。根据实际数据的计算CV＝σ／μ得到Coefficient of Variance（变异系数），通过比例变化为权重的对应值。

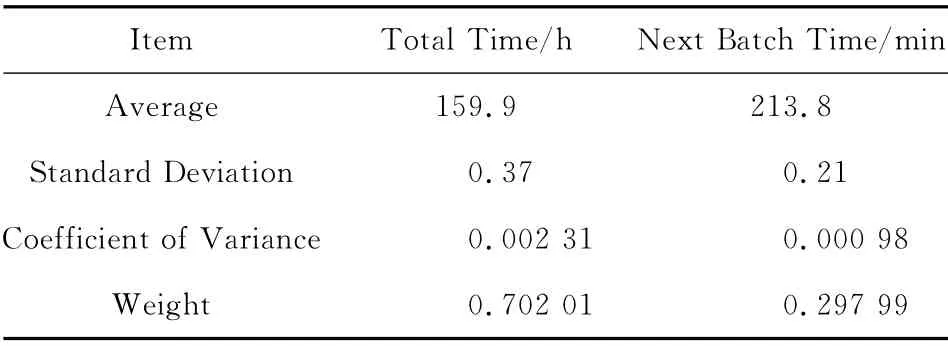
表1 变异系数法计算关键数值表Tab.1 Critical data sheet of coefficient of variance calculation

1.4 遗传算法简介及算法流程图

遗传算法是计算数学中用于解决最优化的搜索算法，是进化算法的一种。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的，这些现象包括遗传、突变、自然选择以及杂交等。

遗传算法通常实现方式为一种计算机模拟。如图2所示描述了最基本的遗传算法的流程图，对于一个最优化问题，可以表述为一定数量的候选解（称为个体）的抽象表示（称为染色体）的种群向更好的解进化。传统上，解用二进制表示（即0和1的串），但也可以用其他表示方法。进化从完全随机个体的种群开始，之后一代一代发生。在每一代中，整个种群的适应度被评价，从当前种群中随机地选择多个个体（基于它们的适应度），通过自然选择和突变产生新的生命种群，该种群在算法的下一次迭代中成为当前种群。

经过这一系列的过程（选择、交配和突变），产生的新一代个体不同于初始的一代，并一代一代向增加整体适应度的方向发展，因为最好的个体总是更多的被选择去产生下一代，而适应度低的个体逐渐被淘汰掉。这样的过程不断的重复：每个个体被评价，计算出适应度，2个个体交配，然后突变，产生第3代。周而复始，直到终止条件满足为止，即种群进化到一定的收敛时期，通过优胜劣汰，最后留下的种群还原编码即为最优解集［7］。

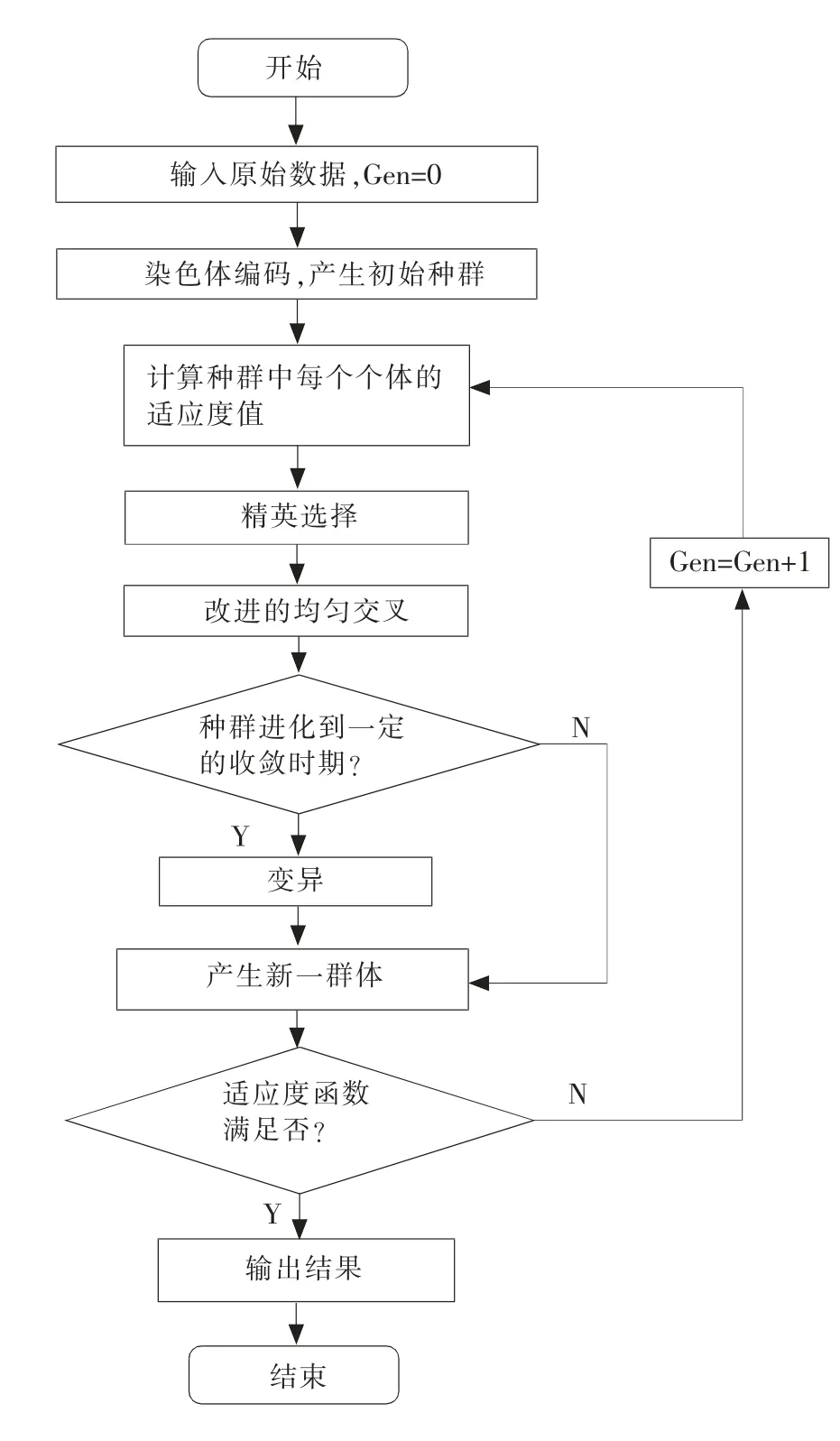
图2 遗传算法基本流程图Fig.2 Genetic algorithm process chart

2 应用实例

2.1 遗传算法部分程序及参数设置

2.1.1 遗传算法主要参数设置

首先作者要确定的是初始种群数量（Population size）和变量数（Number of Variable），种群数量是本代对应的基因数量，例如选择种群数量为100，在适应度函数内的变量数为3的话，代表了本代有［100，3］的矩阵，同一个个体只能在种群中产生一次。根据本例适应度函数确定变量数为5，对应5个输入盘。

随后设定的是交叉概率（Crossover fraction）此参数对应的是当前代后一代对应的变异概率，参数为［0，1］中的任意数。从0到1对应交叉概率从大到小，0代表者完全变异子代，1 代表所有的子代除了精英个体外都是交叉子代，作者根据文献［14］选择0.8作为合适的交叉概率。

接着进行选择操作，尺度函数（Scaling function）其代表编码过程选择的方法，本文选择的是按比例计算又称为选择的蒙特卡罗法，即利用比例于各个个体适应度的概率决定其子孙的遗留可能性。

分子fi是单个适应度函数值，分母所有适应读函数的值的求和（i＝1，2，…，M）。

变异函数（Mutation function）描述了基因算法怎么对于整个代群体的个体进行随机变化，本文选择了自适应法（Adaptive feasible）。变异选择一个适当的变异率，设平均的适应度函数为f，如果单体的适应度为f1，如果f1＞f那么变异率会变低，相反则变异率变高，保留最优解，但是不好处就是可能会有局部收敛的问题。下面是变异率的公式，公式中Npar是染色体设定的数量，βk是第k个染色体编码的位数，λ为染色体位数。

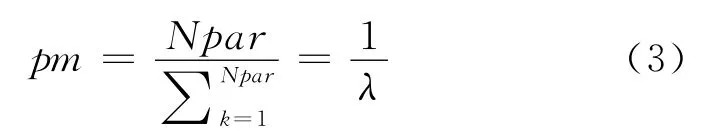
编码方式选择实数编码方式，对应现场工序1产生的5个盘即认为是数列的第1～第5个框，工序2有10台机器可以选择，因此考虑之前选择的种群数目100，由计算机随机生成100个父代种群，例如图3所示数列。

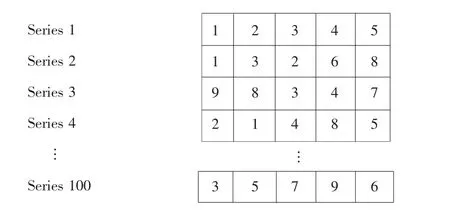
图3 父代种群排列编码Fig.3 Code array of parent generation

作者可以认为每1个数列都是5位，每1位代表前道工序的设备上的盘，以Series 1 为例，可以被解释为第1个盘对应2＃工序第1台设备，第2个盘对应2＃工序第2台设备，依此类推。

2.1.2 程序伪码（自定义遗传算法，适应度函数偏弱）

本程序为伪码，仅仅描述程序主体适应度函数定义，计算过程，限于篇幅遗传算法定义及参数设置程序未列出。

2.2 收敛结果及最优解

图4为从基因代数及适应度函数收敛图，可知整体系统在第48代进入收敛，收敛值415.05 即为本文中公式（1）所述适应度函数的最小值，也是对应系统效率最大的数值。本例对应最优解集为｛3，4，5，1，7｝表达的含义为，1至5号等待的盘分别依次等待现有3号，4号，5号，1号，7号设备上在制盘结束后依次上机。根据结果重新调整生产安排如图5所示，整体效率经过数据符合确实是现有条件的最优解。

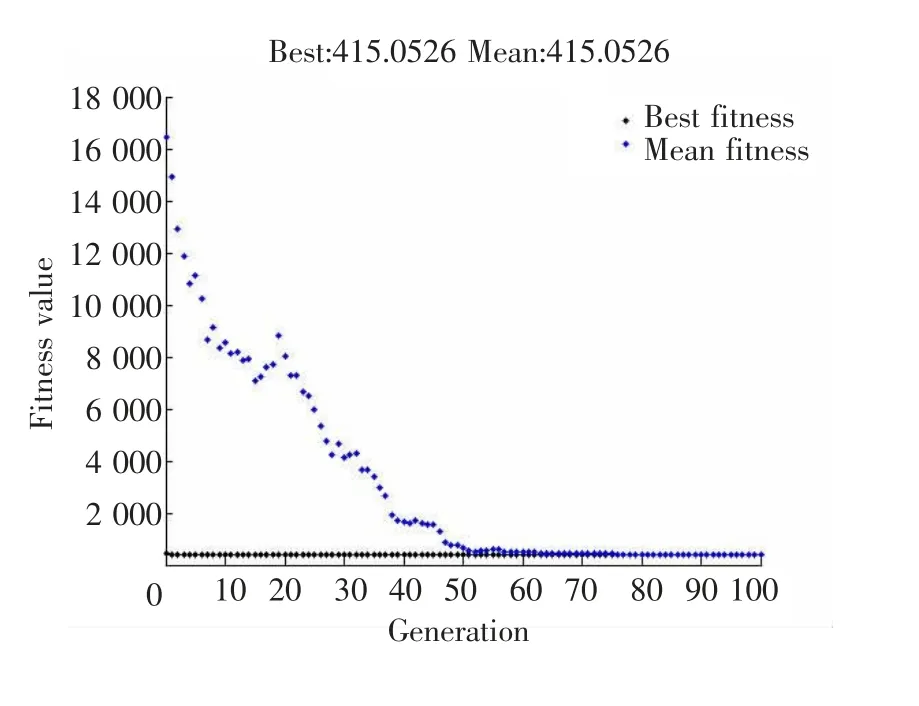
图4 基因代数及适应度函数收敛图Fig.4 Genetic generation and fitness function convergence plot

3 结 语

本文结合遗传算法提出实际生产中调度多目标优化方法，对方法进行了实例验证，证明方法的可行性。其研究意义和新颖性如下。

1）现代大规模集约式生产工厂均为技术密集型或者设备密集型，且流程复杂，通过该种算法可以适用于多目标，更多设备，更复杂的模型，降低生产线管理者的劳动负荷，提高反应速度及生产效率。

2）实际生产过程中管理者作决策时往往有优先级排序及多目标决策等一系列过多依赖于主观判断的考虑因素，通过既定的系统设计可以避免由于人员经验不足造成的错误决策。

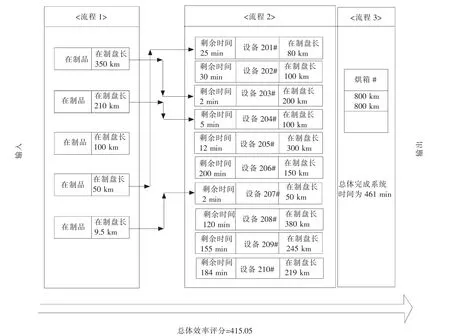
图5 系统盘路径分配图Fig.5 System spool route allocation map

／References：

［1］ HECHT J.Understanding of Fiber Optics［M］.5th ed.New Jersey：Published by Pearson Education，2006.

［2］ PINEDO M.Scheduling：Theory，Algorithms，and Systems［M］.New York：Publisher Springer，2008.

［3］ HOPP W J，SPEARMAN M L.Factory Physics－Foundations of Manufacturing Management［M］.北京：清华大学出版社，2008.HOPP W J，SPEARMAN M L.Factory Physics－Foundations of Manufacturing Management ［M］.Beijing： Tsinghua University Press，2008.

［4］ 孙敬武，牛习现，范秀平，等，基于多Agent的通用智能网络管理系统设计与实现［J］.河北工业科技，2012，29（6）：415－420.SUN Jingwu，NIU Xixian，FAN Xiuping，et al.Design and implementation of multi－Agent－based general intelligent network management system ［J］.Hebei Journal of Industrial Science and Technology，2012，29（6）：415－420.

［5］ GREFENSTETTE J J.Proceedings of the First Conference on Genetic Algorithms and their Applications［M］.New Jersey：Lawrence Erlbaum Associates Inc，1985.

［6］ ISO TC184／SC5N1052，ISO／WD 22400－2，Automation System and Integration－Key Performance Indicators（KPIs）for Manufacturing Operations Management－Part 2：Definitions and Descriptions［S］.

［7］ IEC 62264－3，Industrial－process Measurement and Control Enterprise Control System Integrations－Part 3 ：Activity Models of Manufacturing Operations［S］.

［8］ 张 军，詹志辉，陈 伟，等.计算智能［M］.北京：清华大学出版社，2009.ZHANG Jun，ZHAN Zhihui，CHEN Wei，et al.Computational Intelligence［M］.Beijing：Tsinghua University Press，2009.

［9］ JEFFREY H W.Handbook of Production Scheduling［M］.New York：Springer，2006.

［10］ STECKE K E，MORIN T L.The optimality of balancing workload in certain types of flexible manufacturing systems［J］.Europ J Oper，1985，20：68－82.

［11］ 雷英杰.MATLAB 遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005.LEI Yingjie.MATLAB Genetic Algorithm Tool Box and Application［M］.Xi′an：Xi′an Electronic Science ＆Technology University Press，2005.

［12］ 高鸿斌，张永强，张 佳.基于PLC 自动配料控制系统的设计与实现［J］.河北工业科技，2011，28（3）：167－169.GAO Hongbin，ZHANG Yongqiang，ZHANG Jia.Design and implementation of aggregate and powder burdening system based on PLC［J］.Hebei Journal of Industrial Science and Technology，2011，28（3）：167－169.