基于TOPSIS的铁路应急资源调度优化模型

王东海，段力伟

（1.北京铁路局 调度所，北京 100860；2.西南交通大学 交通运输与物流学院，四川 成都 610031）

1 概述

铁路运输网络中发生应急灾害后，考虑到救援的紧迫性，以及应急资源的调度受到距离和时间的限制，初期所调度的应急资源总量不一定能够满足事故点的全部需求，这样就不可避免地会出现某个事故点的某种应急资源需求得不到满足的情况。因此，对优先权较高的事故点进行优先调度十分必要，从而降低由资源不足带来的损失。

目前，根据事故点的数量与资源类型的不同，可以将应急资源调度问题分为单事故点单资源、单事故点多资源、多事故点多资源的应急资源调度问题[1-9]。其中，提出在事故点优先权不同情况下应急资源调度方案的求解思路，并未给出确定事故点优先权的有效方法和合理的资源调度模型[3]；以运输成本最小为优化目标，构建单事故点多出救点多资源的应急资源调度模型，并将事故点对应急资源需求的紧迫度这一参数加入模型中，提高了应急资源的调度效率，但是并未给出资源需求紧迫度的确定方法[5]；利用 TOPSIS 模型，对不同群组的受灾地点的救援优先权进行计算，并提出了应急救援物资的调配模型，而利用 TOPSIS 模型确定事故点救援优先权的方法，对于确定救援顺序、确保物资合理分配具有很好的借鉴意义[6-8]。

因此，以铁路应急资源调度问题为研究对象，针对地震、洪水、飓风等大规模自然灾害的发生造成路网内出现多处运输事故的情况，给出确定不同事故点优先权的方法，并构建多出救点、多资源的应急资源调度模型，在保证高优先权事故点的应急资源需求满足的前提下，使应急资源调度时间与调度成本、惩罚成本之和最小。

2 事故点优先权的确定方法

铁路网中多个地点同时发生应急事件时，由于事故点所处的线网位置、受影响列车的类型、事故点的破坏程度及人员伤亡/货物损失等情况的不同，事故点之间的救援紧迫度也会有所差异。借助基于熵权的 TOPSIS 评价模型[10-13]，通过设定线路等级、列车等级、灾害程度、线路损毁程度 4个评价指标，计算不同事故点的救援优先权。

（1）设事故点集合 G = { Gj| j = 1，2，…，n }，根据线路等级、列车等级、灾害程度、线路损毁程度 4个指标，确定事故点 Gj的救援优先权的评价指标集合为 Pj= { pkj| j = 1，2，…，n ；k =1，2，…，4}。由此构建的评价指标特征矩阵 P：

（3）定义第 k(k = 1，2，3，4)个指标的熵值为将熵的互补值( 1-ξk) 进行归一化处理后[10-13]，作为第 k个指标的客观权重 φk：

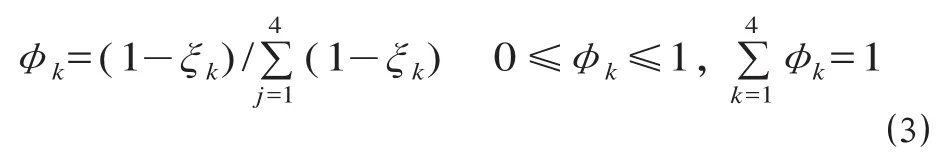
（4）确定理想解 H+与负理想解 H-。其中：

（5）计算事故点 Gj到理想解 H+与负理想解 H-的加权欧几里得距离，距离尺度通过将客观权重φk与欧几里得距离进行加权来计算。定义事故点 Gj到理想解 H+的距离为 D+j，到负理想解 H-的距离为 D-j。即

（6）确定事故点 Gj到理想解的相对贴近度Ej。即

Ej值越大，表示事故点 Gj的优先权越高；Ej值越小，表示事故点 Gj的优先权越低。

3 应急资源调度模型的构建

3.1 符号与变量定义

设出救点集合 C ={Ci| i = 1，2，…，m}，应急资源的种类集合 R ={Rl| l = 1，2，…，q}。相关符号和变量定义如下：dlj为灾害发生后事故点 Gj对 Rl类资源需求量；sli为救援开始后出救点 Ci对 Rl类资源可用量；tij为由出救点 Ci调度到事故点 Gj的最短旅行时间； ρl为 Rl类应急资源的单位调度成本；κl为Rl类应急资源调度不足时的单位惩罚成本；xlij为救援过程中，由出救点 Ci调度到事故点 Gj的 Rl类资源量；其中，i = 1，2，…，m；j = 1，2，…，n；l = 1，2，…，q。

3.2 目标函数与约束条件

在只考虑由灾害导致的直接损失前提下，铁路应急资源调度模型的构建目标，应考虑到救援的紧迫性，以救援时间(称之为“总调度时间”) 最短作为主要考虑因素。同时，还应考虑到资源本身的价值和调配成本(称之为“总调度成本”)，以及由于救援资源不能足量到达事故点而引起的进一步损失( 称之为“总惩罚成本”)。

由于不同优先权的事故点对于资源的需求程度也不同，因此需要将事故点的优先权表示在目标函数中。设αj为事故点 Gj的调度时间及成本系数，βj为事故点 Gj的惩罚成本系数 (j =1，2，…，n)。通过加入该系数，可以将由事故点优先权不同导致的损失后果不同反应在目标函数中。

目标 1：总调度时间 W1为

目标 2：总调度成本 W2为

目标 3：总惩罚成本 W3为

该模型的约束条件主要考虑两点：①事故点 Gj所获得的应急资源总量不能大于其需求量，以免浪费宝贵的救援资源，即：②出救点Ci所输出的应急资源总量不会超过其可用量，即：

3.3 建立模型

根据上述分析，设 θ 为时间成本转换系数，构建铁路应急资源调度优化模型如下。

4 算例分析

4.1 基本条件设定

假定某地区发生地震后，导致某铁路局范围内出现 4 处事故点，事故列车的类型、线路等级均有所不同，且分别造成了一定程度的人员伤亡、货物损失、车辆损毁及线路中断，需从该地区的7个应急资源储备点调集 5种不同的资源，进行事故救援。则有：G = {G1，G2，…，G4}，C = {C1，C2，…，C7}，R = {R1，R2，…，R5}。

根据铁路应急资源的分类[3]，设定此次救援所需的应急资源分别为：救援运输工具 R1(单位：辆，如救援列车、消防车、急救车等)，救援工具及机械 R2(单位：台，如液压剪、检毒设备、起重器械等)，消防设施设备 R3(单位：套，如灭火器、消防给水系统等)，事故救援队 R4(单位：支，如专业救援人员、军队、公安、消防等)，救援医疗器械 R5(单位：套，如急救箱、呼吸器等)。

事故点应急资源需求量如表1 所示，出救点应急资源可用量如表2 所示，不同应急资源的单位调度成本、单位惩罚成本如表3 所示，出救点至事故点的最短旅行时间如表4 所示。

表1 事故点的应急资源需求量

表2 出救点的应急资源可用量

表3 不同类型资源的单位成本

表4 出救点至事故点间的最短旅行时间

4.2 事故点优先权计算

根据事故点的线路等级(p1j)、列车等级(p2j)、灾害程度(p3j)及线路损毁程度(p4j) 4个不同的指标，确定事故点 Gj的评价指标集合 Pj。为便于比较和计算，按照事故点受灾害影响的程度大小不同，通过比较不同事故点损失的严重程度，将上述 4个指标按照非常严重、严重、一般、不严重、无影响5 类，分别对应取值 4、3、2、1、0，则优先权评价的特征矩阵 P 为：

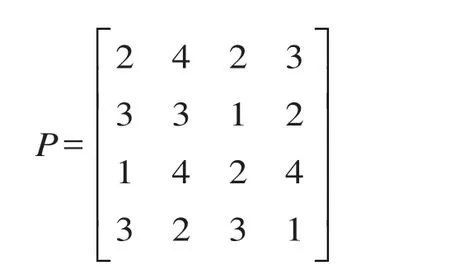
由公式⑶—⑹计算得到：

因此，4个事故点的救援优先权为(2，4，1，3)。

4.3 模型求解与结果分析

根据事故点 Gj的优先权，令时间及成本系数 αj的取值分别为10、0.01、100、0.1。对于 βj，令 β1= β3= 105(即充分大的数)， β2= β4= 1，代表事故点 G1、G3的应急资源需求必须得到满足。

由于铁路应急资源调度优化模型属于线性规划模型，可采用 LINGO 软件进行求解。本文借助LINGO 11.0 软件，对算例进行求解，得出的应急资源调度方案如表5所示。

由表5 可以看出，在资源 R2、R4的总量不足的情况下，由于考虑了不同事故点的救援优先权，优先保证了事故点 G1、G3的需求。虽然事故点 G2、G4对资源 R2、R4的需求未得到全部满足，但总体而言，由于事故点 G1、G3的灾害损失较为严重，救援任务较为紧迫，优先保证其救援资源的需求能够确保整体救援效果的最大化。

5 结束语

以自然灾害导致的区域铁路网内的多处事故为例，对铁路应急资源调度问题进行了研究。充分考虑了事故救援初期，由于事故点灾情的随机性、不可预见性而导致的应急资源调配总量不能满足事故点的总需求这一现实矛盾，借鉴 TOPSIS 模型，通过设定 4个不同的评价指标，对不同事故点的救援优先权进行科学计算，确定了不同事故点的救援优先权。在此基础上，构建了铁路应急资源调度优化模型，并将反映事故点救援优先权的系数( αj，βj) 引入到模型中。利用该模型所求解得到的铁路应急资源调度方案，确保了优先权较高的事故点能够优先获得紧缺资源，最大程度减少灾害带来的损失。

表5 考虑事故点优先权的铁路应急资源调度方案

[1]陈喜春. 铁路危险货物运输应急管理[M]. 成都：西南交通大学出版社，2011.

[2]贾利民，秦 勇，程晓卿，等. 现代铁路应急管理[M]. 北京：科学出版社，2011.

[3]王富章. 铁路突发事件应急管理研究[M]. 北京：中国铁道出版社，2010.

[4]牛宏睿，李 平. 铁路突发事件单应急点多资源调度模型及仿真研究[C]// 第五届中国智能交通年会暨第六届国际节能与新能源汽车创新发展论坛. 第五届中国智能交通年会暨第六届国际节能与新能源汽车创新发展论坛优秀论文集(上册)——智能交通. 深圳：第五届中国智能交通年会暨第六届国际节能与新能源汽车创新发展论坛，2009：275-280.

[5]甘 勇，吕书林，李金旭，等. 考虑成本的多出救点多物资应急调度研究[J]. 中国安全科学学报，2011，21(9)：172-176.

[6]Jiuh-Biing Sheu. A Novel Dynamic Resource Allocation Model for Demand-responsive City Logistics Distribution Operations[J]. Transportation Research Part E，2006(42)：445-472.

[7]Jiuh-Biing Sheu. An Emergency Logistics Distribution Approach for Quick Response to Urgent Relief Demand in Disasters[J]. Transportation Research Part E，2007(43)：687-709.

[8]Jiuh-Biing Sheu. Dynamic Relief-demand Management for Emergency Logistics Operations Under Large-scale Disasters[J]. Transportation Research Part E，2010(46)：1-17.

[9]王艳辉，贾利民，秦 勇，等. 铁路应急管理理念与方法[M]. 北京：中国铁道出版社，2011.

[10]杨玉中，张 强，吴立云. 基于熵权的TOPSIS供应商选择方法[J]. 北京理工大学学报，2006，26(1)：31-35.

[11]Deng, H., Yeh, C.H., Willis, R.J. Inter-company Comparison Using Modified TOPSIS with Objective Weights[J]. Computers and Operations Research，2000，27 (10)：963–973.

[12]陈 雷，王延章. 基于熵权系数与TOPSIS集成评价决策方法的研究[J]. 控制与决策，2003，18(4)：456-459.

[13]杜 纲，岳松涛. 房地产开发投资决策的熵权系数优化模型[J]. 数理统计与管理，1999，18(1)：45-49.