铁路信息系统指标权重评价研究

吴华稳，王富章，陈志荣

（1.中国铁道科学研究院 电子计算技术研究所，北京 100081；2.广州铁路 ( 集团 ) 公司 计划统计处，广东 广州 510088）

随着铁路信息化程度的提升，衡量铁路信息系统指标权重的研究日益受到重视。很多学者对指标权重的评价方法进行了研究，如田军等用德尔菲法研究评价指标[1]，该方法虽然简单易行，有避免权威影响的好处，但存在不能相互交流意见，共同讨论问题，取得共识，缩短评价时间等缺点，亦有易受主观因素影响，不具备该方面知识的人的意见很难从总体意见中剔除。张灵莹采用模糊综合评价法研究指标权重[2]，该方法虽然通过精确的数字手段处理模糊的评价对象，但当指标集U较大，即指标集个数较多时，在权向量和为 1 的条件约束下，相对隶属度权重系数往往偏小，权向量与模糊矩阵R不匹配，结果会出现超模糊现象，分辨率很差，无法区分谁的隶属度更高，甚至造成评判失败。吴杰等采用数据包络分析方法 ( Data Envelopment Analysis，DEA ) 研究指标权重评价[3]，该方法排除了很多主观因素的影响，但无法对所有决策单元效率进行充分排序。祝凌曦等针对 DEA 方法的局限性，提出了改进 DEA 方法，克服了传统 DEA 方法无法确定有效决策单元优劣顺序的缺陷[4]。陈君等采用 BP 神经网络法对指标权重进行评价[5]，该方法有自身的缺陷，如其可以使权值收敛到某个值，但并不能保证其为误差平面的全局最小值；由于学习速率是固定的，因此网络的收敛速度慢，BP 算法需要较长的培训时间。本文在研究专家打分的基础上，采用改进的层次分析法 ( AHP )。由于 AHP 法受主观影响较大，研究先采用模糊聚类分析方法，在评估前通过聚类计算去掉专家打分偏差最大值，然后再用 AHP 法进行权重分析。

1 铁路信息系统指标权重评价体系

1.1 铁路信息系统评价指标体系

铁路信息系统指标体系是全面反映铁路运输生产实绩、运力资源运用情况、运输产品结构和分类，综合评价铁路运输生产、客货营销、经营管理的日常指标体系，涵盖铁路客运、货运、客车、货车、机车、调度、运输安全、经营收入等方面。

将各系统看做一个整体，构建铁路信息系统指标评价体系，各要素的指标集如下。

（1）系统层。系统层是铁路信息系统评价指标体系。

（2）要素层。要素层包括系统控制要素U1，人员控制要素U2，环境设备控制要素U3。

（3）指标层。指标层包括信息系统功能性r11，信息系统可靠性r12，信息系统实用性r13，信息系统效率r14；人员使用程度r21，人员技术业务能力r22，人员协作能力r23，人员认真程度r24；机器设备r31，网络带宽、网络环境r32，工作环境r33。

1.2 构建判断矩阵标度量

由专家对上述指标进行打分。打分方法为两两进行比较，设U＝{u1，u2，…，un}为评价因素集，uij表示ui对uj的相对重要性数值 (i，j＝1，2，…，n)，uij的取值如下。

（1）标度 1：表示两个因素相比，具有同样重要性。

（2）标度 3：表示两个因素相比，一个因素比另一个因素稍微重要。

（3）标度 5：表示两个因素相比，一个因素比另一个因素明显重要。

（4）标度 7：表示两个因素相比，一个因素比另一个因素强烈重要。

（5）标度 9：表示两个因素相比，一个因素比另一个因素极端重要。

（6）标度 2、4、6、8：表示上述两相邻判断的中值。

（7）倒数：因素i与j比较的判断为aij，则因素j与i比较的判断aji＝1 /aij。

2 基于聚类分析模糊综合赋权法

2.1 标准化打分数据

由于样本数据xi(xi∈X) 的特征指标 {xi1，xi2，…，xin}(i＝1，2，…，n) 是一个多维向量，每一种特征指标值的量纲不同，且数据不在 [ 0，1 ]闭区间上。因此，需要将原始数据标准化[6-7]。

原始数据的平均值 -xj为：

数据的标准差Sj为：

各数据的标准值为：

对x'ij进行极值标准化：

2.2 聚类分析

研究采用加权欧氏距离 k_means 算法。该算法的基本思想是在给出待测数据后，首先计算数据集中各属性的权值，在计算数据样本之间的相似度时使用加权欧式距离[8]，即

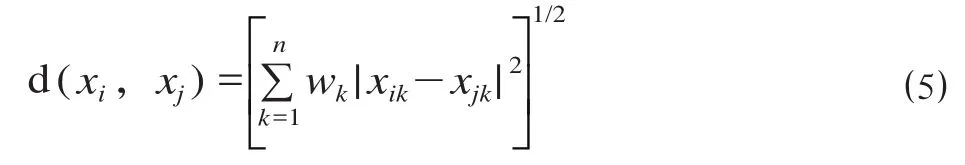
式中：wk(k＝1，2，…，p) 表示每个变量的权值。

算法输入：聚类个数k，以及包含n个数据对象的数据样本集U。

算法输出：满足方差最小标准的k个聚类。算法步骤如下。

步骤 1：从n个数据对象中任意选择k个对象作为初始聚类中心。

步骤 2：根据每个聚类中所有对象的均值，计算样本集中每个对象与这些均值的全权欧式距离，并根据最小加权欧式距离重心划分相应对象。

步骤 3：重新计算每个聚类的均值。

步骤 4：循环执行步骤 2 到步骤 3，直到每个聚类不再发生变化为止。

2.3 权重的确定

权重的计算采用 AHP 法，将评价权重指标进行两两对比打分，构造矩阵A[9-10]。

式中：aij＝1/aji(i≠j)，aij＝1 (i＝j)，aij的值由标度法确定。

（1）将矩阵A＝(aij)n×n的每一列向量进行归一化：

（2）对每一列归一化后的判断矩阵按行求和：

得到的W= [W1，W2，…，Wn]T即为所求的权向量。

（4）由矩阵理论可知其有最大特征根：

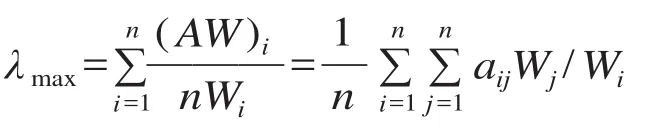
（5）一致性检验：CI= (λmax-n)/ (n- 1 )；CR=CI/RI。其中，CI是一致性指标；CR是一致性比率；RI是平均随机一致性指标。

3 应用举例

3.1 专家打分数据

以铁路信息系统为评估对象，采用综合评估法，邀请 6 位专家分别对系统控制要素中的功能性、可靠性、易使用性效率；人员控制因素中的人员使用熟练程度、业务能力、协作能力、认真程度；环境设备控制因素中的机器设备、网络环境、工作环境、培训环境等 12 个方面进行评估打分。评分采用两两指标比较方法，进行 9 级标度打分[11-12]。

首先，对要素层进行专家打分，系统控制要素用U1表示，人员控制要素用U2表示，环境设备控制要素用U3表示，采用两两比较方法进行打分。其中，U1—U2表示系统控制要素对人员控制要素的重要性。按照各要素判断重要性标度，要素层专家打分如表 1 所示，指标层专家打分如表 2 所示。

表1 要素层专家打分表

表2 指标层专家打分表

3.2 数据聚类处理

首先对系统控制要素U1的指标进行聚类分析，去掉偏差最大的专家打分。鉴于模糊聚类法的算法过程比较复杂且运算量较大，借助 SPSS17.0，通过计算机辅助实现模糊聚类处理。SPSS 根据聚类结果，自动生成相应的图形化界面，图 1 为条状分析图，其中白条越长表示偏离越大的组，可以看出，2 号和 5 号、1 号和 4 号专家评分最为接近，6 号专家评分偏差最大。

分析结果说明，6 号专家的评分受其主观因素的影响，与其他专家的评估结果发生了偏差，

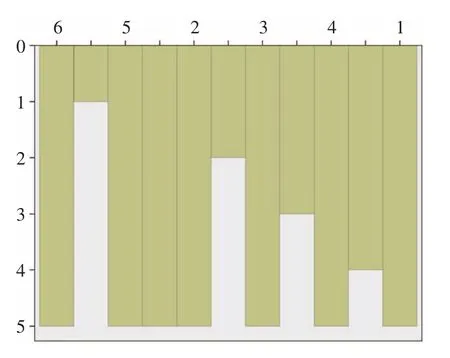
图1 聚类结果条状柱分析图

且偏差幅度较大，因而可以将其在此轮处理中剔除。同样，要素层专家打分进行聚类分析后得到专家 4 的打分受主观因素影响最大，因而在处理过程中将其剔除。对人员控制要素U2和环境设备控制要素U3进行聚类分析，分别得出在人员控制要素U2中 4 号专家与其他专家的打分偏差最大；U3中 5 号专家与其他专家的打分偏差最大。在评价处理中将这两位专家的评分剔除。要素层专家打分如表 3 所示，指标层专家打分如表 4 所示。从而得到处理后新的专家打分评价表。

3.3 数据模糊综合分析

运用层次分析法对上述均值进行权重分析，得到系统控制要素U1、人员控制要素U2和环境设备控制要素U3的权重数据。其中，矩阵平均一致性指标由大量试验数据确定，如表 5 所示。

3.3.1 全部专家打分后的权重数据

（1）要素层专家权重。系统控制要素U1、人员控制要素U2、环境设备控制要素U3的权重分别为：A= [ 0.604，0.268，0.128 ]T，λmax= 3.08；数据一致性效验为：CI= 0.04，CR= 0.069。

表3 要素层专家打分表

表4 指标层专家打分表

表5 RI 取值表

（2）系统控制要素U1。信息系统的功能性和信息系统的可靠性、信息系统的实用性和信息系统效率的权重分别为：WU1=[ 0.589，0.112，0.082，0.217 ]T，λU1max= 4.08；数据一致性效验为：CIU1= 0.027，CRU1= 0.030。

（3）人员控制要素U2。人员使用熟练程度、人员技术业务能力、人员协作能力、人员认真程度的权重分别为：WU2=[ 0.209，0.560，0.126，0.105]T，λU2max= 4.14；数据一致性效验为：CIU2= 0.047，CRU2= 0.052。

（4）环境设备控制要素U3。机器环境、网络带宽环境、工作环境的权重分别为：WU3= [ 0.591，0.178，0.231 ]T，λU3max= 3.08；数据一致性效验为：CIU3= 0.04，CRU3= 0.069。

3.3.2 去掉最大偏差后的专家打分权重数据

（1）要素层专家权重。系统控制要素U1、人员控制要素U2、环境设备控制要素U3的权重分别为：A= [ 0.609，0.259，0.132 ]T，λmax= 3.06；数据一致性效验为CI= 0.03，CR= 0.052。

（2）系统控制要素U1。信息系统的功能性、信息系统的可靠性、信息系统的实用性、信息系统效率的权重分别为：WU1= [0.569，0.103，0.089，0.239 ]T，λU1max= 4.07；数据一致性效验为：CIU1= 0.023，CRU1= 0.026。

（3）人员控制要素U2。人员使用熟练程度、人员技术业务能力、人员协作能力、人员认真程度的权重分别为：WU2= [0.209，0.567，0.118，0.106]T，λU2max= 4.08；数据一致性效验为：CIU2= 0.027，CRU2= 0.030。

（4）环境设备控制要素U3。机器环境、网络带宽环境、工作环境的权重分别为：WU3= [0.574，0.184，0.242]T，λU3max= 3.01；数据一致性效验为：CIU3= 0.005，CRU3= 0.008 6。

3.4 数据一致性校验

（1）一致性指标CI检验。对实例数据进行分析比较，CI前表示全部打分数据，即没有做聚类分析权重；CI后表示去掉偏差最大的数据，即进行聚类分析后的权重。

要素层权重：CI前= 0.04＞CI后= 0.03＞0

系统控制要素权重U1：CIU1前= 0.027＞CIU1后=0.023＞0

人员控制要素U2：CIU2前= 0.047＞CIU2后=0.027＞0

环境设备控制要素U3：CIU3前= 0.04＞CIU3后=0.005＞0

由于CI越接近 0，越有满意的一致性，每个权重层CI均为进行聚类后的权重更加接近 0，即去掉偏差最大的打分后的权重满意度更具有一致性。

（2）一致性比率CR检验。将实例数据进行分析比较。

要素层权重：CR后= 0.052＜CR前= 0.069＜0.1系统控制要素权重U1：CRU1后= 0.026＜CRU1前=0.030＜0.1

人员控制要素U2：CRU2后= 0.030＜CRU2前=0.052＜0.1

环境设备控制要素U3：CRU3后= 0.008 6＜CRU3前=0.069＜0.1

通过以上一致性CI和一致性比率CR检验可知，通过聚类后，即去掉偏差最大的打分后得到的权重更具备满意度一致性。

3.5 数据权重的综合评判

采用加权平均综合函数，根据铁路信息系统指标权重分析，得到各指标权重如下。

（1）系统控制要素的各指标权重：功能性0.347；可靠性 0.063；实用性 0.054；效率 0.146。

（2）人员控制要素的各指标权重：熟练程度0.054；业务能力 0.147；协作能力：0.031；认真程度 0.027。

（3）环境设备控制要素：机器环境 0.076；网络环境 0.024；工作环境 0.032。

4 结束语

将聚类理论应用到层次分析方法中，在层次分析法的框架下，对铁路信息系统指标权重进行系统评判，得到一系列有意义的结果。通过基于聚类理论的层次分析方法，可以更加客观、科学地评判铁路信息系统的指标权重，有效改进现有指标评价方法，降低纯粹采用专家打分法所带来的主观性问题，同时也增加了评估计算数据的准确性和有效性，进而降低了评估的难度，提高了评估的效率。该方法同样适用于其他领域的信息系统指标评估，具有较好的应用价值。

[1] 田 军，张朋柱，王刊良，等. 基于德尔菲法的专家意见集成模型研究[J]. 系统工程理论与实践，2004，12(1)：20-25.

[2] 张灵莹. 主观指标评价的模糊综合评价方法及应用[J]. 深圳大学学报，1998，12(1)：18-22.

[3] 吴 杰，石 琴. 基于DEA方法的多指标评价[J]. 系统工程与电子技术，2006，10(1)：22-26.

[4] 祝凌曦，肖雪梅，李 玮，等. 基于改进 DEA 法的铁路应急预案编制绩效评价方法研究[J]. 铁道学报，2011，4(33)：1-6.

[5] 陈 君，李聪颖，丁光明. 基于 BP 神经网络的高速公路交通安全评价[J]. 同济大学学报：自然科学版，2008，7(1)：28-31.

[6] 铁道部统计中心. 铁路统计信息化规划[J]. 中国铁路，2006，8(18)：12-15.

[7] 李夏苗，佘 勇，朱晓丽，等. 模糊聚类分析在铁路快运网络规划中的应用[J]. 中国铁道科学，2005，26(4)：124-129.

[8] 张忠林，曹志宇，李元韬. 基于加权欧式距离的 K_means算法研究[J]. 郑州大学学报：工学版，2010，31(1)：89-92.

[9] 毛邦燕，吴俊猛，喻洪平，等. 沪昆客专黄果树至北盘江段地址选线方案研究[J]. 铁道工程学报，2011，157(10)：19-24.

[10] 穆 瑞，张家泰. 基于灰色关联分析的层次综合评价[J]. 系统工程理论与实践，2008，12(10)：125-130.

[11] 付茂洺. 模糊综合分析在信息安全评估中的应用[J]. 西南交通大学学报，2010，45(3)：440-444.

[12] 高 阳，罗贤新，胡 颖. 基于判断矩阵的专家聚类赋权研究[J]. 系统工程与电子技术，2009，31(3)：593-596.