基于整流源的Buck变换器混沌现象研究
2013-11-22金爱娟王鸣翔李少龙
金爱娟, 王鸣翔, 夏 震, 李少龙
(1.上海理工大学 光电信息与计算机工程学院,上海 200093;2.上海现代光学系统重点实验室,上海 200093)
电力电子电路的本质是典型的非线性系统,存在分岔、混沌等动力学行为,影响了系统的稳定性[1-2].在工程实践中往往很难发现电路偏离正常状态而进入分岔和混沌现象的具体原因,而这个问题通过计算机仿真和计算比较容易发现产生问题的原因.在不同类型的电力电子电路中,DC-DC 变换器是研究得最多的.一般的文献都假设DC-DC变换器的输入端是直流稳压电源[3-4],但通常的实际情况并非如此.大多数情况下,DC-DC 变换器的输入端是经滤波后的整流源(整流后的直流电源),直流电压中将包含谐波,这种情况下所产生的分岔和混沌现象与理想直流电源供电状态下的有所不同.本文通过对模拟控制的Buck变换器在含不同电压幅值谐波分量的整流源供电下的非线性现象进行探讨,揭示其非线性动力学行为.
1 系统数学模型的建立
电流模式控制Buck变换器的原理图如图1所示.RS触发器的时钟脉冲信号频率固定,电感电流与参考电流相互比较后输入到触发器的R 端.在每个时钟周期的起始时刻,开关处于导通状态,当电感电流达到参考电流值时,开关关断.

图1 电流模式控制Buck变换器的原理图Fig.1 Schematic diagram of a current-mode controlled buck converter
电感电流i和电容电压vc设定为系统的状态变量.假设Vin是交流电经过整流器整流滤波后的纹波,令Vdc为平均直流分量,Vm为输入电压中所含谐波的电压幅值,n 为纹波电压中谐波的阶次.ω 为交流电源基波频率,θ为Buck变换器的初始开关瞬间与谐波电压分量过零瞬间的相位差.在导通和关断期间状态变量的关系可以通过线性微分方程组来描述.
开关导通期间

式 中,L 为电感;C 为电容;R 为电阻.
开关关断期间,在连续电流模式下
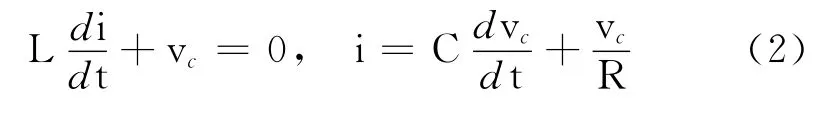
2 仿真结果
根据图1搭建MATLAB 电路仿真模型,参数取值为:参考电流iref=1A,电阻值R=10Ω,电感值L=0.4mH,电容值C=1mF,时钟频率为30kHz,输入电压直流分量的变化范围为10~20V.假设输入电压由一个单相全波整流器提供,含有幅值为直流电压分量的10%、频率为100Hz的谐波分量.因此,取n=2,Vm=0.1 Vdc,ω=314rad/s,且θ=0.
文献[5]提到,虽然仿真计算的算法精度能够达到要求,但是,这个精度引起的计算误差仍然导致仿真出来的分岔图和庞加莱截面图出现了异常的数据点.在文献[3]中提到,由于Buck 变换器工作模态的复杂性,它的分岔和混沌建模一直是一个困难的问题,由于系统对参数初始值的敏感性可能导致分析结果截然不同,结论的真实性也受到了质疑.为了减少误差,提高计算的准确度,本文在仿真计算中将精度提高到10-13,对仿真波形图进行分析,没有出现异常的数据点.在分岔混沌图中,分岔变量的步长取为0.1V,图2中的数据均是在电路状态稳定以后取出最后的500个数据点所形成的.
图2显示了以输入电压平均值作为变量的混沌图.为了观察输入电压谐波幅值的影响,在图2中,分别对含不同幅值谐波的整流源进行对比分析,在图2(b)、2(c)和2(d)中,仅仅改变其谐波幅值,其它参数不变.随着谐波幅值的升高,分岔结构没有本质的改变,只是状态空间的循环将变得更紧密,直到最后,它们会连接起来.对于其它参数的研究,只对10%的谐波含量进行研究,其它情况的分析和结论可以依此类推.

图2 以输入电压平均值为变量的混沌图Fig.2 Chaos diagrams with average DC input voltage as a variable
对于图2(a)以直流稳压电源作为输入的情况,一个标准的倍周期发生在16.5 V 处,其次是在13V和14V 处发生边界碰撞,导致系统从分岔向混沌状态的过渡.对于整流源供电的情况,混沌图如图2(b)、2(c)和2(d)所示.与图2(a)的混沌图不同的是,这里不能明显地看到过渡过程.
图2(b)的混沌图显示了某些区域内数据点的密集程度,当变换器的输入由整流器提供时,这个输入电压在每个周期内都有变化.因此,值得注意的是,如果适当地选择其它参数,分岔现象会发生在每一个输入电压周期内.由于在每一个纹波周期内存在固有的分岔,可以看到分岔图中数据点在某些区域里分布的密集程度不同,如在Vdc=15V 处.
图3是在输入电压值为12V 且含10%谐波时的一系列波形图.在图3(a)所示的庞加莱截面图中,呈现的是一种杂乱无章的混沌状态;图3(b)真实地反映出在各个时钟周期开始时刻的电感电流值;在图3(c)中,输入电压为直流稳压电源时,因为是工作在混沌状态下,所以电容电压相对于稳定状态来说纹波变大了.这与文献[6]提到的结论是一致的.在图3(c)中,输入电压为含10%谐波的整流源,电容电压值在稳定以后主要是由直流分量为7.876 713 369 233 95V和 接 近10%幅 值 的100 Hz谐波分量叠加而成的,谐波分量主要是由于输入纹波电压的谐波分量引起的;在图3(d)中可以看到电感电流在开关切换时刻的值,以及在不同区间开关的工作状态,上升曲线是开关导通阶段,下降曲线是开关关断的电流连续阶段,没有出现电流不连续阶段,它与图3(b)最大的区别就是反映出电感电流等于参考电流值的时刻.图3(a)和3(c)都是由离散的数据点构成的,而在图3(b)和3(d)中,为了清楚地显示各个状态的时间关系,将各个数据点用直线进行连接.实际上,电感电流波形的时域图与图3(d)是基本一致的,所以,没有重复给出.
图4是在输入电压值为14V 且含10%谐波时的一系列波形图.在图4(a)中,电感电流和电容电压的庞加莱截面图是两个形状相似的环形结构.系统处于混沌状态时出现的相图环形或其它结构的性质有可能完全相同,也有可能不同,这取决于系统参数的变化.环形或其它结构的数量以及其所包含的离散数据点的数量,由系统周期性以及开关频率和谐波频率的比例决定.图4(c)的电容电压在过渡过程中存在超调量,电容电压值在稳定以后主要 是由直流分量为7.14752991112792V和接近10%幅值的100 Hz谐波分量叠加而成的,它比图3(c)的直流分量略小.由图3(b)、3(d)结合图2(b)可以看到,电感电流的采样值分布在上下两个局部范围内,在中间部分是空缺的.

图3 电压值为12V 且含10%谐波时的波形图Fig.3 Diagrams for 12Vinput DC source with 10%ripple content

图4 电压值为14V 且含10%谐波时的波形图Fig.4 Diagrams for 14Vinput DC source with 10%ripple content
图5是在输入电压值为18V 且含10%谐波时的一系列波形图.在图5(a)中,电感电流和电容电压的庞加莱截面图是一个椭圆形结构.由图5(b)、5(d)结合图2(b)可以看到,电感电流的采样值的直流分量为0.628 119 363 567 29A 和约6%幅值的100Hz谐波分量叠加而成的.从图5(b)、图4(b)、图3(b)和图2(b)、2(c)、2(d)上来看,图5(b)的变化频率与输入电压谐波分量的频率是相同的,与其说它是一种混沌状态,不如说是输入电压谐波分量在输出采样电流上的反映,而且在图2(b)、2(c)、2(d)上对应于输入电压18V 的输出采样电流的范围是与输入电压谐波分量的幅值成正比例关系的.图5(c)的电容电压在过渡过程中存在超调量,电容电压值在稳定以后是由直流分量为8.168 141 045 188 11V和接近10%幅值的100Hz谐波分量叠加而成的,它比图3(c)的直流分量略大.所以,电流模式控制Buck变换器的负载端电压及其电流都是随着输入电压参数的变化而变化的.然而,输入电压的直流分量不能太低,否则电路无法正常工作.

图5 电压值为18V 且含10%谐波时的波形图Fig.5 Diagrams for 18Vinput DC source with 10%ripple content
3 结 论
研究了以由整流器供电的纹波电压源替代理想直流电压源的电流模式控制Buck变换器的分岔与混沌现象.在这两种输入情况下,所观察到的现象存在明显的区别.以整流源供电时,图表中的分岔过渡并不能很清晰地看出.输入电压中存在的谐波分量导致电容电压和采样电感电流包含了相同频率的谐波分量,电容电压谐波分量的幅值具有与输入电压中谐波分量幅值相当的比例,而采样电感电流谐波分量的幅值与输入电压中谐波分量幅值各自所占的比例不相同,但是,具有正比例关系.而且输入电压中存在的谐波分量还将周期性的轨迹变为锁相轨迹,而庞加莱截面图也由包含点变成了包含环形或某个结构.本文虽然假设整流源的纹波电压仅含有一种特定的谐波分量,但是其它的谐波分量也可以依此类推.
[1]王春芳,王开艳,李强.Buck变换器仿真模型及分岔与混沌研究[J].系统仿真学报,2007,19(24):5824-5826.
[2]Yao Y,Fassinou F,Hu T.Stability and robust regulation of battery driven boost converter with simple feedback[J].IEEE Transactions on Power Electronics,2011,26(9):2614-2616.
[3]张波,曲颖.BUCK DC/DC变换器分岔和混沌的精确离散模型及实验研究[J].中国电机工程学报,2003,23(12):99-103.
[4]Wang Yuanbin.Research on chaos in switching DC-DC converters[C]∥Intelligent Computation Technology and Automation,2009,3:91-94.
[5]朱雪丰,徐冬亮,舒秀发,等.BUCK 转换器中的分岔与混沌研究[J].系统仿 真 学 报,2007,19(15):3387-3389.
[6]卢伟国,周雒维,罗全明.电压模式BUCK变换器输出延迟反馈混沌控制[J].物理学报,2007,56(10):5648-5654.
