基于在线定子电流优化的IPMSM 驱动系统控制
2013-11-22周亚男李红梅刘子豪华新强
周亚男,李红梅,刘子豪,华新强
(合肥工业大学,安徽合肥230009)
0 引 言
永磁同步电机(以下简称PMSM)具有高效率、高功率密度、较高的弱磁扩速能力与安全可靠性,在电动汽车领域获得了广泛应用。电动汽车PMSM驱动系统通常采用基于磁场定向的最大转矩电流比控制(以下简称MTPA)与弱磁控制,实现电驱动系统在宽调速范围内的高效运行。
由于电动汽车运行工况的复杂性,电驱动系统中的PMSM 易出现磁路饱和与交叉饱和,导致PMSM 的电感参数与定子电流之间呈现非线性特性,而且其电感参数值在较大范围内变化。若不考虑PMSM 电感参数的变化,势必导致电驱动系统运行时电机转矩输出能力下降和系统效率降低,甚至出现恒功率运行时的系统失稳现象,导致故障停机。为此,计及磁路饱和及交叉饱和引起的电感参数变化条件下,实现宽调速范围内PMSM 磁场定向控制系统的MTPA 控制和弱磁控制已获得国内外学者的研究关注,并提出了若干可供借鉴的解决方案。
文献[1]基于MTPA 指令与负d 轴电流反馈实现了PMSM 的宽调速范围运行控制,但该方案的技术不足在于电机深度弱磁时,如参数设置不合理会导致电流调节器饱和而导致系统失控。文献[2]改进了此方案,针对具有无限扩速比的PMSM,通过对d 轴电流限幅,并增加q 轴电流弱磁补偿,保证了PMSM 在深度弱磁时系统的稳定性。上述方案均是通过电压环反馈获得d 轴去磁电流,对PMSM 磁路饱和引起的电感参数变化具有较强的抗扰性,但是由于电压环的引入,系统高转速运行的稳定性与快速响应性仍然面临挑战。
文献[3]忽略d 轴磁路饱和与交叉饱和,仅考虑q 轴磁路饱和,采用拉格朗日乘数法,分别就最小损耗控制与弱磁控制,通过对高次极小值项的忽略和泰勒级数近似方法,获得最小损耗控制与弱磁控制时定子电流指令近似解析表达式。在实时控制时,基于指令转矩、实际转速和定子电流指令实现内嵌式永磁同步电机(以下简称IPMSM)的磁场定向控制。此方案的不足在于其仅考虑q 轴磁路饱和现象,且对q 轴电感进行线性化拟合实现简化分析计算,仅能获得定子电流最优指令的近似解析表达式。
文献[4-6]研究了计及磁路饱和与交叉饱和后IPMSM 的控制,基于离线计算定子电流的最优值,在实时控制时,采用电流指令表,获取最优定子电流指令,而且该控制系统增加了基于电压反馈的定子磁链观测器,通过指令转矩与观测到的定子磁链来查表获取定子电流指令。
上述方法虽然可以获得定子电流的近似最优值,但是在离线计算时,由于需要考虑IPMSM 电感参数的变化,求解过程会涉及大量的迭代、复杂的计算步骤,获取最优定子电流指令较为复杂,如更换不同的被控电机,需要重新计算电流指令表,耗费大量的时间与精力。
文献[7]提出了考虑磁路饱和及交叉饱和后,IPMSM 驱动系统损耗最小控制时的最优定子电流指令在线计算方法,但是对于电动汽车应用场合,仍需要解决电驱动系统弱磁控制时的定子电流指令的在线计算及MTPA 控制及弱磁控制的平滑切换等问题。
为了避免大量、复杂的计算过程,同时在线获取IPMSM 驱动系统MTPA 控制与弱磁控制的定子电流指令的近似最优值,而且实现MTPA 控制与弱磁控制的平滑切换,本文提出了基于在线定子电流优化的IPMSM 磁场定向控制系统的MTPA 控制及弱磁控制方案,旨在实现计及磁路饱和及交叉饱和影响后的IPMSM 驱动系统在宽调速范围内的高效稳定运行。
1 考虑磁路饱和及交叉饱和后的IPMSM 数学模型
在同步速旋转的坐标系下,端电压约束方程:
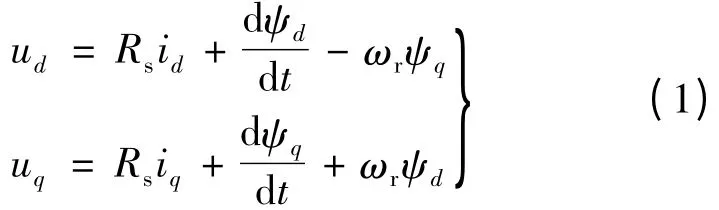
式中:ud、ud为定子d、q 轴电压;id、id为定子d、q 轴电流;ψd、ψd为定子d、q 轴磁链;ωr为转子电角速度;Rs为定子绕组电阻。
由于PMSM 磁路及铁磁材料的导磁特性是非线性的,因此,考虑磁路饱和及交叉饱和影响时,PMSM 定子d、q 轴电感与定子d、q 轴电流是非线性函数关系[],假设永磁体产生的磁链恒定,则定子磁链的d、q 轴分量表达式:
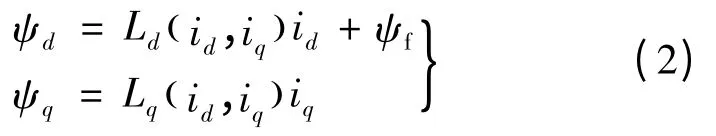
式中:Ld、Ld为定子d、q 轴同步电感;ψf表示永磁体基波磁链。
将式(2)代入式(1),考虑磁路饱和及交叉饱和后的IPMSM 电压约束方程:
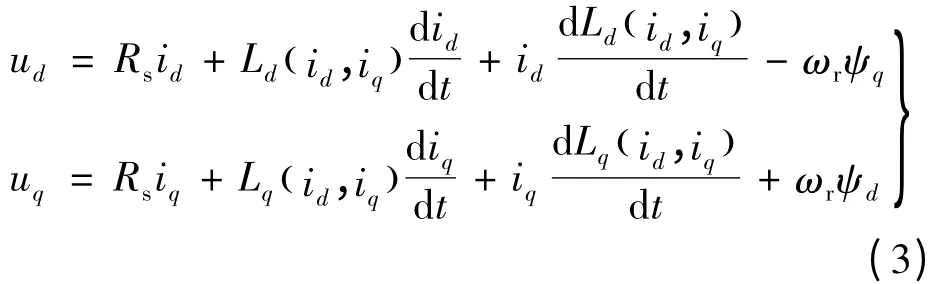
电磁转矩方程:
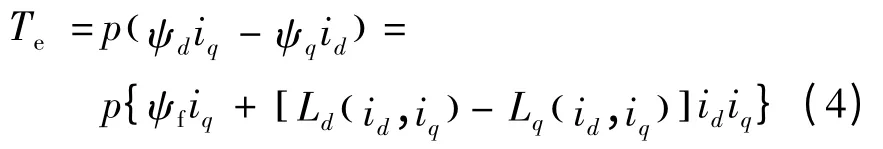
式中:Te为电磁转矩,np为极对数。
机电运动方程:
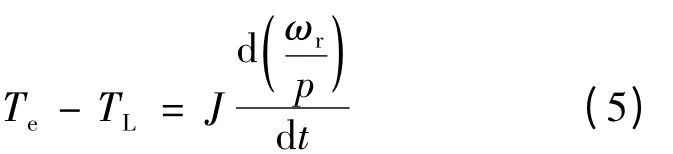
式中:TL为负载转矩,J 为转动惯量。
联立式(3)~式(5),选取id、iq、ωr为状态变量,构成计及磁路饱和及交叉饱和后的IPMSM 数学模型。
2 基于磁场定向的IPMSM 驱动系统MTPA控制和弱磁控制
2.1 系统结构
考虑磁路饱和及交叉饱和后IPMSM 驱动系统结构框图如图1 所示,系统采用转速外环和电流内环的双闭环结构,虚线框内各功能由处理器模块完成。转速外环输出经限幅后,生成定子电流指令i*n,考虑磁路饱和及交叉饱和后的电流指令变换器根据i*n、Udc、实时d、q 轴定子电流和实时转速获得定子d、q 轴电流指令最优值,实现磁场定向的IPMSM 系统在计及磁路饱和及交叉饱和影响后的MTPA 控制与弱磁控制。
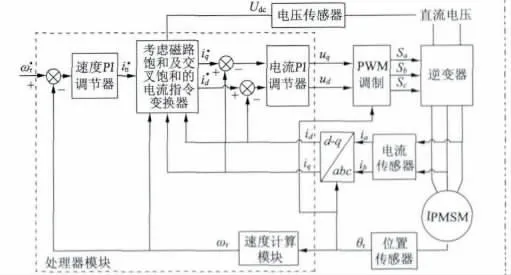
图1 考虑磁路饱和及交叉饱和后PMSM 驱动系统结构框图
定子电流指令变换器结构如图2 所示,主要由定子电流指令组生成、MTPA 判断、弱磁判断与最优定子电流指令生成四部分组成。
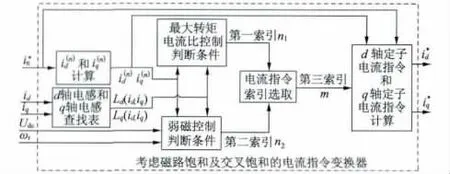
图2 考虑磁路饱和及交叉饱和的电流指令变换器结构框图
2.2 定子电流指令组
定义PMSM 定子电流矢量is与转子同步旋转坐标系下q 轴夹角为β角,选取β 角的大小分别为,如表1 所示,并给9 个β 角分配索引n,得到9 组d、q轴定子电流指令组,如图3 所示。
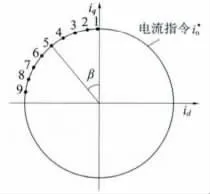
图3 定子电流指令组获取
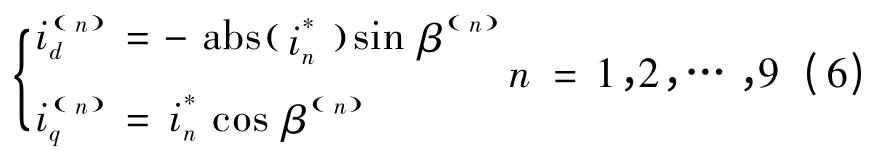

表1 定子电流指令组
2.3 MTPA 指令判断条件
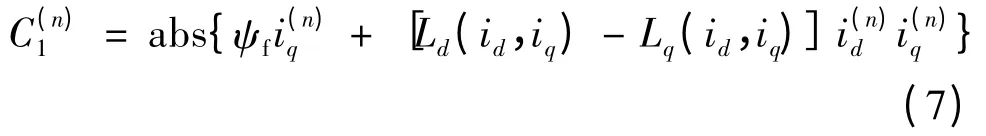

图4 MTPA 指令判断条件
2.4 弱磁指令判断条件
弱磁控制判断条件C2(n)为:
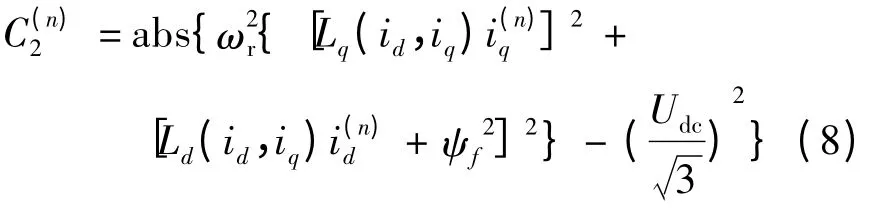
C2(n)中最小值所对应的索引作为第二索引n2。

图5 弱磁指令判断条件
2.5 MTPA 控制与弱磁控制的平滑切换及定子电流指令的自动生成
对于IPMSM 驱动系统,其MTPA 控制与弱磁控制间的切换大都采用固定转折速度或者比较d 轴定子电流指令的大小来实现,前者降低系统性能,后者计算量较大,因此在满足MTPA 控制与弱磁控制动态平滑切换条件下,尚需简化切换策略。为此,本文提出通过比较第一索引n1与第二索引n2的值大小,选取较大值作为第三索引m,实现MTPA 控制和弱磁控制之间的平滑切换,其流程图如图6 所示。
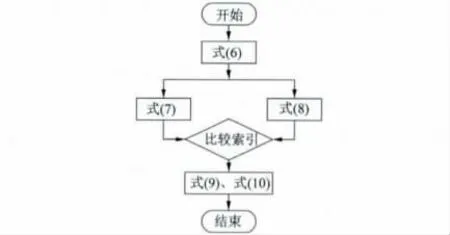
图6 MTPA 控制与弱磁控制平滑切换流程图
选取第三索引m 及相邻索引m-1 和m + 1 所对应的d、q 轴定子电流指令组和以及相对应的MTPA 控制判断条件或弱磁控制判断条件,利用式(9)自动获得d、q 轴定子电流指令
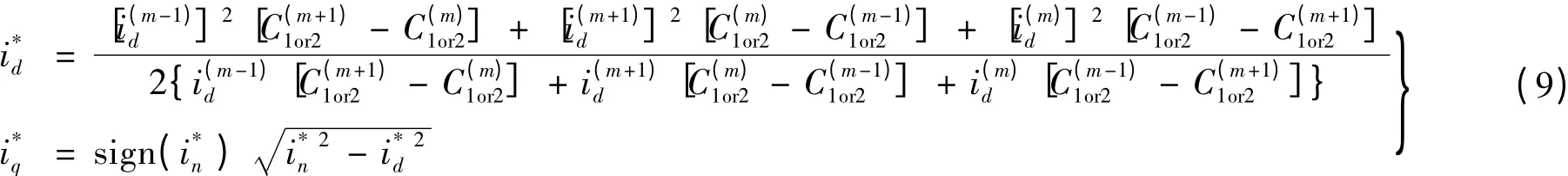
若m = 1 或m = 9,则d 轴定子电流指令i*d和q轴定子电流指令i*q按照式(10)获得:
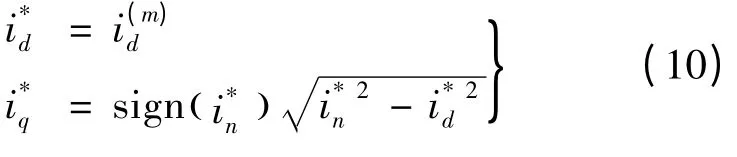
3 系统仿真研究
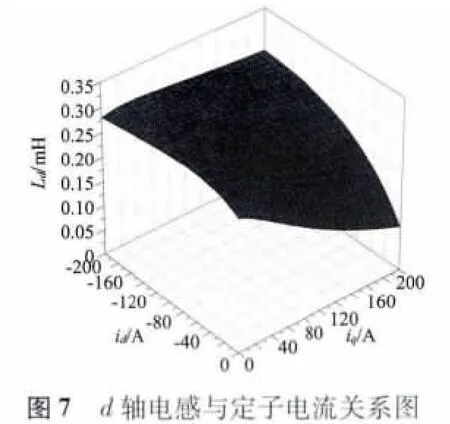
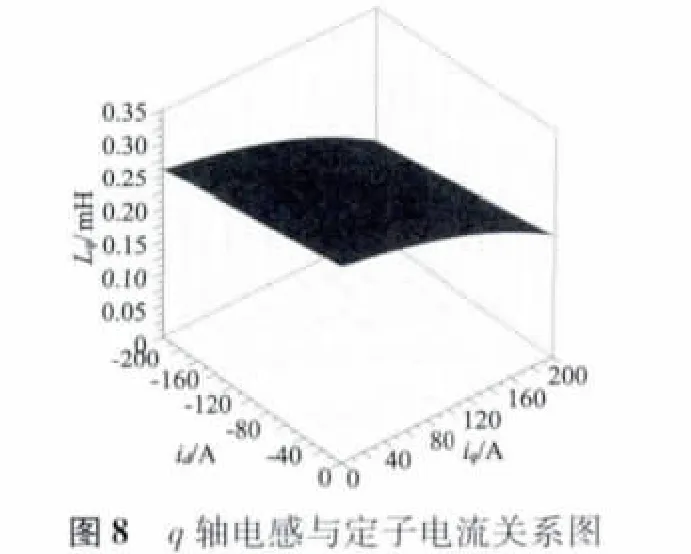
采用MATLAB Simulink 与C-MEX S-Function 建立考虑磁路饱和及交叉饱和后的IPMSM 驱动系统的仿真模型,驱动电机选用额定功率18 kW、峰值功率42 kW 的IPMSM,Ld、Lq与定子电流之间关系如图7 和图8 所示,直流母线电压Udc为312 V,SVPWM 开关频率9.1 kHz,仿真采用变步长。
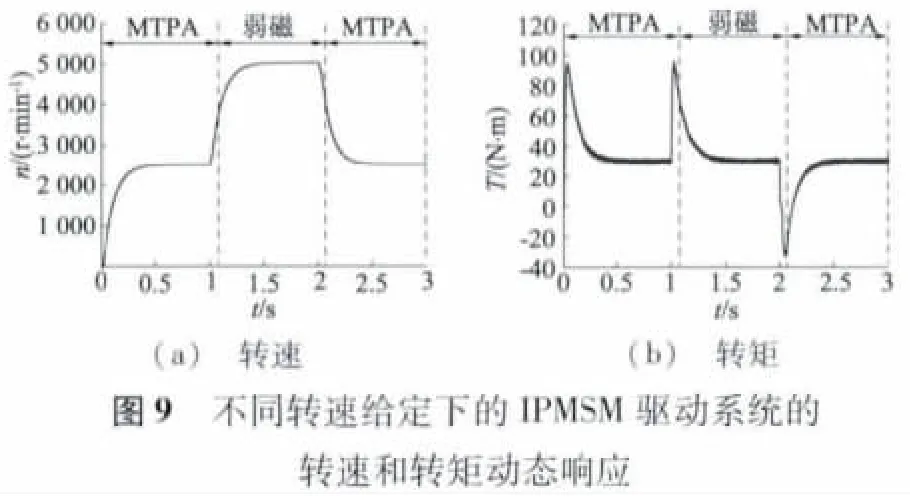
系统采用转速外环、电流内环的双闭环控制,负载30 N · m ,给 定 转 速2500 r / min ,1 s 时 加 速 至5 000 r/min,在2 s 时减速至2 500 r/min,系统的转速与转矩动态响应如图9 所示,虚线表示MPTA 控制与弱磁控制的切换点。从图中可见,所设计的控制策略能够实现宽调速范围内的MTPA 控制、弱磁控制以及两者之间的平滑切换,系统具有良好的转速动态性能。
系统采用单电流闭环控制,给定电流指令i*n为210 A,电流指令斜坡0.3 s,负载60 N·m,持续加速0.4 s,所提出的基于在线定子电流优化的IPMSM驱动控制系统与不计磁路饱和及交叉饱和影响的定IPMSM 参数的驱动控制系统[9]在控制系统参数均相同的情况下,其电机转速与转矩动态性能比较如图10 所示,图中虚线表示MTPA 控制与弱磁控制的切换点。系统仿真结果表明,所建议的IPMSM 驱动系统控制方案在系统弱磁控制运行时能够输出更高的电磁转矩,且扩展了系统的恒转矩区。
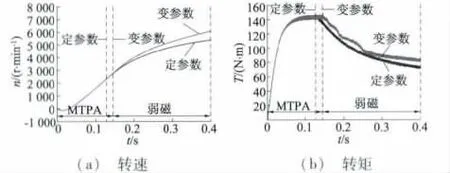
图10 IPMSM 驱动系统不同控制策略下的转速和转矩动态响应
4 结 语
本文计及IPMSM 磁路饱和与交叉饱和影响后,为了提高IPMSM 驱动系统在宽调速范围的运行性能,避免离线计算定子电流指令表的复杂过程,给出了基于在线定子电流优化的IPMSM 驱动系统的新型控制方案,该方案能够自动在线获取定子电流指令的最优值,实现IPMSM 驱动系统的MTPA 控制、弱磁控制及两者间平滑切换。较之不计电机磁路饱和与交叉饱和影响的IPMSM 驱动系统的控制方案,本文建议的IPMSM 驱动系统控制方案不仅具有良好的动态和静态性能,而且能够充分挖掘IPMSM 的转矩潜能,实现电驱动系统在宽调速范围内的高效节能运行。
[1] Jang-Mok K,Seung-Ki S.Speed control of interior permanent magnet synchronous motor drive for the flux weakening operation[J].IEEE Transactions on Industry Applications,1997,33:43 -48.
[2] 朱磊,温旭辉,赵峰,等.永磁同步电机弱磁失控机制及其应对策略研究[J].中国电机工程学报,2011(31):67-72.
[3] J Lee,K Nam,S Choi,et al.Loss-minimizing control of PMSM with the use of polynomial approximations[J].IEEE Transactions on Power Electronics,2009(24):1071-1082.
[4] H W de Kock,A J Rix,M J Kamper.Optimal torque control of synchronous machines based on finite-element analysis [J].IEEE Transactions on Industrial Electronics,2010(57):413-419.
[5] Cheng B,Tesch T R.Torque feedforward control technique for permanent-magnet synchronous motors [J].IEEE Transactions on Industrial Electronics,2010(57):969-974.
[6] Lenke R U,De Doncker R W,Kwak M S,et al.Field weakening control of interior permanent magnet machine using improved current interpolation technique [C]/ /2006 IEEE Power Electronics Specialists Conference.IEEE,2006:954-958.
[7] Adawey J B,Yamamoto S,Kano T,et al.Maximum efficiency drives of interior permanent magnet synchronous motor considering iron loss and cross-magnetic saturation[C]/ /International Conference on Electrical Machines and Systems.2009:1-6.
[8] Stumberger B,Stumberger G,Dolinar D,et al.Evaluation of saturation and cross-magnetization effects in interior permanent-magnet synchronous motor [J].IEEE Transactions on Industry Applications,2003(39):1264-1271.
[9] Shinnaka S.A new current control method for energy-efficient/wide-speed-range drive of permanent magnet synchronous motor[J].Electrical Engineering in Japan.2007(161):66-77.